Hostname: page-component-7dd5485656-hw7sx Total loading time: 0 Render date: 2025-10-31T05:39:42.310Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SETS OF PP-GENERATORS OF FINITE GROUPS

Part of: Special aspects of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  14 October 2014

JAN KREMPA  and
AGNIESZKA STOCKA
JAN KREMPA
Affiliation:
Institute of Mathematics, University of Warsaw, Banacha 2, 02-097 Warszawa, Poland email jkrempa@mimuw.edu.pl
AGNIESZKA STOCKA*
Affiliation:
Institute of Mathematics, University of Białystok, Akademicka 2, 15-267 Białystok, Poland email stocka@math.uwb.edu.pl
*
✉stocka@math.uwb.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classes of finite groups with minimal sets of generators of fixed cardinalities, named 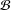${\mathcal{B}}$-groups, and groups with the basis property, in which every subgroup is a 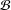${\mathcal{B}}$-group, contain only 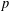$p$-groups and some 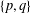$\{p,q\}$-groups. Moreover, abelian 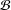${\mathcal{B}}$-groups are exactly 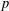$p$-groups. If only generators of prime power orders are considered, then an analogue of property 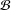${\mathcal{B}}$ is denoted by 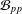${\mathcal{B}}_{pp}$ and an analogue of the basis property is called the pp-basis property. These classes are larger and contain all nilpotent groups and some cyclic 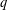$q$-extensions of 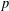$p$-groups. In this paper we characterise all finite groups with the pp-basis property as products of 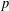$p$-groups and precisely described $\{p,q\}$-groups.

Keywords

finite groupgenerating setindependent setsoluble group

MSC classification

Primary: 20F05: Generators, relations, and presentations
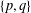Secondary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks 20D60: Arithmetic and combinatorial problems

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 2 , April 2015 , pp. 241 - 249
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Aljouiee, A. and Alrusaini, F., ‘Matroid groups and basis property’, Int. J. Algebra 4 (2010), 535–540.Google Scholar
Apisa, P. and Klopsch, B., ‘A generalization of the Burnside basis theorem’, J. Algebra 400 (2014), 8–16.Google Scholar
Delgado, A. L. and Wu, Y.-F., ‘On locally finite groups in which every element has prime power order’, Illinois J. Math. 46(3) (2002), 885–891.Google Scholar
Gorenstein, D., Finite Groups, 2nd edn (Chelsea, New York, 1980).Google Scholar
Krempa, J. and Stocka, A., ‘On some invariants of finite groups’, Int. J. Group Theory 2(1) (2013), 109–115.Google Scholar
Krempa, J. and Stocka, A., ‘On some sets of generators of finite groups’, J. Algebra 405 (2014), 122–134.CrossRefGoogle Scholar
Krempa, J. and Stocka, A., ‘Corrigendum to ‘On some sets of generators of finite groups’’, J. Algebra, 408 (2014), 61–62.Google Scholar
Lucchini, A., ‘The largest size of a minimal generating set of a finite group’, Arch. Math. 101 (2013), 1–8.Google Scholar
McDougall-Bagnall, J. and Quick, M., ‘Groups with the basis property’, J. Algebra 346 (2011), 332–339.CrossRefGoogle Scholar
Robinson, D. J. S., A Course in the Theory of Groups, 2nd edn (Springer, New York, 1996).Google Scholar
Scapellato, R. and Verardi, L., ‘Groupes finis qui jouissent d’une propriété analogue au théorème des bases de Burnside’, Boll. Unione Mat. Ital. A (7) 5 (1991), 187–194.Google Scholar