Refine search
Actions for selected content:
11 results
A REMARK ON THE N-INVARIANT GEOMETRY OF BOUNDED HOMOGENEOUS DOMAINS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 23 May 2024, pp. 928-937
- Print publication:
- December 2024
-
- Article
- Export citation
Weighted nonlinear flag manifolds as coadjoint orbits
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 1664-1694
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximum likelihood estimation for tensor normal models via castling transforms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 01 July 2022, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symplectic quotients have symplectic singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 3 / March 2020
- Published online by Cambridge University Press:
- 31 January 2020, pp. 613-646
- Print publication:
- March 2020
-
- Article
- Export citation
II - Sheaves of Monoids
-
- Book:
- Lectures on Logarithmic Algebraic Geometry
- Published online:
- 02 November 2018
- Print publication:
- 08 November 2018, pp 184-269
-
- Chapter
- Export citation
SYMPLECTIC STRUCTURES ON STATISTICAL MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 15 June 2011, pp. 371-384
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Stratifications with respect to actions of real reductive groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 163-185
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
Decomposition of Marsden–Weinstein Reductions for Representations of Quivers
-
- Journal:
- Compositio Mathematica / Volume 130 / Issue 2 / January 2002
- Published online by Cambridge University Press:
- 04 December 2007, pp. 225-239
- Print publication:
- January 2002
-
- Article
-
- You have access
- Export citation
Geometry of the Moment Map for Representations of Quivers
-
- Journal:
- Compositio Mathematica / Volume 126 / Issue 3 / May 2001
- Published online by Cambridge University Press:
- 04 December 2007, pp. 257-293
- Print publication:
- May 2001
-
- Article
-
- You have access
- Export citation
Deformation Quantization of Symplectic Fibrations
-
- Journal:
- Compositio Mathematica / Volume 123 / Issue 2 / September 2000
- Published online by Cambridge University Press:
- 04 December 2007, pp. 131-165
- Print publication:
- September 2000
-
- Article
-
- You have access
- Export citation
Formules de localisation en cohomologie equivariante
-
- Journal:
- Compositio Mathematica / Volume 117 / Issue 3 / July 1999
- Published online by Cambridge University Press:
- 04 December 2007, pp. 243-293
- Print publication:
- July 1999
-
- Article
-
- You have access
- Export citation
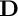
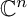
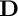
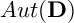
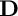
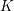
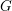
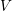
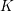

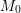
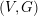


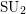
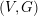
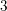
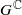 and that with respect to a compatible maximal compact subgroup
and that with respect to a compatible maximal compact subgroup 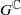 the action on
the action on 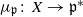 where
where 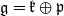 is a Cartan decomposition of
is a Cartan decomposition of 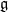 . We obtain a Morse-like function
. We obtain a Morse-like function 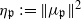 on
on 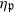 are various sets of semistable points which we study in great detail. In particular, we have
are various sets of semistable points which we study in great detail. In particular, we have 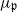 is proper, the pre-strata form a decomposition of
is proper, the pre-strata form a decomposition of 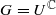 and
and 