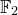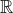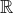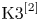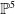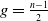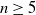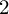Refine search
Actions for selected content:
40 results
Hyperbolic geometry and real moduli of five points on the line
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
11 - Recent Developments on Compactifications of Stacks of Shtukas
-
-
- Book:
- Moduli, Motives and Bundles
- Published online:
- 31 October 2025
- Print publication:
- 20 November 2025, pp 423-446
-
- Chapter
- Export citation
A flag version of Beilinson–Drinfeld Grassmannian for surfaces
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Moduli, Motives and Bundles
- New Trends in Algebraic Geometry
-
- Published online:
- 31 October 2025
- Print publication:
- 20 November 2025
Moduli space theory for complete, constant Q-curvature metrics on finitely punctured spheres
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 October 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODULI SPACES OF SLOPE-SEMISTABLE SHEAVES WITH REFLEXIVE SESHADRI GRADUATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 22 August 2025, pp. 728-746
- Print publication:
- December 2025
-
- Article
- Export citation
Maximal real varieties from moduli constructions
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The coarse geometry of hexagon decomposition graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Towards a modular construction of OG10
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 08 November 2024, pp. 2496-2529
- Print publication:
- October 2024
-
- Article
- Export citation
Geometric aspects on Humbert-Edge curves of type 5, Kummer surfaces and hyperelliptic curves of genus 2
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 25 July 2023, pp. 612-624
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived categories of hyper-Kähler manifolds: extended Mukai vector and integral structure
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 109-152
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
13 - Dimensional Reduction and T-Duality
- from Part IV - Outlook
-
- Book:
- A Short Introduction to String Theory
- Published online:
- 31 March 2022
- Print publication:
- 07 April 2022, pp 155-214
-
- Chapter
- Export citation
REPRESENTATION VARIETIES OF ALGEBRAS WITH NODES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 2215-2245
- Print publication:
- November 2022
-
- Article
- Export citation
LOCALIZATION BY
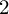 $2$-PERIODIC COMPLEXES AND VIRTUAL STRUCTURE SHEAVES
$2$-PERIODIC COMPLEXES AND VIRTUAL STRUCTURE SHEAVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 December 2020, pp. 1477-1506
- Print publication:
- September 2022
-
- Article
- Export citation
Instanton sheaves and representations of quivers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 984-1004
-
- Article
- Export citation
Lecture 1 - Closed Holomorphic Curves in Symplectic 4-Manifolds
-
- Book:
- Lectures on Contact 3-Manifolds, Holomorphic Curves and Intersection Theory
- Published online:
- 06 March 2020
- Print publication:
- 26 March 2020, pp 11-25
-
- Chapter
- Export citation
Introduction: Motivation
-
- Book:
- Lectures on Contact 3-Manifolds, Holomorphic Curves and Intersection Theory
- Published online:
- 06 March 2020
- Print publication:
- 26 March 2020, pp 1-10
-
- Chapter
- Export citation
Appendix A - Properties of Pseudoholomorphic Curves
-
- Book:
- Lectures on Contact 3-Manifolds, Holomorphic Curves and Intersection Theory
- Published online:
- 06 March 2020
- Print publication:
- 26 March 2020, pp 94-107
-
- Chapter
- Export citation
7 - Bergman Tau-Function: From Einstein Equations and Dubrovin-Frobenius Manifolds to Geometry of Moduli Spaces
-
-
- Book:
- Integrable Systems and Algebraic Geometry
- Published online:
- 19 March 2020
- Print publication:
- 02 March 2020, pp 215-287
-
- Chapter
- Export citation
Dynamical degrees of Hurwitz correspondences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1968-1990
- Print publication:
- July 2020
-
- Article
- Export citation