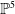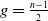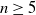1. Introduction
W.L. Edge began the study of Humbert’s curves in [
Reference Edge5
]; such curves are defined as canonical curves in
![]() ${\mathbb{P}}^4$
that are the complete intersection of three diagonal quadrics. A natural generalization of Humbert’s curve was later introduced by Edge in [
Reference Edge7
]: irreducible, non-degenerated, and non-singular curves on
${\mathbb{P}}^4$
that are the complete intersection of three diagonal quadrics. A natural generalization of Humbert’s curve was later introduced by Edge in [
Reference Edge7
]: irreducible, non-degenerated, and non-singular curves on
![]() ${\mathbb{P}}^n$
that are the complete intersection of
${\mathbb{P}}^n$
that are the complete intersection of
![]() $n-1$
diagonal quadrics. One important feature of Humbert-Edge curves of type
$n-1$
diagonal quadrics. One important feature of Humbert-Edge curves of type
![]() $n$
noted by Edge in [
Reference Edge7
] is that each one admits a normal form. Indeed, we can assume that the
$n$
noted by Edge in [
Reference Edge7
] is that each one admits a normal form. Indeed, we can assume that the
![]() $n-1$
quadrics in
$n-1$
quadrics in
![]() ${\mathbb{P}}^n$
are given by
${\mathbb{P}}^n$
are given by
where
![]() $a_j\in \mathbb{C}$
for all
$a_j\in \mathbb{C}$
for all
![]() $j\in \{0,\dots,n\}$
and
$j\in \{0,\dots,n\}$
and
![]() $a_j\neq a_k$
if
$a_j\neq a_k$
if
![]() $j\neq k$
, and here,
$j\neq k$
, and here,
![]() $a_j^i$
denotes the
$a_j^i$
denotes the
![]() $i$
th power of the
$i$
th power of the
![]() $a_j$
. We say that a curve satisfying this conditions is a Humbert-Edge curve of type
$a_j$
. We say that a curve satisfying this conditions is a Humbert-Edge curve of type
![]() $n$
. Note that in the case of a Humbert’s curve
$n$
. Note that in the case of a Humbert’s curve
![]() $X$
, i.e. when
$X$
, i.e. when
![]() $n=4$
, this form of the equations implies directly that
$n=4$
, this form of the equations implies directly that
![]() $X$
is contained in a degree four Del Pezzo surface.
$X$
is contained in a degree four Del Pezzo surface.
The Humbert-Edge curves of type
![]() $n$
for
$n$
for
![]() $n\gt 4$
has been studied in just a few works. Carocca, González-Aguilera, Hidalgo, and Rodríguez studied in [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
] the Humbert-Edge curves from the point of view of uniformization and Klenian groups. Using a suitable form of the quadrics, Hidalgo presented in [
Reference Gonzalez-Dorrego11
] and [
Reference Hidalgo12
] a family of Humbert-Edge curves of type 5 whose fields of moduli are contained in
$n\gt 4$
has been studied in just a few works. Carocca, González-Aguilera, Hidalgo, and Rodríguez studied in [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
] the Humbert-Edge curves from the point of view of uniformization and Klenian groups. Using a suitable form of the quadrics, Hidalgo presented in [
Reference Gonzalez-Dorrego11
] and [
Reference Hidalgo12
] a family of Humbert-Edge curves of type 5 whose fields of moduli are contained in
![]() $\mathbb{R}$
but none of their fields of definition are contained in
$\mathbb{R}$
but none of their fields of definition are contained in
![]() $\mathbb{R}$
. Frías-Medina and Zamora presented in [
Reference Farkas and Kra9
] a characterization of Humbert-Edge curves using certain abelian groups of order
$\mathbb{R}$
. Frías-Medina and Zamora presented in [
Reference Farkas and Kra9
] a characterization of Humbert-Edge curves using certain abelian groups of order
![]() $2^n$
and presented specializations admitting larger automorphism subgroups. Carvacho, Hidalgo, and Quispe determined in [
Reference Carvacho, Hidalgo and Quispe4
] the decomposition of the Jacobian of generalized Fermat curves and as a consequence for Humbert-Edge curves. Auffarth, Lucchini Arteche, and Rojas described in [
Reference Auffarth, Lucchini Arteche and Rojas1
] the decomposition of the Jacobian of a Humbert-Edge curve more precisely given the exact number of factors in the decomposition and their corresponding dimensions.
$2^n$
and presented specializations admitting larger automorphism subgroups. Carvacho, Hidalgo, and Quispe determined in [
Reference Carvacho, Hidalgo and Quispe4
] the decomposition of the Jacobian of generalized Fermat curves and as a consequence for Humbert-Edge curves. Auffarth, Lucchini Arteche, and Rojas described in [
Reference Auffarth, Lucchini Arteche and Rojas1
] the decomposition of the Jacobian of a Humbert-Edge curve more precisely given the exact number of factors in the decomposition and their corresponding dimensions.
In the case
![]() $n=5$
, the normal form for these curves implies that they are contained in a special
$n=5$
, the normal form for these curves implies that they are contained in a special
![]() $K3$
surface, a Kummer surface. In this work, we study the Humbert-Edge curves of type 5 and determine some properties using the geometry of Kummer surfaces.
$K3$
surface, a Kummer surface. In this work, we study the Humbert-Edge curves of type 5 and determine some properties using the geometry of Kummer surfaces.
Recall that an algebraic (complex)
![]() $K3$
surface is a complete non-singular projective (compact connected complex) surface
$K3$
surface is a complete non-singular projective (compact connected complex) surface
![]() $S$
such that
$S$
such that
![]() $\omega _S\cong \mathcal{O}_S$
and
$\omega _S\cong \mathcal{O}_S$
and
![]() $H^1(S,\mathcal{O}_S)=0$
. Classically, a (singular) Kummer surface is a surface in
$H^1(S,\mathcal{O}_S)=0$
. Classically, a (singular) Kummer surface is a surface in
![]() ${\mathbb{P}}^3$
of degree 4 with 16 nodes and no other singularities. An important fact about Kummer surfaces is that are determined by the set of their nodes. One can take the resolution of singularities of a Kummer surface, and the obtained non-singular surface is a
${\mathbb{P}}^3$
of degree 4 with 16 nodes and no other singularities. An important fact about Kummer surfaces is that are determined by the set of their nodes. One can take the resolution of singularities of a Kummer surface, and the obtained non-singular surface is a
![]() $K3$
surface. For our purposes, these non-singular models will be called Kummer surfaces.
$K3$
surface. For our purposes, these non-singular models will be called Kummer surfaces.
The Kummer surfaces that we will take for our study are those coming from a hyperelliptic curve of genus 2. In such case, an important feature shared by Humbert-Edge curves of type 5 and Kummer surfaces is that they admit the automorphism subgroup generated by the natural involutions of
![]() ${\mathbb{P}}^5$
that change the
${\mathbb{P}}^5$
that change the
![]() $i$
th coordinate by its negative:
$i$
th coordinate by its negative:
These automorphisms along with Knutsen’s result [
Reference Hidalgo, Reyes-Carocca and Valdés14
] on the existence of a
![]() $K3$
surface of degree
$K3$
surface of degree
![]() $2n$
in
$2n$
in
![]() ${\mathbb{P}}^{n+1}$
containing a smooth curve of genus
${\mathbb{P}}^{n+1}$
containing a smooth curve of genus
![]() $g$
and degree
$g$
and degree
![]() $d$
will enable us to characterize the Humbert-Edge curves of type 5 using the geometry of a Kummer surface.
$d$
will enable us to characterize the Humbert-Edge curves of type 5 using the geometry of a Kummer surface.
This work is organized as follows. In Section 2, we review the construction of a Kummer surface from a two-dimensional torus and the conditions that ensure when a Kummer surface is projective. Later, we focus on the case of Kummer surfaces obtained from hyperelliptic curves of genus 2. Section 3 is split into three parts. First, in Section 3.1, we review the basic properties of Humbert-Edge curves of type 5 and characterize them using the geometry of the Kummer surface. Later, in Section 3.2, we present the construction of some odd theta characteristic on a Humbert-Edge curve of type 5 using the automorphisms
![]() $\sigma _i$
’s and some vanishing thetanulls using the Rosenhain tetrahedra associated with the Kummer surface. Finally, in Section 3.3 we use the embedding given in [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
] to construct an isomorphism between the moduli space
$\sigma _i$
’s and some vanishing thetanulls using the Rosenhain tetrahedra associated with the Kummer surface. Finally, in Section 3.3 we use the embedding given in [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
] to construct an isomorphism between the moduli space
![]() $\mathcal{HE}_5$
of Humbert-Edge curves of type 5 and the moduli space
$\mathcal{HE}_5$
of Humbert-Edge curves of type 5 and the moduli space
![]() $\mathcal{H}_2$
of hyperelliptic curves of genus 2, and as a consequence, we obtain that
$\mathcal{H}_2$
of hyperelliptic curves of genus 2, and as a consequence, we obtain that
![]() $\mathcal{H}_2$
is a three-dimensional closed subvariety of
$\mathcal{H}_2$
is a three-dimensional closed subvariety of
![]() $\mathcal{M}_{17}$
. Moreover, we generalized this argument to show that there is an isomorphism between the moduli space
$\mathcal{M}_{17}$
. Moreover, we generalized this argument to show that there is an isomorphism between the moduli space
![]() $\mathcal{HE}_n$
of Humbert-Edge curves of type
$\mathcal{HE}_n$
of Humbert-Edge curves of type
![]() $n$
, where
$n$
, where
![]() $n\geq 5$
is an odd number, and the moduli space
$n\geq 5$
is an odd number, and the moduli space
![]() $\mathcal{H}_{g}$
of hyperelliptic curves of genus
$\mathcal{H}_{g}$
of hyperelliptic curves of genus
![]() $g=\frac{n-1}{2}$
.
$g=\frac{n-1}{2}$
.
2. Kummer surfaces
2.1. Construction from a two-dimensional torus
In this paper, the ground field is the complex numbers. In this section, we recall the construction of the Kummer surface associated with a two-dimensional torus.
Let
![]() $T$
be a two-dimensional torus. Consider the involution
$T$
be a two-dimensional torus. Consider the involution
![]() $\iota \,:\,T\rightarrow T$
which sends
$\iota \,:\,T\rightarrow T$
which sends
![]() $a\mapsto -a$
and takes the quotient surface
$a\mapsto -a$
and takes the quotient surface
![]() $T/\langle \iota \rangle$
. The surface
$T/\langle \iota \rangle$
. The surface
![]() $T/\langle \iota \rangle$
is known as the singular Kummer surface of
$T/\langle \iota \rangle$
is known as the singular Kummer surface of
![]() $T$
. It is well-known that this surface has 16 ordinary singularities, and by resolving them, we obtain a
$T$
. It is well-known that this surface has 16 ordinary singularities, and by resolving them, we obtain a
![]() $K3$
surface called the Kummer surface of
$K3$
surface called the Kummer surface of
![]() $T$
and denoted by
$T$
and denoted by
![]() $\mathrm{Km}(T)$
(see e.g., [
Reference Frías-Medina and Zamora10
, Theorem 3.4]). This procedure is called the Kummer process. Note that by construction,
$\mathrm{Km}(T)$
(see e.g., [
Reference Frías-Medina and Zamora10
, Theorem 3.4]). This procedure is called the Kummer process. Note that by construction,
![]() $\mathrm{Km}(T)$
has 16 disjoint smooth rational curves; indeed, they correspond to the singular points of the quotient surface. Nikulin proved in [
Reference Knutsen15
] the converse:
$\mathrm{Km}(T)$
has 16 disjoint smooth rational curves; indeed, they correspond to the singular points of the quotient surface. Nikulin proved in [
Reference Knutsen15
] the converse:
Theorem 2.1.
If a
![]() $K3$
surface
$K3$
surface
![]() $S$
contains 16 disjoint smooth rational curves, then there exists a unique complex torus, up to isomorphism, such that
$S$
contains 16 disjoint smooth rational curves, then there exists a unique complex torus, up to isomorphism, such that
![]() $S$
and the rational curves are obtained by the Kummer process. In particular,
$S$
and the rational curves are obtained by the Kummer process. In particular,
![]() $S$
is a Kummer surface.
$S$
is a Kummer surface.
Note that the above construction holds true for any two-dimensional torus, not necessarily a projective one. In particular, with this process it is possible to construct
![]() $K3$
surfaces that are not projective. However, there is an equivalence between the projectivity of the torus and the associated
$K3$
surfaces that are not projective. However, there is an equivalence between the projectivity of the torus and the associated
![]() $K3$
surface (see [
Reference Birkenhake and Lange2
, Theorem 4.5.4]):
$K3$
surface (see [
Reference Birkenhake and Lange2
, Theorem 4.5.4]):
Theorem 2.2.
Let
![]() $T$
be a two-dimensional torus.
$T$
be a two-dimensional torus.
![]() $T$
is an abelian surface if and only if
$T$
is an abelian surface if and only if
![]() $\mathrm{Km}(T)$
is projective.
$\mathrm{Km}(T)$
is projective.
Now, if
![]() $A$
is a principally polarized abelian surface, then
$A$
is a principally polarized abelian surface, then
![]() $A$
is one of the following (see [
Reference Birkenhake and Lange2
, Corollary 11.8.2]):
$A$
is one of the following (see [
Reference Birkenhake and Lange2
, Corollary 11.8.2]):
-
(a) The Jacobian of a smooth hyperelliptic curve of genus 2 or
-
(b) The canonical polarized product of two elliptic curves.
As we will see next, Case (a) is the one of our interest.
2.2. Hyperelliptic curves of genus 2 and Kummer surfaces
We are interested in
![]() $K3$
surfaces that are a smooth complete intersection of type
$K3$
surfaces that are a smooth complete intersection of type
![]() $(2,2,2)$
in
$(2,2,2)$
in
![]() ${\mathbb{P}}^5$
, i.e. that are a complete intersection of three quadrics. Moreover, we restrict to the case in which the quadrics are diagonal. The interest of having diagonal quadrics defining the
${\mathbb{P}}^5$
, i.e. that are a complete intersection of three quadrics. Moreover, we restrict to the case in which the quadrics are diagonal. The interest of having diagonal quadrics defining the
![]() $K3$
surface is that they enable us to work with hyperelliptic curves of genus 2.
$K3$
surface is that they enable us to work with hyperelliptic curves of genus 2.
Indeed, let
![]() $C$
be the hyperelliptic curve of genus 2 given by the affine equation
$C$
be the hyperelliptic curve of genus 2 given by the affine equation
where
![]() $a_0,\dots,a_5\in \mathbb{C}$
and
$a_0,\dots,a_5\in \mathbb{C}$
and
![]() $a_i\neq a_j$
if
$a_i\neq a_j$
if
![]() $i\neq j$
. We can consider the jacobian surface
$i\neq j$
. We can consider the jacobian surface
![]() $J(C)$
associated with
$J(C)$
associated with
![]() $C$
, and applying the Kummer process, we obtain that the
$C$
, and applying the Kummer process, we obtain that the
![]() $K3$
surface
$K3$
surface
![]() $\mathrm{Km}(J(C))$
is isomorphic to the surface in
$\mathrm{Km}(J(C))$
is isomorphic to the surface in
![]() ${\mathbb{P}}^5$
defined by the complete intersection of the 3 diagonal quadrics by [
Reference Nikulin16
, Theorem 2.5]:
${\mathbb{P}}^5$
defined by the complete intersection of the 3 diagonal quadrics by [
Reference Nikulin16
, Theorem 2.5]:
 \begin{equation} Q_i=\sum _{j=0}^5 a_j^i x_j^2, \;i=0,1,2. \end{equation}
\begin{equation} Q_i=\sum _{j=0}^5 a_j^i x_j^2, \;i=0,1,2. \end{equation}
In order to obtain a hyperelliptic curve of genus 2 beginning with a smooth
![]() $K3$
surface
$K3$
surface
![]() $S$
in
$S$
in
![]() ${\mathbb{P}}^5$
given by the complete intersection of three diagonal quadrics, we may assume an additional hypothesis. Edge studied in [
Reference Edge6
] the Kummer surfaces defined by (2). One of his results establishes that whenever a surface
${\mathbb{P}}^5$
given by the complete intersection of three diagonal quadrics, we may assume an additional hypothesis. Edge studied in [
Reference Edge6
] the Kummer surfaces defined by (2). One of his results establishes that whenever a surface
![]() $X$
given by the intersection of three linearly independent quadrics has a common self-polar simplex
$X$
given by the intersection of three linearly independent quadrics has a common self-polar simplex
![]() $\Sigma$
in
$\Sigma$
in
![]() ${\mathbb{P}}^5$
and contains a line in general position, then the equations defining
${\mathbb{P}}^5$
and contains a line in general position, then the equations defining
![]() $X$
can be written with the form (2). Observe that this fact is equivalent to requiring that
$X$
can be written with the form (2). Observe that this fact is equivalent to requiring that
![]() $X$
contains 16 disjoint lines; indeed, using the natural involutions of
$X$
contains 16 disjoint lines; indeed, using the natural involutions of
![]() ${\mathbb{P}}^5$
one can obtain the other lines.
${\mathbb{P}}^5$
one can obtain the other lines.
Then, let
![]() $S$
be a smooth
$S$
be a smooth
![]() $K3$
surface in
$K3$
surface in
![]() ${\mathbb{P}}^5$
given by the complete intersection of the quadrics
${\mathbb{P}}^5$
given by the complete intersection of the quadrics
 \begin{equation*} Q_i=\sum _{j=0}^5 a_{ij} x_j^2, \;\;\; i=0, 1, 2, \end{equation*}
\begin{equation*} Q_i=\sum _{j=0}^5 a_{ij} x_j^2, \;\;\; i=0, 1, 2, \end{equation*}
where
![]() $a_{ij}\in \mathbb{C}$
for
$a_{ij}\in \mathbb{C}$
for
![]() $i=0,1,2$
and
$i=0,1,2$
and
![]() $j=0,\dots,5$
and assume that
$j=0,\dots,5$
and assume that
![]() $S$
contains 16 disjoint lines. As a consequence, we may assume that
$S$
contains 16 disjoint lines. As a consequence, we may assume that
![]() $S$
is given by the quadrics in (2) for some
$S$
is given by the quadrics in (2) for some
![]() $a_i\in \mathbb{C}$
where
$a_i\in \mathbb{C}$
where
![]() $a_i\neq a_j$
if
$a_i\neq a_j$
if
![]() $i\neq j$
. By [
Reference Knutsen15
, Theorem 1] there exists a unique (up to isomorphism) two-dimensional torus that gives rise to the surface
$i\neq j$
. By [
Reference Knutsen15
, Theorem 1] there exists a unique (up to isomorphism) two-dimensional torus that gives rise to the surface
![]() $S$
. Taking the hyperelliptic curve
$S$
. Taking the hyperelliptic curve
![]() $C$
given by the equation
$C$
given by the equation
![]() $y^2=f(x)=(x-a_0)(x-a_1)\cdots (x-a_5)$
, we obtain that
$y^2=f(x)=(x-a_0)(x-a_1)\cdots (x-a_5)$
, we obtain that
![]() $S$
is isomorphic to
$S$
is isomorphic to
![]() $\mathrm{Km}(J(C))$
.
$\mathrm{Km}(J(C))$
.
From now on, we say that a Kummer surface is a smooth surface in
![]() ${\mathbb{P}}^5$
given by the complete intersection of three diagonal quadrics as in (2).
${\mathbb{P}}^5$
given by the complete intersection of three diagonal quadrics as in (2).
For a Kummer surface
![]() $S$
given by (2), it is possible to give the parametric form of the 32 lines contained in
$S$
given by (2), it is possible to give the parametric form of the 32 lines contained in
![]() $S$
. Indeed, in [
Reference Edge6
] Edge noted that the equation of a line
$S$
. Indeed, in [
Reference Edge6
] Edge noted that the equation of a line
![]() $\ell$
contained in
$\ell$
contained in
![]() $S$
is given in the following parametric form:
$S$
is given in the following parametric form:
Recall that the natural automorphisms
![]() $\sigma _i\,:\, x_i\mapsto -x_i$
of
$\sigma _i\,:\, x_i\mapsto -x_i$
of
![]() ${\mathbb{P}}^5$
act on
${\mathbb{P}}^5$
act on
![]() $S$
. Denote by
$S$
. Denote by
![]() $E$
the group
$E$
the group
![]() $\langle \sigma _0,\dots,\sigma _5 \rangle$
. Applying each element of
$\langle \sigma _0,\dots,\sigma _5 \rangle$
. Applying each element of
![]() $E$
to the line
$E$
to the line
![]() $\ell$
, we obtain the other 32 lines on
$\ell$
, we obtain the other 32 lines on
![]() $S$
. The identity gives the line
$S$
. The identity gives the line
![]() $\ell$
and the remaining elements give the other 31 lines:
$\ell$
and the remaining elements give the other 31 lines:
 $\ell _i\,:\!=\,\sigma _i(\ell )$
for all
$\ell _i\,:\!=\,\sigma _i(\ell )$
for all
 $i\in \{0,\dots,5\}$
,
$i\in \{0,\dots,5\}$
, $\ell _{ij}\,:\!=\,\sigma _i\sigma _j(\ell )$
for different
$\ell _{ij}\,:\!=\,\sigma _i\sigma _j(\ell )$
for different
 $i,j\in \{0,\dots,5\}$
$i,j\in \{0,\dots,5\}$
 $\ell _{ijk}\,:\!=\,\sigma _i\sigma _j\sigma _k(\ell )$
for different
$\ell _{ijk}\,:\!=\,\sigma _i\sigma _j\sigma _k(\ell )$
for different
 $i,j,k\in \{0,\dots,5\}$
.
$i,j,k\in \{0,\dots,5\}$
.
It is well-known that a singular Kummer surface
![]() $K$
is birational to a Weddle surface
$K$
is birational to a Weddle surface
![]() $W$
(see e.g., [
Reference Shioda17
, Proposition 1]). A Weddle surface is a quartic surface in
$W$
(see e.g., [
Reference Shioda17
, Proposition 1]). A Weddle surface is a quartic surface in
![]() ${\mathbb{P}}^3$
with six nodes. The 32 lines on
${\mathbb{P}}^3$
with six nodes. The 32 lines on
![]() $S$
have a geometric interpretation in both
$S$
have a geometric interpretation in both
![]() $K$
and
$K$
and
![]() $W$
as Edge pointed in [
Reference Edge6
]. Indeed, the projection
$W$
as Edge pointed in [
Reference Edge6
]. Indeed, the projection
![]() $\pi$
of
$\pi$
of
![]() $S$
from
$S$
from
![]() $\ell$
is a Weddle surface
$\ell$
is a Weddle surface
![]() $W$
and it occurs:
$W$
and it occurs:
 $\pi (\ell _i)=k_i$
is a node on
$\pi (\ell _i)=k_i$
is a node on
 $W$
, for all
$W$
, for all
 $i=0,\dots,5$
,
$i=0,\dots,5$
, $\pi (\ell _{ij})$
is the line through
$\pi (\ell _{ij})$
is the line through
 $k_i$
and
$k_i$
and
 $k_j$
, for different indices
$k_j$
, for different indices
 $i,j\in \{0,\dots,5\}$
,
$i,j\in \{0,\dots,5\}$
, $\pi (\ell _{ijh})$
is the line in the intersection of the plane generated by
$\pi (\ell _{ijh})$
is the line in the intersection of the plane generated by
 $k_i,k_j,k_h$
with the complementary plane, for different indices
$k_i,k_j,k_h$
with the complementary plane, for different indices
 $i,j,h\in \{0,\dots,5\}$
, and
$i,j,h\in \{0,\dots,5\}$
, and $\pi (\ell )$
is the cubic on
$\pi (\ell )$
is the cubic on
 $W$
through the six nodes
$W$
through the six nodes
 $k_i$
’s.
$k_i$
’s.
On the other hand, since
![]() $S$
is the resolution of singularities of
$S$
is the resolution of singularities of
![]() $K$
it occurs:
$K$
it occurs:
The 16 nodes of
 $K$
correspond to the 16 lines
$K$
correspond to the 16 lines
 $\ell _{i}$
and
$\ell _{i}$
and
 $\ell _{ijk}$
, and
$\ell _{ijk}$
, andThe conics of contact of
 $K$
with its 16 tropes correspond to the 16 lines
$K$
with its 16 tropes correspond to the 16 lines
 $\ell$
and
$\ell$
and
 $\ell _{ij}$
.
$\ell _{ij}$
.
A trope is a plane which intersects the quartic along a conic. The nodes and the tropes of a singular Kummer surface provide an interesting configuration on it.
Definition 2.3.
Let
![]() $\Gamma$
be a set of
$\Gamma$
be a set of
![]() $16$
planes and
$16$
planes and
![]() $16$
points in
$16$
points in
![]() ${\mathbb{P}}^3$
.
${\mathbb{P}}^3$
.
 $\Gamma$
is a
$\Gamma$
is a
 $(16,6)$
-configuration if every plane contains exactly
$(16,6)$
-configuration if every plane contains exactly
 $6$
of the
$6$
of the
 $16$
points and every point lies in exactly
$16$
points and every point lies in exactly
 $6$
of the
$6$
of the
 $16$
planes. The 16 planes are called special planes.
$16$
planes. The 16 planes are called special planes.
A
 $(16,6)$
-configuration is non-degenerate if every two special planes share exactly two points of the configuration and every pair of points is contained in exactly two special planes.
$(16,6)$
-configuration is non-degenerate if every two special planes share exactly two points of the configuration and every pair of points is contained in exactly two special planes.
An abstract
 $(16,6)$
-configuration is a
$(16,6)$
-configuration is a
 $16\times 16$
matrix
$16\times 16$
matrix
 $(a_{ij})$
whose entries are ones or zeros, with exactly
$(a_{ij})$
whose entries are ones or zeros, with exactly
 $6$
ones in each row and in each column. The rows of the matrix are called points of the configuration, and the columns are called planes of the configuration. The
$6$
ones in each row and in each column. The rows of the matrix are called points of the configuration, and the columns are called planes of the configuration. The
 $i$
th point belongs to the
$i$
th point belongs to the
 $j$
th plane if and only if
$j$
th plane if and only if
 $a_{ij}=1$
.
$a_{ij}=1$
.
Gonzalez-Dorrego classified in [
Reference Frías-Medina and Zamora10
] the non-degenerate
![]() $(16,6)$
-configurations and used them to classify the singular Kummer surfaces. Given a singular Kummer surface, the nodes and the tropes establish a non-degenerate
$(16,6)$
-configurations and used them to classify the singular Kummer surfaces. Given a singular Kummer surface, the nodes and the tropes establish a non-degenerate
![]() $(16,6)$
-configuration (see [
Reference Frías-Medina and Zamora10
, Corollary 2.18]), and conversely, given a
$(16,6)$
-configuration (see [
Reference Frías-Medina and Zamora10
, Corollary 2.18]), and conversely, given a
![]() $(16,6)$
-configuration, there exists a singular Kummer surface whose associated
$(16,6)$
-configuration, there exists a singular Kummer surface whose associated
![]() $(16,6)$
-configuration is the given one (see [
Reference Frías-Medina and Zamora10
, Theorem 2.20]).
$(16,6)$
-configuration is the given one (see [
Reference Frías-Medina and Zamora10
, Theorem 2.20]).
Definition 2.4.
A Rosenhain tetrahedron in an abstract
![]() $(16,6)$
-configuration is a set of
$(16,6)$
-configuration is a set of
![]() $4$
points and
$4$
points and
![]() $4$
planes such that each plane contains exactly
$4$
planes such that each plane contains exactly
![]() $3$
points and each point belongs to exactly
$3$
points and each point belongs to exactly
![]() $3$
planes. The
$3$
planes. The
![]() $4$
points are the vertices of the tetrahedron. An edge is a pair of vertices, and a face is a triple of vertices.
$4$
points are the vertices of the tetrahedron. An edge is a pair of vertices, and a face is a triple of vertices.
Rosenhain tetrahedra always exist in a singular Kummer surface; in fact, there exist
![]() $80$
of them ([
Reference Frías-Medina and Zamora10
, Corollary 3.21]). Moreover, these tetrahedra are relevant because using them we can construct divisors that are linearly equivalent and whose class induces the closed embedding to
$80$
of them ([
Reference Frías-Medina and Zamora10
, Corollary 3.21]). Moreover, these tetrahedra are relevant because using them we can construct divisors that are linearly equivalent and whose class induces the closed embedding to
![]() ${\mathbb{P}}^5$
(see [
Reference Frías-Medina and Zamora10
, Proposition 3.22 and Remark 3.24]):
${\mathbb{P}}^5$
(see [
Reference Frías-Medina and Zamora10
, Proposition 3.22 and Remark 3.24]):
Proposition 2.5.
Given a Rosenhain tetrahedron on a singular Kummer surface
![]() $K$
, let
$K$
, let
![]() $D$
be the divisor on the associated Kummer surface
$D$
be the divisor on the associated Kummer surface
![]() $S$
given by the sum of proper transforms of the
$S$
given by the sum of proper transforms of the
![]() $4$
conics in which the planes meet on
$4$
conics in which the planes meet on
![]() $K$
and the
$K$
and the
![]() $4$
exceptional divisors corresponding to the
$4$
exceptional divisors corresponding to the
![]() $4$
nodes. Then, the linear equivalence class of
$4$
nodes. Then, the linear equivalence class of
![]() $D$
is independent of the choice of the Rosenhain tetrahedron. In addition,
$D$
is independent of the choice of the Rosenhain tetrahedron. In addition,
![]() $D^2=8$
,
$D^2=8$
,
![]() $\mathrm{dim}|D|=5$
, and the linear system
$\mathrm{dim}|D|=5$
, and the linear system
![]() $|D|$
induces a closed embedding of
$|D|$
induces a closed embedding of
![]() $S$
in
$S$
in
![]() ${\mathbb{P}}^5$
as the complete intersection of three quadrics.
${\mathbb{P}}^5$
as the complete intersection of three quadrics.
These divisors will be used in the next section to construct vanishing thetanulls on Humbert-Edge curves of type 5.
3. Humbert-Edge curves of type 5
3.1. Properties and characterization
Here, we review the main properties of the Humbert-Edge curves of type 5 and present a characterization using the lines lying on a Kummer surface.
Definition 3.1.
An irreducible, non-degenerate, and non-singular curve
![]() $X_5\subseteq{\mathbb{P}}^5$
is a Humbert-Edge curve of type 5 if it is the complete intersection of 4 diagonal quadrics
$X_5\subseteq{\mathbb{P}}^5$
is a Humbert-Edge curve of type 5 if it is the complete intersection of 4 diagonal quadrics
![]() $Q_0,\dots,Q_3$
:
$Q_0,\dots,Q_3$
:
 \begin{equation*} Q_i=\sum _{j=0}^5 a_{ij} x_j^2, \;\;\; i=0,\dots, 3. \end{equation*}
\begin{equation*} Q_i=\sum _{j=0}^5 a_{ij} x_j^2, \;\;\; i=0,\dots, 3. \end{equation*}
The basic properties of a Humbert-Edge curve of type 5 are stated below.
Lemma 3.2.
Let
![]() $X_5\subset{\mathbb{P}}^5$
be a Humbert-Edge curve of type 5. The following hold:
$X_5\subset{\mathbb{P}}^5$
be a Humbert-Edge curve of type 5. The following hold:
-
1.
 $X_5$
is a curve of degree 16.
$X_5$
is a curve of degree 16.
-
2. The genus of
 $X_5$
is equal to
$X_5$
is equal to
 $g(X_5)=17$
.
$g(X_5)=17$
. -
3. Every 4-minor of the matrix
 $(a_{ij})$
is non-degenerate.
$(a_{ij})$
is non-degenerate.
-
4.
 $X_5$
is non-trigonal.
$X_5$
is non-trigonal.
The diagonal form of the equations defining a Humbert-Edge curve
![]() $X_5$
of type 5 implies that it admits the action of the group
$X_5$
of type 5 implies that it admits the action of the group
![]() $E$
generated by the six involutions
$E$
generated by the six involutions
![]() $\sigma _i\,:\, x_i\mapsto -x_i$
acting with fixed points and whose product is the identity. Moreover, these involutions establish a relation between the Humbert-Edge curves of type 5 and the Humbert’s curves in
$\sigma _i\,:\, x_i\mapsto -x_i$
acting with fixed points and whose product is the identity. Moreover, these involutions establish a relation between the Humbert-Edge curves of type 5 and the Humbert’s curves in
![]() ${\mathbb{P}}^4$
. For every
${\mathbb{P}}^4$
. For every
![]() $i=0,\dots,5$
, we can consider the covering
$i=0,\dots,5$
, we can consider the covering
![]() $\pi _i\,:\,X_5\rightarrow X_5/\langle \sigma _i\rangle$
induced by the involution
$\pi _i\,:\,X_5\rightarrow X_5/\langle \sigma _i\rangle$
induced by the involution
![]() $\sigma _i$
. This is a two-to-one covering ramified at 16 points obtained as the intersection points of
$\sigma _i$
. This is a two-to-one covering ramified at 16 points obtained as the intersection points of
![]() $X_5$
with the hyperplane
$X_5$
with the hyperplane
![]() $V(x_i)$
. In addition, the quotient of
$V(x_i)$
. In addition, the quotient of
![]() $X_5/\langle \sigma _i\rangle$
is a Humbert’s curve in
$X_5/\langle \sigma _i\rangle$
is a Humbert’s curve in
![]() ${\mathbb{P}}^4$
. This double covering can be interpreted geometrically as the projection of
${\mathbb{P}}^4$
. This double covering can be interpreted geometrically as the projection of
![]() $X_5$
with center
$X_5$
with center
![]() $e_i$
onto the hyperplane
$e_i$
onto the hyperplane
![]() $V(x_i)$
.
$V(x_i)$
.
Next result shows that a Humbert-Edge curve of type 5 is always contained in a Kummer surface. It is a consequence of the fact noted by Edge in [
Reference Edge7
] that a Humbert-Edge curve of type
![]() $n$
can be written in a normal form.
$n$
can be written in a normal form.
Proposition 3.3.
Let
![]() $X_5\subset{\mathbb{P}}^5$
be a Humbert-Edge curve of type 5. There exists a Kummer surface in
$X_5\subset{\mathbb{P}}^5$
be a Humbert-Edge curve of type 5. There exists a Kummer surface in
![]() ${\mathbb{P}}^5$
which contains
${\mathbb{P}}^5$
which contains
![]() $X_5$
.
$X_5$
.
Proof. Assume that
![]() $X_5$
is given by the equations
$X_5$
is given by the equations
 \begin{equation*} Q_i=\sum _{j=0}^5 a_{ij} x_j^2, \;\;\; i=0,\dots,3 \end{equation*}
\begin{equation*} Q_i=\sum _{j=0}^5 a_{ij} x_j^2, \;\;\; i=0,\dots,3 \end{equation*}
where
![]() $a_{ij}\in \mathbb{C}$
. For each
$a_{ij}\in \mathbb{C}$
. For each
![]() $j=0,\dots,5$
, consider the coefficients
$j=0,\dots,5$
, consider the coefficients
![]() $a_{ij}$
as the entries of the point
$a_{ij}$
as the entries of the point
![]() $p_j=\left(a_{0j}\,:\,a_{1j}\,:\,a_{2j}\,:\,a_{3j}\right)$
in the projective space
$p_j=\left(a_{0j}\,:\,a_{1j}\,:\,a_{2j}\,:\,a_{3j}\right)$
in the projective space
![]() ${\mathbb{P}}^3$
. We have six points
${\mathbb{P}}^3$
. We have six points
![]() $p_0,\dots,p_5$
in
$p_0,\dots,p_5$
in
![]() ${\mathbb{P}}^3$
that are in general position, so there exists a unique rational normal curve
${\mathbb{P}}^3$
that are in general position, so there exists a unique rational normal curve
![]() $C\subset{\mathbb{P}}^3$
through these points. Finally, take a change of coordinates of
$C\subset{\mathbb{P}}^3$
through these points. Finally, take a change of coordinates of
![]() ${\mathbb{P}}^3$
such that
${\mathbb{P}}^3$
such that
![]() $C$
is in the standard parametric form, then we may assume that
$C$
is in the standard parametric form, then we may assume that
![]() $p_j=\left(1\,:\,a_j\,:\,a_j^2\,:\,a_j^3\right)$
for all
$p_j=\left(1\,:\,a_j\,:\,a_j^2\,:\,a_j^3\right)$
for all
![]() $j=0,\dots,5$
. Therefore, we obtain that
$j=0,\dots,5$
. Therefore, we obtain that
![]() $X_5$
is given by the equations
$X_5$
is given by the equations
 \begin{equation} Q_i=\sum _{j=0}^5 a_{j}^i x_j^2, \;\;\; i=0,\dots, 3 \end{equation}
\begin{equation} Q_i=\sum _{j=0}^5 a_{j}^i x_j^2, \;\;\; i=0,\dots, 3 \end{equation}
with
![]() $a_j\in \mathbb{C}, j=0,\dots,5$
and
$a_j\in \mathbb{C}, j=0,\dots,5$
and
![]() $a_j\neq a_k \mbox{ if } j\neq k$
. The quadrics
$a_j\neq a_k \mbox{ if } j\neq k$
. The quadrics
![]() $Q_0,Q_1,Q_2$
define the Kummer surface associated with the hyperelliptic curve
$Q_0,Q_1,Q_2$
define the Kummer surface associated with the hyperelliptic curve
![]() $y^2=\prod _{j=0}^5 (x-a_j)$
. Therefore,
$y^2=\prod _{j=0}^5 (x-a_j)$
. Therefore,
![]() $X_5$
is contained in a Kummer surface.
$X_5$
is contained in a Kummer surface.
Remark 3.4.
Note that given a Humbert-Edge curve
![]() $X_5$
of type 5 in normal form (4), by the above proposition it is always possible to find a hyperelliptic curve
$X_5$
of type 5 in normal form (4), by the above proposition it is always possible to find a hyperelliptic curve
![]() $C$
such that the Kummer surface
$C$
such that the Kummer surface
![]() $\mathrm{Km}(J(C))$
contains
$\mathrm{Km}(J(C))$
contains
![]() $X_5$
. Reciprocally, given a hyperelliptic curve
$X_5$
. Reciprocally, given a hyperelliptic curve
![]() $C$
of genus
$C$
of genus
![]() $2$
, by the discussion in Section 2.2, in a natural way the associated Kummer surface
$2$
, by the discussion in Section 2.2, in a natural way the associated Kummer surface
![]() $\mathrm{Km}(J(C))$
contains a Humbert-Edge curve of type 5 whose equations are in the normal form (4). Denote by
$\mathrm{Km}(J(C))$
contains a Humbert-Edge curve of type 5 whose equations are in the normal form (4). Denote by
![]() $\mathcal M_g$
the moduli space of smooth and irreducible curves of genus
$\mathcal M_g$
the moduli space of smooth and irreducible curves of genus
![]() $g$
. Note that Proposition 3.3 lets us see that Humbert-Edge curves of type 5 depend on three parameters in
$g$
. Note that Proposition 3.3 lets us see that Humbert-Edge curves of type 5 depend on three parameters in
![]() $\mathcal M_{17}$
; in fact in Section 3.3, we prove that the moduli space of Humbert-Edge curves of type 5 is isomorphic to the moduli space of hyperelliptic curves of genus 2.
$\mathcal M_{17}$
; in fact in Section 3.3, we prove that the moduli space of Humbert-Edge curves of type 5 is isomorphic to the moduli space of hyperelliptic curves of genus 2.
Next we present a characterization for Humbert-Edge curves of type 5 using the lines on Kummer surfaces.
Theorem 3.5.
Let
![]() $X\subset{\mathbb{P}}^5$
be an irreducible, non-degenerate, and non-singular curve of degree 16 and genus 17. The following statements are equivalent:
$X\subset{\mathbb{P}}^5$
be an irreducible, non-degenerate, and non-singular curve of degree 16 and genus 17. The following statements are equivalent:
-
(i)
 $X$
is a Humbert-Edge curve of type 5.
$X$
is a Humbert-Edge curve of type 5.
-
(ii)
 $X$
admits six involutions
$X$
admits six involutions
 $\sigma _0,\dots,\sigma _5$
such that
$\sigma _0,\dots,\sigma _5$
such that
 $\langle \sigma _0,\dots,\sigma _5\rangle \cong (\mathbb{Z}/2\mathbb{Z})^5$
,
$\langle \sigma _0,\dots,\sigma _5\rangle \cong (\mathbb{Z}/2\mathbb{Z})^5$
,
 $\sigma _0\cdots \sigma _5=1$
and the quotient
$\sigma _0\cdots \sigma _5=1$
and the quotient
 $X/\langle \sigma _i\rangle$
is a Humbert’s curve for every
$X/\langle \sigma _i\rangle$
is a Humbert’s curve for every
 $i=0,\dots,5$
.
$i=0,\dots,5$
. -
(iii) There exists a Kummer surface
 $S$
which contains
$S$
which contains
 $X$
and such that the intersection of
$X$
and such that the intersection of
 $X$
with the 16 lines
$X$
with the 16 lines
 $\ell$
and
$\ell$
and
 $\ell _{ij}$
is at most one point.
$\ell _{ij}$
is at most one point.
-
(iv) There exists a Kummer surface
 $S$
which contains
$S$
which contains
 $X$
and such that the intersection of
$X$
and such that the intersection of
 $X$
with the 16 lines
$X$
with the 16 lines
 $\ell _{i}$
and
$\ell _{i}$
and
 $\ell _{ijk}$
is at most one point.
$\ell _{ijk}$
is at most one point.
Proof. (i)
![]() $\Leftrightarrow$
(ii) We have this equivalence by [
Reference Farkas and Kra9
, Theorem 3.4].
$\Leftrightarrow$
(ii) We have this equivalence by [
Reference Farkas and Kra9
, Theorem 3.4].
(i)
![]() $\Rightarrow$
(iii) Assume that
$\Rightarrow$
(iii) Assume that
![]() $X$
is Humbert-Edge curve of type 5. Proposition 3.3 implies that
$X$
is Humbert-Edge curve of type 5. Proposition 3.3 implies that
![]() $X$
is contained in a Kummer surface
$X$
is contained in a Kummer surface
![]() $S$
. So, we may assume the existence of different scalars
$S$
. So, we may assume the existence of different scalars
![]() $a_0,\dots,a_5\in \mathbb{C}$
such that
$a_0,\dots,a_5\in \mathbb{C}$
such that
![]() $X$
is given by the equations
$X$
is given by the equations
 \begin{equation*} Q_i=\sum _{j=0}^5 a_{j}^i x_j^2, \;\;\;i=0,\dots,3 \end{equation*}
\begin{equation*} Q_i=\sum _{j=0}^5 a_{j}^i x_j^2, \;\;\;i=0,\dots,3 \end{equation*}
and
![]() $S$
is given by the equations
$S$
is given by the equations
![]() $Q_0,Q_1,Q_2$
. Consider the line
$Q_0,Q_1,Q_2$
. Consider the line
![]() $\ell$
in parametric form as in (3). A direct computation shows that for every
$\ell$
in parametric form as in (3). A direct computation shows that for every
![]() $t\in \mathbb{C}$
,
$t\in \mathbb{C}$
,
Therefore,
![]() $X$
does not intersect the line
$X$
does not intersect the line
![]() $\ell$
and the diagonal form of the third equation implies that
$\ell$
and the diagonal form of the third equation implies that
![]() $X$
also does not intersect the lines
$X$
also does not intersect the lines
![]() $\ell _{ij}$
for every
$\ell _{ij}$
for every
![]() $i,j\in \{0,\dots,5\}$
with
$i,j\in \{0,\dots,5\}$
with
![]() $i\neq j$
.
$i\neq j$
.
(iii)
![]() $\Rightarrow$
(i) Assume that
$\Rightarrow$
(i) Assume that
![]() $X$
is contained in a Kummer surface
$X$
is contained in a Kummer surface
![]() $S$
defined by the equations
$S$
defined by the equations
 \begin{equation*} Q_i= \sum _{j=0}^5 a_j^i x_j^2, \;\;\; i=0,1, 2, \end{equation*}
\begin{equation*} Q_i= \sum _{j=0}^5 a_j^i x_j^2, \;\;\; i=0,1, 2, \end{equation*}
where
![]() $a_j\neq a_k$
if
$a_j\neq a_k$
if
![]() $j\neq k$
, and such that
$j\neq k$
, and such that
![]() $X$
does not intersect the lines
$X$
does not intersect the lines
![]() $\ell$
,
$\ell$
,
![]() $\ell _{jk}$
in two different points for all
$\ell _{jk}$
in two different points for all
![]() $j,k\in \{0,\dots,5\}$
with
$j,k\in \{0,\dots,5\}$
with
![]() $j\neq k$
. We denote
$j\neq k$
. We denote
![]() $f(x)=\prod _{j=0}^5 (x-a_j)$
. Since
$f(x)=\prod _{j=0}^5 (x-a_j)$
. Since
![]() $S$
is a
$S$
is a
![]() $K3$
surface of type
$K3$
surface of type
![]() $(2,2,2)$
in
$(2,2,2)$
in
![]() ${\mathbb{P}}^5$
containing
${\mathbb{P}}^5$
containing
![]() $X$
, our situation should be one of the cases determined by Knutsen in [
Reference Hidalgo, Reyes-Carocca and Valdés14
, Theorem 6.1 (3)]. In fact, we are in Case a) of the latter, in Knutsen’s notation we have
$X$
, our situation should be one of the cases determined by Knutsen in [
Reference Hidalgo, Reyes-Carocca and Valdés14
, Theorem 6.1 (3)]. In fact, we are in Case a) of the latter, in Knutsen’s notation we have
![]() $n=4$
,
$n=4$
,
![]() $d=16$
,
$d=16$
,
![]() $g=17$
, and
$g=17$
, and
![]() $g=d^2/16 +1$
. Moreover, such a result implies that
$g=d^2/16 +1$
. Moreover, such a result implies that
![]() $X$
is the complete intersection of
$X$
is the complete intersection of
![]() $S$
and a hypersurface of degree
$S$
and a hypersurface of degree
![]() $d/8$
, i.e.
$d/8$
, i.e.
![]() $X$
is the complete intersection of four quadrics. Denote the fourth quadric by
$X$
is the complete intersection of four quadrics. Denote the fourth quadric by
 \begin{equation*} Q=\sum _{j=0}^5 d_j x_j^2 + \sum _{0\leq k \lt j\leq 5} d_{jk} x_jx_k. \end{equation*}
\begin{equation*} Q=\sum _{j=0}^5 d_j x_j^2 + \sum _{0\leq k \lt j\leq 5} d_{jk} x_jx_k. \end{equation*}
Now, when we evaluate the quadric
![]() $Q$
in the parametric form of
$Q$
in the parametric form of
![]() $\ell$
we obtain a quadratic equation with parameter
$\ell$
we obtain a quadratic equation with parameter
![]() $t$
with leading coefficient
$t$
with leading coefficient
 \begin{equation*} \frac {1}{\prod _{j=0}^5 f^{\prime}(a_j)} \left ( \sum _{j=0}^5 f^{\prime}(a_0)\cdots \widehat {f^{\prime}(a_j)} \cdots f^{\prime}(a_5) d_j + \sum _{0\leq k\lt j\leq 5} f^{\prime}(a_0)\cdots \sqrt {f^{\prime}(a_k)}\sqrt {f^{\prime}(a_j)} \cdots f^{\prime}(a_5) d_{jk} \right ). \end{equation*}
\begin{equation*} \frac {1}{\prod _{j=0}^5 f^{\prime}(a_j)} \left ( \sum _{j=0}^5 f^{\prime}(a_0)\cdots \widehat {f^{\prime}(a_j)} \cdots f^{\prime}(a_5) d_j + \sum _{0\leq k\lt j\leq 5} f^{\prime}(a_0)\cdots \sqrt {f^{\prime}(a_k)}\sqrt {f^{\prime}(a_j)} \cdots f^{\prime}(a_5) d_{jk} \right ). \end{equation*}
The hypothesis that
![]() $Q$
does not intersect the line
$Q$
does not intersect the line
![]() $\ell$
in two different points implies that such coefficient vanishes (the coefficient of
$\ell$
in two different points implies that such coefficient vanishes (the coefficient of
![]() $t$
could vanish but in such case the constant term must be different from zero). This also occurs for all of the 15 lines
$t$
could vanish but in such case the constant term must be different from zero). This also occurs for all of the 15 lines
![]() $\ell _{jk}$
by hypothesis, and then, we have 16 imposed conditions. The leading coefficient for the line
$\ell _{jk}$
by hypothesis, and then, we have 16 imposed conditions. The leading coefficient for the line
![]() $\ell _{jk}$
can be deduced from the above one, in fact, since the line
$\ell _{jk}$
can be deduced from the above one, in fact, since the line
![]() $\ell _{jk}$
is obtained from
$\ell _{jk}$
is obtained from
![]() $\ell$
by the application of
$\ell$
by the application of
![]() $\sigma _j\sigma _k$
, it is enough to add a negative sign to the coefficient of the terms
$\sigma _j\sigma _k$
, it is enough to add a negative sign to the coefficient of the terms
![]() $d_{rs}$
whenever
$d_{rs}$
whenever
![]() $r$
or
$r$
or
![]() $s$
are equal to
$s$
are equal to
![]() $j$
or
$j$
or
![]() $k$
. Solving the linear system in the variables
$k$
. Solving the linear system in the variables
![]() $d_j$
’s and
$d_j$
’s and
![]() $d_{jk}$
’s, we obtain that all the
$d_{jk}$
’s, we obtain that all the
![]() $d_{jk}$
’s are equal to zero, that
$d_{jk}$
’s are equal to zero, that
![]() $d_0,d_1,d_2,d_3$
, and
$d_0,d_1,d_2,d_3$
, and
![]() $d_4$
are free parameters and
$d_4$
are free parameters and
Therefore,
![]() $X$
is the complete intersection of four diagonal quadrics in
$X$
is the complete intersection of four diagonal quadrics in
![]() ${\mathbb{P}}^5$
and we conclude that it is a Humbert-Edge curve of type 5.
${\mathbb{P}}^5$
and we conclude that it is a Humbert-Edge curve of type 5.
(iii)
![]() $\Leftrightarrow$
(iv) As above, assuming that
$\Leftrightarrow$
(iv) As above, assuming that
![]() $X$
is contained in a Kummer surface
$X$
is contained in a Kummer surface
![]() $S$
defined by the equations
$S$
defined by the equations
 \begin{equation*} Q_i= \sum _{j=0}^5 a_j^i x_j^2, \;\;\; i=0, 1, 2, \end{equation*}
\begin{equation*} Q_i= \sum _{j=0}^5 a_j^i x_j^2, \;\;\; i=0, 1, 2, \end{equation*}
where
![]() $a_j\neq a_k$
if
$a_j\neq a_k$
if
![]() $j\neq k$
, by [
Reference Hidalgo, Reyes-Carocca and Valdés14
, Theorem 6.1 (3)] we ensure that
$j\neq k$
, by [
Reference Hidalgo, Reyes-Carocca and Valdés14
, Theorem 6.1 (3)] we ensure that
![]() $X$
is the complete intersection of
$X$
is the complete intersection of
![]() $S$
and a hypersurface of degree 2. Under the hypothesis of (iii) or (iv), when we solve the system of equations in the parameter
$S$
and a hypersurface of degree 2. Under the hypothesis of (iii) or (iv), when we solve the system of equations in the parameter
![]() $t$
as we previously did, we obtain that the coefficient of every mixed term vanishes and
$t$
as we previously did, we obtain that the coefficient of every mixed term vanishes and
![]() $d_5$
has the form of (5). The remaining conditions, (iv) or (iii), respectively, do not impose new conditions on the coefficients.
$d_5$
has the form of (5). The remaining conditions, (iv) or (iii), respectively, do not impose new conditions on the coefficients.
3.2. Theta characteristics
In this section, we use the coverings given by the subgroups generated by involutions
![]() $\sigma _i$
’s and the Rosenhain tetrahedra of singular Kummer surfaces to construct theta characteristics on a Humbert-Edge curve of type 5. We recall the definition of a theta characteristic and a vanishing thetanull.
$\sigma _i$
’s and the Rosenhain tetrahedra of singular Kummer surfaces to construct theta characteristics on a Humbert-Edge curve of type 5. We recall the definition of a theta characteristic and a vanishing thetanull.
Definition 3.6.
Let
![]() $X$
be an algebraic curve. A line bundle
$X$
be an algebraic curve. A line bundle
![]() $L$
on
$L$
on
![]() $X$
is a theta characteristic if
$X$
is a theta characteristic if
![]() $L^2\sim K_X$
. A theta characteristic
$L^2\sim K_X$
. A theta characteristic
![]() $L$
is even (respectively, odd) if
$L$
is even (respectively, odd) if
![]() $h^0(L)$
is even (respectively, odd). A vanishing thetanull is an even theta characteristic
$h^0(L)$
is even (respectively, odd). A vanishing thetanull is an even theta characteristic
![]() $L$
such that
$L$
such that
![]() $h^0(L)\gt 0$
.
$h^0(L)\gt 0$
.
Recall that given a Humbert-Edge curve
![]() $X_5$
of type 5, for every
$X_5$
of type 5, for every
![]() $i=0,\dots,5$
the double covering
$i=0,\dots,5$
the double covering
![]() $\pi _i\,:\,X_5\rightarrow X_5/\langle \sigma _i\rangle$
is ramified at 16 points obtained as the intersection points of
$\pi _i\,:\,X_5\rightarrow X_5/\langle \sigma _i\rangle$
is ramified at 16 points obtained as the intersection points of
![]() $X_5$
with the hyperplane
$X_5$
with the hyperplane
![]() $V(x_i)$
. Denote by
$V(x_i)$
. Denote by
![]() $R_i=p_{i1}+\cdots +p_{i16}$
the ramification divisor for every
$R_i=p_{i1}+\cdots +p_{i16}$
the ramification divisor for every
![]() $i=0,\dots,5$
.
$i=0,\dots,5$
.
Proposition 3.7.
Let
![]() $X_5\subset{\mathbb{P}}^5$
be a Humbert-Edge curve of type 5.
$X_5\subset{\mathbb{P}}^5$
be a Humbert-Edge curve of type 5.
![]() $X_5$
admits 26 odd theta characteristics with 3 sections, 6 of them correspond to the line bundle associated with the ramification divisors, and the remaining 20 are induced by the coverings associated with the subgroups generated by three different involutions
$X_5$
admits 26 odd theta characteristics with 3 sections, 6 of them correspond to the line bundle associated with the ramification divisors, and the remaining 20 are induced by the coverings associated with the subgroups generated by three different involutions
![]() $\sigma _i$
,
$\sigma _i$
,
![]() $\sigma _j$
and
$\sigma _j$
and
![]() $\sigma _k$
for
$\sigma _k$
for
![]() $i,j,k\in \{0,\dots,5\}$
.
$i,j,k\in \{0,\dots,5\}$
.
Proof. For distinct
![]() $i,j\in \{0,\dots,5\}$
, consider the subgroup generated by the involutions
$i,j\in \{0,\dots,5\}$
, consider the subgroup generated by the involutions
![]() $ \sigma _i$
and
$ \sigma _i$
and
![]() $\sigma _j$
and take the induced covering of degree four
$\sigma _j$
and take the induced covering of degree four
![]() $\pi _{ij}\,:\,X_5 \rightarrow X_5/\langle \sigma _i,\sigma _j\rangle$
. This is a simply ramified covering with the 32 ramified points
$\pi _{ij}\,:\,X_5 \rightarrow X_5/\langle \sigma _i,\sigma _j\rangle$
. This is a simply ramified covering with the 32 ramified points
![]() $p_{i1},\dots,p_{i16},p_{j1},\dots,p_{j16}$
. Since
$p_{i1},\dots,p_{i16},p_{j1},\dots,p_{j16}$
. Since
![]() $X_5/\langle \sigma _i,\sigma _j \rangle =E_{ij}$
is an elliptic curve, it follows that
$X_5/\langle \sigma _i,\sigma _j \rangle =E_{ij}$
is an elliptic curve, it follows that
So,
![]() $K_{X_5}\sim R_i+R_j$
for all
$K_{X_5}\sim R_i+R_j$
for all
![]() $i,j\in \{0,\dots,5\}$
. Fix and index
$i,j\in \{0,\dots,5\}$
. Fix and index
![]() $i\in \{0,\dots,5\}$
and take
$i\in \{0,\dots,5\}$
and take
![]() $j,k\in \{0,\dots,5\}\backslash \{i\}$
with
$j,k\in \{0,\dots,5\}\backslash \{i\}$
with
![]() $j\neq k$
. Using the fact that
$j\neq k$
. Using the fact that
we have that
![]() $R_i\sim R_j$
. Thus,
$R_i\sim R_j$
. Thus,
![]() $K_{X_5}\sim R_i+R_j\sim 2 R_i$
and
$K_{X_5}\sim R_i+R_j\sim 2 R_i$
and
![]() $R_i$
is a theta characteristic.
$R_i$
is a theta characteristic.
Now, let
![]() $i,j,k\in \{0,\dots,5\}$
be different indices. The covering of degree eight
$i,j,k\in \{0,\dots,5\}$
be different indices. The covering of degree eight
![]() $\pi _{ijk}\,:\,X_5\rightarrow X_5/\langle \sigma _i,\sigma _j,\sigma _k\rangle$
is a simply ramified covering in the 48 points
$\pi _{ijk}\,:\,X_5\rightarrow X_5/\langle \sigma _i,\sigma _j,\sigma _k\rangle$
is a simply ramified covering in the 48 points
![]() $p_{i1},\dots,p_{i16}, p_{j1},\dots,p_{j16}, p_{k1},\dots,p_{k16}$
. Note that
$p_{i1},\dots,p_{i16}, p_{j1},\dots,p_{j16}, p_{k1},\dots,p_{k16}$
. Note that
![]() $X_5/\langle \sigma _i,\sigma _j,\sigma _k\rangle \cong{\mathbb{P}}^1$
. Then,
$X_5/\langle \sigma _i,\sigma _j,\sigma _k\rangle \cong{\mathbb{P}}^1$
. Then,
Therefore, we have that
![]() $\pi _{ijk}^*(-K_{{\mathbb{P}}^1})\sim R_i$
and we conclude that
$\pi _{ijk}^*(-K_{{\mathbb{P}}^1})\sim R_i$
and we conclude that
![]() $\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2))$
is a theta characteristic of
$\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2))$
is a theta characteristic of
![]() $X_5$
.
$X_5$
.
Next step is to compute
![]() $h^0(\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2))$
. To do so, we will use the fact that
$h^0(\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2))$
. To do so, we will use the fact that
![]() $h^0(\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2)))=h^0({\pi _{ijk}}_*\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2)))$
. The covering
$h^0(\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2)))=h^0({\pi _{ijk}}_*\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2)))$
. The covering
![]() $\pi _{ijk}$
is determined by a line bundle
$\pi _{ijk}$
is determined by a line bundle
![]() $\mathcal{L}$
on
$\mathcal{L}$
on
![]() ${\mathbb{P}}^1$
such that
${\mathbb{P}}^1$
such that
![]() $\mathcal{L}^8=\mathcal{O}_{{\mathbb{P}}^1}({\pi _{ijk}}_*(Ri+R_j+R_k))$
, and in addition, we have that
$\mathcal{L}^8=\mathcal{O}_{{\mathbb{P}}^1}({\pi _{ijk}}_*(Ri+R_j+R_k))$
, and in addition, we have that
![]() ${\pi _{ijk}}_*\mathcal{O}_{X_5}=\mathcal{O}_{{\mathbb{P}}^1}\oplus \mathcal{L}^{-1}\oplus \cdots \oplus \mathcal{L}^{-7}$
. By the projection formula:
${\pi _{ijk}}_*\mathcal{O}_{X_5}=\mathcal{O}_{{\mathbb{P}}^1}\oplus \mathcal{L}^{-1}\oplus \cdots \oplus \mathcal{L}^{-7}$
. By the projection formula:
 \begin{align*}{\pi _{ijk}}_*\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2)) & = \mathcal{O}_{{\mathbb{P}}^1}(2) \otimes{\pi _{ijk}}_*\mathcal{O}_{X_5} \\ & = \mathcal{O}_{{\mathbb{P}}^1}(2) \otimes ( \mathcal{O}_{{\mathbb{P}}^1}\oplus \mathcal{L}^{-1}\oplus \cdots \oplus \mathcal{L}^{-7} ) \\ & = (\mathcal{O}_{{\mathbb{P}}^1}(2) \otimes \mathcal{O}_{{\mathbb{P}}^1}) \oplus (\mathcal{O}_{{\mathbb{P}}^1}(2) \otimes \mathcal{L}^{-1} ) \oplus \cdots \oplus (\mathcal{O}_{{\mathbb{P}}^1}(2) \otimes \mathcal{L}^{-7}). \end{align*}
\begin{align*}{\pi _{ijk}}_*\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2)) & = \mathcal{O}_{{\mathbb{P}}^1}(2) \otimes{\pi _{ijk}}_*\mathcal{O}_{X_5} \\ & = \mathcal{O}_{{\mathbb{P}}^1}(2) \otimes ( \mathcal{O}_{{\mathbb{P}}^1}\oplus \mathcal{L}^{-1}\oplus \cdots \oplus \mathcal{L}^{-7} ) \\ & = (\mathcal{O}_{{\mathbb{P}}^1}(2) \otimes \mathcal{O}_{{\mathbb{P}}^1}) \oplus (\mathcal{O}_{{\mathbb{P}}^1}(2) \otimes \mathcal{L}^{-1} ) \oplus \cdots \oplus (\mathcal{O}_{{\mathbb{P}}^1}(2) \otimes \mathcal{L}^{-7}). \end{align*}
From the equality
![]() $\mathcal{L}^8=\mathcal{O}_{{\mathbb{P}}^1}({\pi _{ijk}}_*(R_i+R_j+R_k))$
, we get that the degree of
$\mathcal{L}^8=\mathcal{O}_{{\mathbb{P}}^1}({\pi _{ijk}}_*(R_i+R_j+R_k))$
, we get that the degree of
![]() $\mathcal{L}$
is equal to 6, and this implies that
$\mathcal{L}$
is equal to 6, and this implies that
![]() $\mathcal{O}_{{\mathbb{P}}^1}(2) \otimes \mathcal{L}^{-n}$
has no sections for every
$\mathcal{O}_{{\mathbb{P}}^1}(2) \otimes \mathcal{L}^{-n}$
has no sections for every
![]() $n=1,\dots, 7$
. Therefore,
$n=1,\dots, 7$
. Therefore,
![]() ${\pi _{ijk}}_*\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2))=\mathcal{O}_{{\mathbb{P}}^1}(2)$
, and it follows that
${\pi _{ijk}}_*\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2))=\mathcal{O}_{{\mathbb{P}}^1}(2)$
, and it follows that
![]() $h^0(\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2)))=3$
. Finally, the line bundle
$h^0(\pi _{ijk}^*(\mathcal{O}_{{\mathbb{P}}^1}(2)))=3$
. Finally, the line bundle
![]() $\mathcal{O}_{X_5}(R_i)$
has 3 sections since
$\mathcal{O}_{X_5}(R_i)$
has 3 sections since
![]() $R_i\sim \pi _{ijk}^*(-K_{{\mathbb{P}}^1})$
.
$R_i\sim \pi _{ijk}^*(-K_{{\mathbb{P}}^1})$
.
Using the geometry of the Kummer surface, we can determine some vanishing thetanulls on a Humbert-Edge curve of type 5.
Proposition 3.8.
Let
![]() $X_5\subset{\mathbb{P}}^5$
be a Humbert-Edge curve of type 5.
$X_5\subset{\mathbb{P}}^5$
be a Humbert-Edge curve of type 5.
![]() $X_5$
admits 80 vanishing thetanulls with 6 sections corresponding to Rosenhain tetrahedra of the associated singular Kummer surface
$X_5$
admits 80 vanishing thetanulls with 6 sections corresponding to Rosenhain tetrahedra of the associated singular Kummer surface
![]() $K$
.
$K$
.
Proof. By Proposition 3.3,
![]() $X_5$
is contained in a Kummer surface
$X_5$
is contained in a Kummer surface
![]() $S$
. Denote by
$S$
. Denote by
![]() $K$
the singular Kummer surface associated with
$K$
the singular Kummer surface associated with
![]() $S$
. For a Rosenhain tetrahedron on
$S$
. For a Rosenhain tetrahedron on
![]() $K$
, let
$K$
, let
![]() $D$
be the associated divisor in
$D$
be the associated divisor in
![]() $S$
(see Proposition 2.5). By [
Reference Hidalgo, Reyes-Carocca and Valdés14
, Proposition 3.1], we have that
$S$
(see Proposition 2.5). By [
Reference Hidalgo, Reyes-Carocca and Valdés14
, Proposition 3.1], we have that
![]() $X_5$
and
$X_5$
and
![]() $D$
are dependent in
$D$
are dependent in
![]() $\mathrm{Pic}(S)$
; in fact,
$\mathrm{Pic}(S)$
; in fact,
![]() $X_5$
appears as an element in the linear system
$X_5$
appears as an element in the linear system
![]() $|2D|$
. Using the fact that the canonical bundle of
$|2D|$
. Using the fact that the canonical bundle of
![]() $S$
is trivial and that
$S$
is trivial and that
![]() $X_5\in |2D|$
, the adjunction formula implies that
$X_5\in |2D|$
, the adjunction formula implies that
Thus, the divisor
![]() $D|_{X_5}$
is a theta characteristic. Only the calculation of
$D|_{X_5}$
is a theta characteristic. Only the calculation of
![]() $h^0(D|_{X_5})$
remains. Twisting the exact sequence of sheaves
$h^0(D|_{X_5})$
remains. Twisting the exact sequence of sheaves
by
![]() $\mathcal{O}_S(D)$
, we obtain the exact sequence
$\mathcal{O}_S(D)$
, we obtain the exact sequence
and therefore, we obtain the exact sequence in cohomology
We have
![]() $H^0(S,-D)=0$
and since
$H^0(S,-D)=0$
and since
![]() $D$
is very ample, by Mumford vanishing theorem we obtain that
$D$
is very ample, by Mumford vanishing theorem we obtain that
![]() $H^1(S,-D)=0$
. Then,
$H^1(S,-D)=0$
. Then,
![]() $H^0(S, D) = H^0(X_5, D|_{X_5})$
and from
$H^0(S, D) = H^0(X_5, D|_{X_5})$
and from
![]() $\mathrm{dim}|D|=5$
it follows that
$\mathrm{dim}|D|=5$
it follows that
![]() $h^0(X_5, D|_{X_5})=6$
. We conclude the proof recalling that there are 80 Rosenhain tetrahedra associated with a singular Kummer surface (see Proposition 2.5).
$h^0(X_5, D|_{X_5})=6$
. We conclude the proof recalling that there are 80 Rosenhain tetrahedra associated with a singular Kummer surface (see Proposition 2.5).
We conclude this subsection with the following remarks:
The way to construct the vanishing thetanulls for a Humbert-Edge curve of type 5 using the geometry of a Kummer surface differs completely from the classical case: a Humbert’s curve
 $X$
admits exactly 10 vanishing thetanulls and can be constructed by taking the quotients of
$X$
admits exactly 10 vanishing thetanulls and can be constructed by taking the quotients of
 $X$
by the subgroup generated by two involutions (see the proof of [
Reference Farkas and Kra9
, Theorem 2.2]), the geometry of the Del Pezzo surface containing
$X$
by the subgroup generated by two involutions (see the proof of [
Reference Farkas and Kra9
, Theorem 2.2]), the geometry of the Del Pezzo surface containing
 $X$
is not involved in such process.
$X$
is not involved in such process.The procedure used in Proposition 3.8 to construct the vanishing thetanulls holds true for every smooth curve on degree 16 and genus 17 on a Kummer surface
 $S$
. Indeed, if
$S$
. Indeed, if
 $Y$
is any smooth curve of degree 16 and genus 17 contained in
$Y$
is any smooth curve of degree 16 and genus 17 contained in
 $S$
, then using again [
Reference Hidalgo, Reyes-Carocca and Valdés14
, Proposition 3.1] we have that
$S$
, then using again [
Reference Hidalgo, Reyes-Carocca and Valdés14
, Proposition 3.1] we have that
 $Y$
and
$Y$
and
 $D$
are dependent on
$D$
are dependent on
 $\mathrm{Pic}(S)$
and the previous argument holds.
$\mathrm{Pic}(S)$
and the previous argument holds.
3.3. Moduli space of Humbert-Edge curves of type 5
As we mention in Remark 3.4, given a Humbert-Edge curve of type 5 it is always possible to associate a hyperelliptic curve of genus 2 and vice versa. Here, we discuss about this fact, and using the results of Carocca, Gónzalez-Aguilera, Hidalgo, and Rodríguez [ Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3 ], we prove that the moduli space of Humbert-Edge curves of type 5 is isomorphic to the moduli space of hyperelliptic curves of genus 2.
Given a Humbert-Edge curve
![]() $X_5$
of type 5, using Edge’s idea of considering the coefficients as points in
$X_5$
of type 5, using Edge’s idea of considering the coefficients as points in
![]() ${\mathbb{P}}^3$
and the unique rational normal curve in
${\mathbb{P}}^3$
and the unique rational normal curve in
![]() ${\mathbb{P}}^3$
through them, one is able to write down the equations of
${\mathbb{P}}^3$
through them, one is able to write down the equations of
![]() $X_5$
in normal form (see the proof of Proposition 4):
$X_5$
in normal form (see the proof of Proposition 4):
 \begin{equation} Q_i=\sum _{j=0}^5 a_{j}^i x_j^2, \;\;\; i=0,\dots, 3, \end{equation}
\begin{equation} Q_i=\sum _{j=0}^5 a_{j}^i x_j^2, \;\;\; i=0,\dots, 3, \end{equation}
where
![]() $a_j\in \mathbb{C}$
for
$a_j\in \mathbb{C}$
for
![]() $j=0,\dots,5$
and
$j=0,\dots,5$
and
![]() $a_j\neq a_k$
if
$a_j\neq a_k$
if
![]() $j\neq k$
. Note that since the rational normal curve that we are considering is constructed via the Veronese map
$j\neq k$
. Note that since the rational normal curve that we are considering is constructed via the Veronese map
![]() $\nu \,:\,{\mathbb{P}}^1\rightarrow{\mathbb{P}}^3$
, one can fix three points in
$\nu \,:\,{\mathbb{P}}^1\rightarrow{\mathbb{P}}^3$
, one can fix three points in
![]() ${\mathbb{P}}^1$
, and therefore,
${\mathbb{P}}^1$
, and therefore,
![]() $X_5$
depends only on three different complex numbers. Thus, we can assume that we are fixing the points
$X_5$
depends only on three different complex numbers. Thus, we can assume that we are fixing the points
![]() $0,1$
, and
$0,1$
, and
![]() $\infty$
, and then, we have three free different parameters
$\infty$
, and then, we have three free different parameters
![]() $\lambda _1, \lambda _2$
, and
$\lambda _1, \lambda _2$
, and
![]() $\lambda _3$
defining the curve
$\lambda _3$
defining the curve
![]() $X_5$
. Since this idea can be carried out in the general case of Humbert-Edge curves of type
$X_5$
. Since this idea can be carried out in the general case of Humbert-Edge curves of type
![]() $n$
, with this fact in mind in [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
, Section 4.1] the authors found an embedding for Humbert-Edge curves of type
$n$
, with this fact in mind in [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
, Section 4.1] the authors found an embedding for Humbert-Edge curves of type
![]() $n$
in
$n$
in
![]() ${\mathbb{P}}^n$
in such way that the equations depend on
${\mathbb{P}}^n$
in such way that the equations depend on
![]() $n-2$
different parameters. In the particular case of the Humbert-Edge curve
$n-2$
different parameters. In the particular case of the Humbert-Edge curve
![]() $X_5$
of type 5, the equations take the form
$X_5$
of type 5, the equations take the form
 \begin{align*} x_0^2 + x_1^2+ x_2^2 & =0 \\ \lambda _1 x_0^2 + x_1^2 + x_3^2 & =0 \\ \lambda _2 x_0^2 + x_1^2+ x_4^2 & =0 \\ \lambda _3 x_0^2 + x_1^1 + x_5^2 &=0, \end{align*}
\begin{align*} x_0^2 + x_1^2+ x_2^2 & =0 \\ \lambda _1 x_0^2 + x_1^2 + x_3^2 & =0 \\ \lambda _2 x_0^2 + x_1^2+ x_4^2 & =0 \\ \lambda _3 x_0^2 + x_1^1 + x_5^2 &=0, \end{align*}
where
![]() $\lambda _1,\lambda _2,\lambda _3\in \mathbb{C}\backslash \{0,1\}$
are different complex numbers. To emphasize the dependence on the parameters
$\lambda _1,\lambda _2,\lambda _3\in \mathbb{C}\backslash \{0,1\}$
are different complex numbers. To emphasize the dependence on the parameters
![]() $\lambda _1,\lambda _2,\lambda _3$
and considering that we are fixing
$\lambda _1,\lambda _2,\lambda _3$
and considering that we are fixing
![]() $0,1,\infty$
, we denote this curve as
$0,1,\infty$
, we denote this curve as
![]() $X_5(\lambda _1,\lambda _2,\lambda _3)$
. Also, note that if we consider the degree 32 map given by
$X_5(\lambda _1,\lambda _2,\lambda _3)$
. Also, note that if we consider the degree 32 map given by
 \begin{align*} \pi _{(\lambda _1,\lambda _2,\lambda _3)}\,:\,X_5(\lambda _1,\lambda _2,\lambda _3) \rightarrow & \hspace{7mm}{\mathbb{P}}^1 \\ (x_0\,:\,\dots\, :\,x_5) \mapsto & -\left (\frac{x_1}{x_0}\right )^2, \end{align*}
\begin{align*} \pi _{(\lambda _1,\lambda _2,\lambda _3)}\,:\,X_5(\lambda _1,\lambda _2,\lambda _3) \rightarrow & \hspace{7mm}{\mathbb{P}}^1 \\ (x_0\,:\,\dots\, :\,x_5) \mapsto & -\left (\frac{x_1}{x_0}\right )^2, \end{align*}
then
is the branch locus of
![]() $\pi _{(\lambda _1,\lambda _2,\lambda _3)}$
.
$\pi _{(\lambda _1,\lambda _2,\lambda _3)}$
.
On the other hand, if
![]() $C$
is a hyperelliptic curve of genus 2, then we can write the equation which defines
$C$
is a hyperelliptic curve of genus 2, then we can write the equation which defines
![]() $C$
as
$C$
as
where
![]() $a_j\in \mathbb{C}$
for
$a_j\in \mathbb{C}$
for
![]() $j=0,\dots,5$
and
$j=0,\dots,5$
and
![]() $a_j\neq a_k$
if
$a_j\neq a_k$
if
![]() $j\neq k$
. Since there always exists an automorphism of
$j\neq k$
. Since there always exists an automorphism of
![]() ${\mathbb{P}}^1$
which carries a tuple of different complex numbers
${\mathbb{P}}^1$
which carries a tuple of different complex numbers
![]() $(a_0,a_1,a_2)$
to
$(a_0,a_1,a_2)$
to
![]() $(0,1,\infty )$
, we may assume that
$(0,1,\infty )$
, we may assume that
![]() $C$
is given by the equation
$C$
is given by the equation
where
![]() $\lambda _1,\lambda _2,\lambda _3\in \mathbb{C}\backslash \{0,1\}$
are different. Similarly as before, we denote by
$\lambda _1,\lambda _2,\lambda _3\in \mathbb{C}\backslash \{0,1\}$
are different. Similarly as before, we denote by
![]() $C(\lambda _1,\lambda _2,\lambda _3)$
the hyperelliptic curve of genus 2 with parameters
$C(\lambda _1,\lambda _2,\lambda _3)$
the hyperelliptic curve of genus 2 with parameters
![]() $0,1,\infty,\lambda _1,\lambda _2$
and
$0,1,\infty,\lambda _1,\lambda _2$
and
![]() $\lambda _3$
. In addition, since
$\lambda _3$
. In addition, since
![]() $C(\lambda _1,\lambda _2,\lambda _3)$
is a hyperelliptic curve of genus 2, there exists a degree 2 map
$C(\lambda _1,\lambda _2,\lambda _3)$
is a hyperelliptic curve of genus 2, there exists a degree 2 map
![]() $\rho _{(\lambda _1,\lambda _2,\lambda _3)}\,:\,C(\lambda _1,\lambda _2,\lambda _3)\rightarrow{\mathbb{P}}^1$
whose branch locus is precisely given by (7).
$\rho _{(\lambda _1,\lambda _2,\lambda _3)}\,:\,C(\lambda _1,\lambda _2,\lambda _3)\rightarrow{\mathbb{P}}^1$
whose branch locus is precisely given by (7).
In both cases of Humbert-Edge curves of type 5 and hyperelliptic curves of genus 2, given such a curve we have a map to
![]() ${\mathbb{P}}^1$
with a specific branch locus. In fact, the branch locus determines the curve modulo isomorphism. Indeed, Hidalgo, Reyes-Carocca, and Valdés determined in [
Reference Hidalgo13
, Section 2.3] when two generalized Fermat curves are isomorphic, in particular, the following result can be deduced:
${\mathbb{P}}^1$
with a specific branch locus. In fact, the branch locus determines the curve modulo isomorphism. Indeed, Hidalgo, Reyes-Carocca, and Valdés determined in [
Reference Hidalgo13
, Section 2.3] when two generalized Fermat curves are isomorphic, in particular, the following result can be deduced:
Proposition 3.9.
Let
![]() $X_5(\lambda _1,\lambda _2,\lambda _3)$
and
$X_5(\lambda _1,\lambda _2,\lambda _3)$
and
![]() $X_5(\mu _1,\mu _2,\mu _3)$
be Humbert-Edge curves of type 5. The following statements are equivalent:
$X_5(\mu _1,\mu _2,\mu _3)$
be Humbert-Edge curves of type 5. The following statements are equivalent:
-
1.
 $X_5(\lambda _1,\lambda _2,\lambda _3)$
is isomorphic to
$X_5(\lambda _1,\lambda _2,\lambda _3)$
is isomorphic to
 $X_5(\mu _1,\mu _2,\mu _3)$
.
$X_5(\mu _1,\mu _2,\mu _3)$
. -
2. There exists a Möbius transformation
 $M$
such that
$M$
such that
 \begin{equation*} \{M(0),M(1),M(\infty ),M(\lambda _1),M(\lambda _2),M(\lambda _3)\}=\{0,1,\infty,\mu _1,\mu _2,\mu _3\}. \end{equation*}
\begin{equation*} \{M(0),M(1),M(\infty ),M(\lambda _1),M(\lambda _2),M(\lambda _3)\}=\{0,1,\infty,\mu _1,\mu _2,\mu _3\}. \end{equation*}
In the case of hyperelliptic curves of genus 2, we have an analogous result (see [ Reference Edge8 , Section III.7.3]):
Proposition 3.10.
Let
![]() $C(\lambda _1,\lambda _2,\lambda _3)$
and
$C(\lambda _1,\lambda _2,\lambda _3)$
and
![]() $C(\mu _1,\mu _2,\mu _3)$
be hyperelliptic curves of genus 2. The following statements are equivalent:
$C(\mu _1,\mu _2,\mu _3)$
be hyperelliptic curves of genus 2. The following statements are equivalent:
-
1.
 $C(\lambda _1,\lambda _2,\lambda _3)$
is isomorphic to
$C(\lambda _1,\lambda _2,\lambda _3)$
is isomorphic to
 $C(\mu _1,\mu _2,\mu _3)$
.
$C(\mu _1,\mu _2,\mu _3)$
. -
2. There exists a Möbius transformation
 $M$
such that
$M$
such that
 \begin{equation*} \{M(0),M(1),M(\infty ),M(\lambda _1),M(\lambda _2),M(\lambda _3)\}=\{0,1,\infty,\mu _1,\mu _2,\mu _3\}. \end{equation*}
\begin{equation*} \{M(0),M(1),M(\infty ),M(\lambda _1),M(\lambda _2),M(\lambda _3)\}=\{0,1,\infty,\mu _1,\mu _2,\mu _3\}. \end{equation*}
The above results can be summarized in the following commuting diagram:

Now, we briefly discuss the construction of the moduli space of Humbert-Edge curves of type
![]() $5$
. To construct such moduli space, we follow Section 4.2 of [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
]. Let
$5$
. To construct such moduli space, we follow Section 4.2 of [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
]. Let
![]() $HE_5$
be the set of all Humbert-Edge curves of type 5. Since any Humbert-Edge curve of type 5 has genus 17, we have a map
$HE_5$
be the set of all Humbert-Edge curves of type 5. Since any Humbert-Edge curve of type 5 has genus 17, we have a map
![]() $r_5\,:\, HE_5\to\mathcal{M}_{17}$
defined by
$r_5\,:\, HE_5\to\mathcal{M}_{17}$
defined by
![]() $r_5(X_5(\lambda_1,\lambda_2,\lambda_3))=[X_5(\lambda_1,\lambda_2,\lambda_3)]$
, where
$r_5(X_5(\lambda_1,\lambda_2,\lambda_3))=[X_5(\lambda_1,\lambda_2,\lambda_3)]$
, where
![]() $\mathcal{M}_{17}$
is the moduli space of curves of genus 17. By Proposition 3.9, we can consider the isomorphism class of a Humbert-Edge curve of type 5, and this gives an equivalence relation on
$\mathcal{M}_{17}$
is the moduli space of curves of genus 17. By Proposition 3.9, we can consider the isomorphism class of a Humbert-Edge curve of type 5, and this gives an equivalence relation on
![]() $HE_5$
. Let
$HE_5$
. Let
![]() $\mathcal{HE}_5$
be the set obtained from this equivalence relation. We have a projection map
$\mathcal{HE}_5$
be the set obtained from this equivalence relation. We have a projection map
![]() $p_5\,:\,HE_5 \to\mathcal{HE}_5$
, and we have a well-defined map
$p_5\,:\,HE_5 \to\mathcal{HE}_5$
, and we have a well-defined map
![]() $q_5\,:\,\mathcal{HE}_5\to\mathcal{M}_{17}$
so that
$q_5\,:\,\mathcal{HE}_5\to\mathcal{M}_{17}$
so that
![]() $r_5=q_5\circ p_5$
. We have that
$r_5=q_5\circ p_5$
. We have that
![]() $\mathcal{HE}_5$
is a moduli space, and we call it the moduli space of Humbert-Edge curves of type 5, that is the set of Humbert-Edge curves of type 5 modulo isomorphism.
$\mathcal{HE}_5$
is a moduli space, and we call it the moduli space of Humbert-Edge curves of type 5, that is the set of Humbert-Edge curves of type 5 modulo isomorphism.
We denote by
![]() $\mathcal{H}_2$
the moduli space of hyperelliptic curves of genus 2. By Propositions 3.10 and 3.9, we have a well-defined map
$\mathcal{H}_2$
the moduli space of hyperelliptic curves of genus 2. By Propositions 3.10 and 3.9, we have a well-defined map
By construction, it is immediate that
![]() $f_5$
is a surjective map. The following proposition deals with the injectivity.
$f_5$
is a surjective map. The following proposition deals with the injectivity.
Proposition 3.11.
The above map
![]() $f_5\,:\,\mathcal{H}_2 \rightarrow \mathcal{HE}_5$
is injective. Therefore,
$f_5\,:\,\mathcal{H}_2 \rightarrow \mathcal{HE}_5$
is injective. Therefore,
![]() $f_5$
is an isomorphism of moduli spaces.
$f_5$
is an isomorphism of moduli spaces.
Proof. Let
![]() $C(\lambda _1,\lambda _2,\lambda _3)$
and
$C(\lambda _1,\lambda _2,\lambda _3)$
and
![]() $C(\mu _1,\mu _2,\mu _3)$
be hyperelliptic curves of genus 2. Assume that
$C(\mu _1,\mu _2,\mu _3)$
be hyperelliptic curves of genus 2. Assume that
![]() $f_5([C(\lambda _1,\lambda _2,\lambda _3)])=f_5([C(\mu _1,\mu _2,\mu _3)])$
; that is
$f_5([C(\lambda _1,\lambda _2,\lambda _3)])=f_5([C(\mu _1,\mu _2,\mu _3)])$
; that is
![]() $[X_5(\lambda _1,\lambda _2,\lambda _3)]=[X_5(\mu _1,\mu _2,\mu _3)]$
. Then, there exists an isomorphism between
$[X_5(\lambda _1,\lambda _2,\lambda _3)]=[X_5(\mu _1,\mu _2,\mu _3)]$
. Then, there exists an isomorphism between
![]() $X_5(\lambda _1,\lambda _2,\lambda _3)$
and
$X_5(\lambda _1,\lambda _2,\lambda _3)$
and
![]() $X_5(\mu _1,\mu _2,\mu _3)$
. By Proposition 3.9, there exists a Möbius transformation
$X_5(\mu _1,\mu _2,\mu _3)$
. By Proposition 3.9, there exists a Möbius transformation
![]() $M$
such that
$M$
such that
Thus, by Proposition 3.10 we conclude that the hyperelliptic curves
![]() $C(\lambda _1,\lambda _2,\lambda _3)$
and
$C(\lambda _1,\lambda _2,\lambda _3)$
and
![]() $C(\mu _1,\mu _2,\mu _3)$
are isomorphic.
$C(\mu _1,\mu _2,\mu _3)$
are isomorphic.
On the other hand, in [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
, Proposition 4.3] the authors proved that the map
![]() $q_5\,:\,\mathcal{HE}_5\to \mathcal{M}_{17}$
is injective. Thus, using the isomorphism
$q_5\,:\,\mathcal{HE}_5\to \mathcal{M}_{17}$
is injective. Thus, using the isomorphism
![]() $f_5$
we obtain the following:
$f_5$
we obtain the following:
Corollary 3.12.
The moduli space
![]() $\mathcal{H}_2$
of hyperelliptic curves of genus 2 is a three-dimensional closed algebraic variety in
$\mathcal{H}_2$
of hyperelliptic curves of genus 2 is a three-dimensional closed algebraic variety in
![]() $\mathcal{M}_{17}$
via the composition
$\mathcal{M}_{17}$
via the composition
![]() $q_5\circ f_5\,:\, \mathcal{H}_2 \hookrightarrow \mathcal{M}_{17}$
.
$q_5\circ f_5\,:\, \mathcal{H}_2 \hookrightarrow \mathcal{M}_{17}$
.
We conclude this paper noting that in the general case, the moduli space of Humbert-Edge curves of type
![]() $n$
, where
$n$
, where
![]() $n\geq 5$
is an odd number, is isomorphic to the moduli space of hyperelliptic curves of genus
$n\geq 5$
is an odd number, is isomorphic to the moduli space of hyperelliptic curves of genus
![]() $\frac{n-1}{2}$
. In general, a Humbert-Edge curve
$\frac{n-1}{2}$
. In general, a Humbert-Edge curve
![]() $X_n(\lambda _1,\dots,\lambda _{n-2})$
of type
$X_n(\lambda _1,\dots,\lambda _{n-2})$
of type
![]() $n$
in
$n$
in
![]() ${\mathbb{P}}^n$
can be written as
${\mathbb{P}}^n$
can be written as
 \begin{align*} x_0^2 + x_1^2+ x_2^2 & =0 \\ \lambda _1 x_0^2 + x_1^2 + x_3^2 & =0 \\ \lambda _2 x_0^2 + x_1^2+ x_4^2 & =0 \\ & \vdots \\ \lambda _{n-2} x_0^2 + x_1^1 + x_n^2 &=0, \end{align*}
\begin{align*} x_0^2 + x_1^2+ x_2^2 & =0 \\ \lambda _1 x_0^2 + x_1^2 + x_3^2 & =0 \\ \lambda _2 x_0^2 + x_1^2+ x_4^2 & =0 \\ & \vdots \\ \lambda _{n-2} x_0^2 + x_1^1 + x_n^2 &=0, \end{align*}
where
![]() $\lambda _1,\dots,\lambda _{n-2}\in \mathbb{C}\backslash \{0,1\}$
are different (see [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
, Section 4.1]).
$\lambda _1,\dots,\lambda _{n-2}\in \mathbb{C}\backslash \{0,1\}$
are different (see [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
, Section 4.1]).
Since we have an analogous of Proposition 3.9 for the general case (see [
Reference Hidalgo13
, Section 2.3]), then the argument to construct the moduli space of Humbert-Edge curves of type
![]() $5$
in fact holds true for the general case of Humbert-Edge curves of type
$5$
in fact holds true for the general case of Humbert-Edge curves of type
![]() $n$
(see Section 4.2 of [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
]). Therefore, we can consider the moduli space
$n$
(see Section 4.2 of [
Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3
]). Therefore, we can consider the moduli space
![]() $\mathcal{HE}_n$
of Humbert-Edge curves of type
$\mathcal{HE}_n$
of Humbert-Edge curves of type
![]() $n$
, and we have a well-defined map
$n$
, and we have a well-defined map
![]() $q_n\,:\,\mathcal{HE}_n\to \mathcal{M}_{g_n}$
where
$q_n\,:\,\mathcal{HE}_n\to \mathcal{M}_{g_n}$
where
![]() $\mathcal{M}_{g_n}$
is the moduli space of curves of genus
$\mathcal{M}_{g_n}$
is the moduli space of curves of genus
![]() $g_n=2^{n-2}(n-3)+1$
.
$g_n=2^{n-2}(n-3)+1$
.
On the other hand, a hyperelliptic curve
![]() $C(\lambda _1,\dots,\lambda _{2g-1})$
of genus
$C(\lambda _1,\dots,\lambda _{2g-1})$
of genus
![]() $g$
is given by the equation
$g$
is given by the equation
where
![]() $\lambda _1,\dots,\lambda _{2g-1}\in \mathbb{C}\backslash \{0,1\}$
are different. Since also Proposition 3.10 can be generalized in this general context (see [
Reference Edge8
, Section III.7.3]), under the assumptions that
$\lambda _1,\dots,\lambda _{2g-1}\in \mathbb{C}\backslash \{0,1\}$
are different. Since also Proposition 3.10 can be generalized in this general context (see [
Reference Edge8
, Section III.7.3]), under the assumptions that
![]() $n\geq 5$
is odd and
$n\geq 5$
is odd and
![]() $n-2=2g-1=d$
, we can define a surjective map
$n-2=2g-1=d$
, we can define a surjective map
where
![]() $\mathcal{H}_g$
denotes the moduli space of hyperelliptic curves of genus
$\mathcal{H}_g$
denotes the moduli space of hyperelliptic curves of genus
![]() $g=\frac{n-1}{2}$
. Finally, applying the argument of Proposition 3.11 and using the fact that the natural map
$g=\frac{n-1}{2}$
. Finally, applying the argument of Proposition 3.11 and using the fact that the natural map
![]() $q_n\,:\,\mathcal{HE}_n\rightarrow \mathcal{M}_{g_n}$
is injective (see [Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3, Proposition 4.3]) we conclude the following:
$q_n\,:\,\mathcal{HE}_n\rightarrow \mathcal{M}_{g_n}$
is injective (see [Reference Carocca, González-Aguilera, Hidalgo and Rodríguez3, Proposition 4.3]) we conclude the following:
Proposition 3.13.
If
![]() $n\geq 5$
is an odd number and
$n\geq 5$
is an odd number and
![]() $n-2=2g-1=d$
, then the map
$n-2=2g-1=d$
, then the map
![]() $f_d\,:\,\mathcal{H}_g \rightarrow \mathcal{HE}_n$
is an isomorphism of moduli spaces. In particular, we have that
$f_d\,:\,\mathcal{H}_g \rightarrow \mathcal{HE}_n$
is an isomorphism of moduli spaces. In particular, we have that
![]() $\mathcal{H}_g$
is an
$\mathcal{H}_g$
is an
![]() $(n-2)$
-dimensional closed variety in
$(n-2)$
-dimensional closed variety in
![]() $\mathcal{M}_{g_n}$
via the composition
$\mathcal{M}_{g_n}$
via the composition
![]() $q_n\circ f_d\,:\,\mathcal{H}_g\hookrightarrow \mathcal{M}_{g_n}$
, where
$q_n\circ f_d\,:\,\mathcal{H}_g\hookrightarrow \mathcal{M}_{g_n}$
, where
![]() $g_n=2^{n-2}(n-3)+1$
.
$g_n=2^{n-2}(n-3)+1$
.
Acknowledgements
The first author is supported by Grants PAPIIT UNAM IN100419 “Aspectos Geométricos del moduli de curvas
![]() $M_g$
” and CONACyT, México A1-S-9029 “Moduli de curvas y curvatura en
$M_g$
” and CONACyT, México A1-S-9029 “Moduli de curvas y curvatura en
![]() $A_g$
.” The second author was supported by Programa de Becas Posdoctorales 2019, DGAPA, UNAM. The second author was additionally supported by “Programa de Estancias Posdoctorales por México Convocatoria 2021 y 2022” from CONACYT during revisions of this article. The authors acknowledge the support of UNAM for the OA publication.
$A_g$
.” The second author was supported by Programa de Becas Posdoctorales 2019, DGAPA, UNAM. The second author was additionally supported by “Programa de Estancias Posdoctorales por México Convocatoria 2021 y 2022” from CONACYT during revisions of this article. The authors acknowledge the support of UNAM for the OA publication.