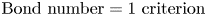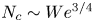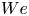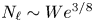Refine search
Actions for selected content:
13 results
EFFECT OF EXTERNAL HARMONIC VIBRATION ON THE FORMATION OF SOLITARY WAVES IN FALLING TWO-LAYER LIQUID FILMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 16 October 2024, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-Galilean Taylor–Culick law governs sheet dynamics in unsteady fragmentation
-
- Journal:
- Journal of Fluid Mechanics / Volume 969 / 25 August 2023
- Published online by Cambridge University Press:
- 15 August 2023, A19
-
- Article
- Export citation
FULLY 3D FLUID OUTFLOW FROM A SPHERICAL SOURCE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 10 August 2022, pp. 149-182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Growth and breakup of ligaments in unsteady fragmentation
-
- Journal:
- Journal of Fluid Mechanics / Volume 910 / 10 March 2021
- Published online by Cambridge University Press:
- 18 January 2021, A39
-
- Article
- Export citation
Fluid deformable surfaces
-
- Journal:
- Journal of Fluid Mechanics / Volume 878 / 10 November 2019
- Published online by Cambridge University Press:
- 04 September 2019, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Analytical formulae for longitudinal slip lengths over unidirectional superhydrophobic surfaces with curved menisci
-
- Journal:
- Journal of Fluid Mechanics / Volume 791 / 25 March 2016
- Published online by Cambridge University Press:
- 24 February 2016, R7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Drag and diffusion coefficients of a spherical particle attached to a fluid–fluid interface
-
- Journal:
- Journal of Fluid Mechanics / Volume 790 / 10 March 2016
- Published online by Cambridge University Press:
- 10 February 2016, pp. 607-618
-
- Article
- Export citation
Regimes during liquid drop impact on a liquid pool
-
- Journal:
- Journal of Fluid Mechanics / Volume 768 / 10 April 2015
- Published online by Cambridge University Press:
- 10 March 2015, pp. 492-523
-
- Article
- Export citation
Impact of liquids with different densities
-
- Journal:
- Journal of Fluid Mechanics / Volume 766 / 10 March 2015
- Published online by Cambridge University Press:
- 30 January 2015, pp. 5-27
-
- Article
- Export citation
Bridging local to global dynamics of drop impact onto solid substrates
-
- Journal:
- Journal of Fluid Mechanics / Volume 747 / 25 May 2014
- Published online by Cambridge University Press:
- 14 April 2014, pp. 103-118
-
- Article
- Export citation
Hydrothermal waves on ethanol droplets evaporating under terrestrial and reduced gravity levels
-
- Journal:
- Journal of Fluid Mechanics / Volume 712 / 10 December 2012
- Published online by Cambridge University Press:
- 05 November 2012, pp. 614-623
-
- Article
- Export citation
Occlusion criteria in tubes under transverse body forces
-
- Journal:
- Journal of Fluid Mechanics / Volume 682 / 10 September 2011
- Published online by Cambridge University Press:
- 13 July 2011, pp. 397-414
-
- Article
- Export citation
Instabilities in free-surface Hartmann flow at low magnetic Prandtl numbers
-
- Journal:
- Journal of Fluid Mechanics / Volume 636 / 10 October 2009
- Published online by Cambridge University Press:
- 25 September 2009, pp. 217-277
-
- Article
- Export citation