1 Introduction
Faraday waves are standing surface waves that develop at the interface between two immiscible fluids or between a fluid and a gas, when subjected to a harmonic vibration usually induced perpendicularly to the interface [Reference Faraday4]. Since the discovery of these waves in 1831, an enormous amount of theoretical and experimental studies have been conducted to investigate properties of linear and nonlinear Faraday waves in one- and multilayer liquid films. One of many intriguing questions that has received much attention is whether Faraday instability can be used to alter (suppress or enhance) other types of instabilities such as Rayleigh–Taylor or long-wave gravity driven instabilities that develop in liquid layers flowing down an incline.
The linear stability of a flat liquid layer on a vibrated incline was studied by Woods and Lin [Reference Woods and Lin23]. By linearizing Navier–Stokes equations about a steady flow down an incline, a general mathematical analysis based on Floquet theory [Reference Floquet5] was performed for an arbitrary inclination angle and a combination of the longitudinal (along the incline) and orthogonal (perpendicular to the incline) vibrations. However, the results based on linearization of the Navier–Stokes equation were only given for the case of orthogonal harmonic vibration. It was demonstrated that for large frequencies, long gravity driven waves can be strongly suppressed, but cannot be completely eliminated by the vibration. More specifically, in the absence of vibration, the band of unstable wave vectors
![]() $0<k<k_c$
has an upper bound
$0<k<k_c$
has an upper bound
![]() $k_c$
that generally depends on the fluid properties and the inclination angle. When a weak vibration is applied, the value of the cut-off wave vector
$k_c$
that generally depends on the fluid properties and the inclination angle. When a weak vibration is applied, the value of the cut-off wave vector
![]() $k_c$
decreases implying that the long-wave instability is pushed towards larger wavelengths. Later, the linear stability results were verified experimentally [Reference Garih, Julius, Estivalezes and Casalis6, Reference Garih, Strzelecki, Casalis and Estivalezes7] for the case of a liquid layer flowing down a vertical plate.
$k_c$
decreases implying that the long-wave instability is pushed towards larger wavelengths. Later, the linear stability results were verified experimentally [Reference Garih, Julius, Estivalezes and Casalis6, Reference Garih, Strzelecki, Casalis and Estivalezes7] for the case of a liquid layer flowing down a vertical plate.
The interaction between nonlinear gravity-driven solitary waves and shorter Faraday waves on the surface of a liquid film flowing down a slightly inclined plane has been investigated theoretically and experimentally by Maksymov and Pototsky [Reference Maksymov and Pototsky11]. It was demonstrated using sub-millimetre water films that harmonic vibration with frequencies in the range between 30 and 50 Hz decreases the amplitude of long soliton-like surface waves, while the speed of the waves is unaffected by the vibration.
A similar stabilizing effect of vibration was experimentally observed in relation to the Rayleigh–Taylor instability that develops in horizontal liquid films on the underside of a vibrated plate [Reference Hoffmann and Wolf8, Reference Wolf21, Reference Wolf22]. A detailed theoretical analysis of Rayleigh–Taylor unstable horizontal one-layer films under the influence of longitudinal and orthogonal harmonic vibration was conducted using a reduced hydrodynamic model based on the lubrication approximation [Reference Bestehorn1, Reference Sterman-Cohen, Bestehorn and Oron20]. In particular, the ranges of the longitudinal vibration amplitudes and frequencies were found, where the film-rupture was prevented by advection induced by a periodic forcing. For sufficiently large forcing amplitudes, a new inertial rupture mode was detected, while for orthogonal vibrations, nonlinear patterns were found to consist of the mixture of saturated harmonic and subharmonic waves.
The stability and nonlinear dynamics of vibrated multilayered systems are much less studied. It is known that in two-layer films, the so-called zigzag barotropic and varicose thinning modes can be excited. The former corresponds to the in-phase deflections of the liquid–liquid and the liquid–gas interfaces, while the latter is characterized by anti-phase surface deformations. The stability of Faraday waves in horizontal two-layer films has been studied by linearizing Navier–Stokes equations in [Reference Pototsky and Bestehorn13]. It was shown that for any fixed wave vector, the type of the neutrally stable mode may vary over one oscillation period between the zigzag and the varicose types. The interplay between Rayleigh–Taylor and Faraday instabilities has been investigated by considering a two-layered film with a heavier fluid on top in [Reference Bestehorn and Pototsky2, Reference Pototsky and Bestehorn13]. It was concluded that vertical vibration may significantly delay the pinching singularity associated with the rupture of the heavier fluid layer.
Here we use the reduced hydrodynamic model derived by Bestehorn and Pototsky [Reference Bestehorn and Pototsky2] to study the influence of a harmonic vibration on the onset and nonlinear dynamics of solitary gravity-driven waves in two-layer liquid films flowing along a vertical solid plate. In the absence of vibration, the flow in the flat layers is unstable with respect to gravity-driven long-wave perturbations leading to the formation of solitary waves [Reference Pototsky and Maksymov15]. Harmonic vibration is applied perpendicularly to the vertical plate so that the base flow in the flat layers is unchanged in the frame of reference co-moving with the plate. We focus on the nonlinear interaction between the gravity-driven and Faraday waves, and demonstrate the co-existence of multiple stable dynamic states in a certain range of vibration parameters and find hysteresis in a transition between solitary and Faraday waves dominated flow regimes.
2 Horizontally vibrated two-layer film on a solid vertical plate
Consider a film consisting of two immiscible and incompressible fluids with dynamic viscosities
![]() $\mu _i$
, densities
$\mu _i$
, densities
![]() $\rho _i$
and the unperturbed thicknesses
$\rho _i$
and the unperturbed thicknesses
![]() $d_i$
,
$d_i$
,
![]() $i=1,2$
. The first layer is adjacent to a vertical solid plate that oscillates horizontally, as schematically shown in Figures 1(a) and 1(b). The horizontal position of the vertical plate is given by
$i=1,2$
. The first layer is adjacent to a vertical solid plate that oscillates horizontally, as schematically shown in Figures 1(a) and 1(b). The horizontal position of the vertical plate is given by
![]() $z_0=a_0\cos (\omega t)$
, where
$z_0=a_0\cos (\omega t)$
, where
![]() $a_0$
is the displacement amplitude and
$a_0$
is the displacement amplitude and
![]() $\omega $
is the vibration frequency. The surface tension coefficients of the deformable liquid–liquid and the liquid–air interfaces are
$\omega $
is the vibration frequency. The surface tension coefficients of the deformable liquid–liquid and the liquid–air interfaces are
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
, respectively.
$\sigma _2$
, respectively.
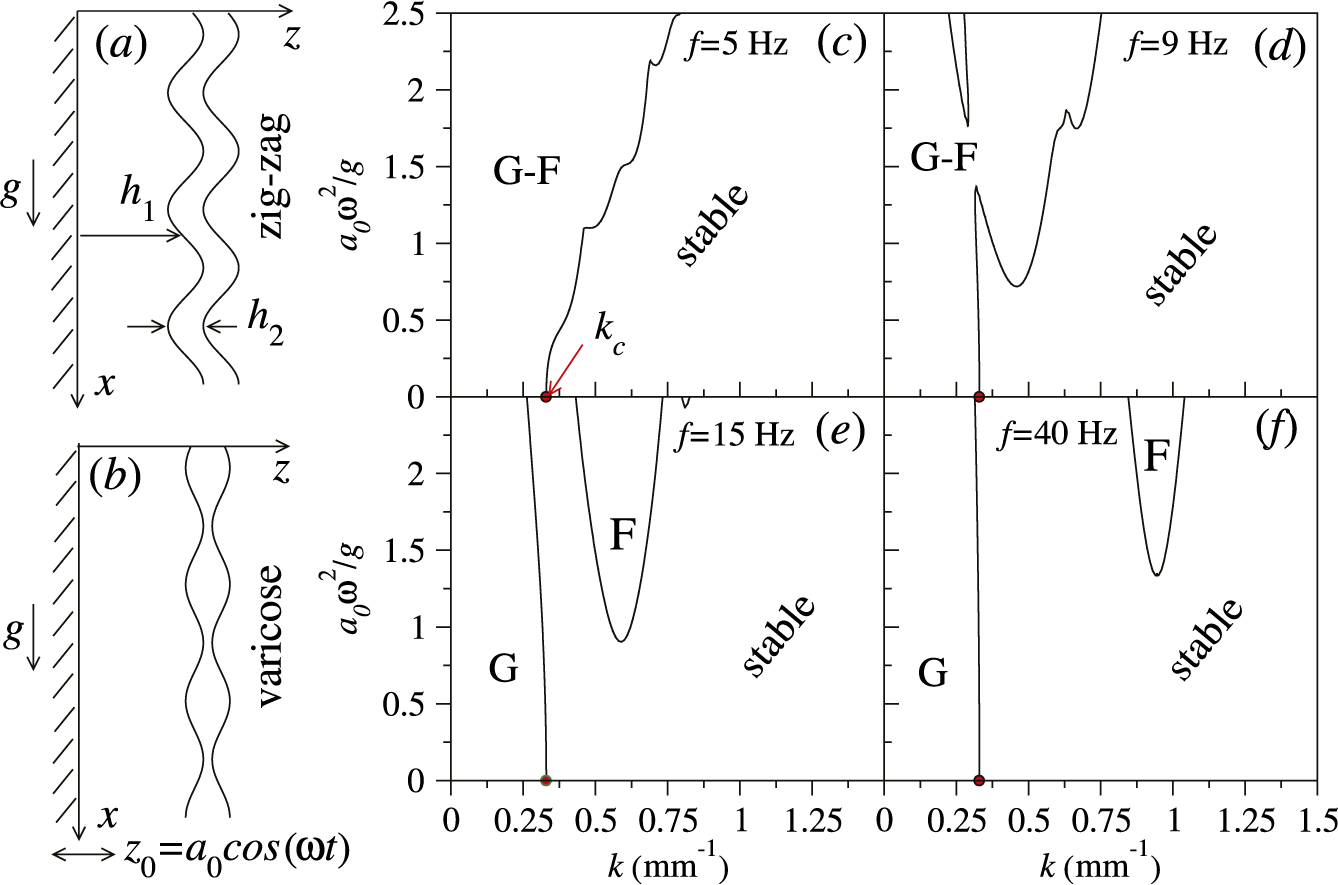
Figure 1 Schematic diagram of a two-layer film with two deformable interfaces flowing down along a solid vertical plate: (a) zigzag and (b) varicose surface deformation modes. Stability diagrams for a 0.5 mm oil film sandwiched between a
![]() $0.5$
mm isopropanol film and an oscillating plate vibrated at (c) 5, (d) 9, (e) 15 and (f) 40 Hz. The system is neutrally stable along the solid lines. The filled circle marks the critical wave vector
$0.5$
mm isopropanol film and an oscillating plate vibrated at (c) 5, (d) 9, (e) 15 and (f) 40 Hz. The system is neutrally stable along the solid lines. The filled circle marks the critical wave vector
![]() $k_c$
of the gravity-driven waves in the absence of vibration. Labels G and F correspond to the gravity- and Faraday-wave dominated parametric regions.
$k_c$
of the gravity-driven waves in the absence of vibration. Labels G and F correspond to the gravity- and Faraday-wave dominated parametric regions.
The reduced hydrodynamic equations in the lubrication approximation that describe the coupled dynamics of the two co-flowing fluids have been derived in [Reference Bestehorn and Pototsky2]. The subsequent analysis is performed in the frame of reference co-moving with the oscillating plate, where the additional time-dependent horizontal acceleration appears due to vibration, and is given by
![]() $a(t)=\ddot z_0=-a_0\omega ^2\cos (\omega t)$
. Reminiscent of the so-called Shkadov model [Reference Shkadov18, Reference Shkadov19] for one-layer films on an inclined surface, the longitudinal flow velocities
$a(t)=\ddot z_0=-a_0\omega ^2\cos (\omega t)$
. Reminiscent of the so-called Shkadov model [Reference Shkadov18, Reference Shkadov19] for one-layer films on an inclined surface, the longitudinal flow velocities
![]() $u_\parallel ^{(i)}(x,z,t)$
in each layer are assumed to be quadratic functions of the horizontal distance from the solid plate z. Navier–Stokes equations for each fluid are simplified in the lubrication approximation by integration over z. The two resulting coupled first-order equations for the longitudinal fluxes
$u_\parallel ^{(i)}(x,z,t)$
in each layer are assumed to be quadratic functions of the horizontal distance from the solid plate z. Navier–Stokes equations for each fluid are simplified in the lubrication approximation by integration over z. The two resulting coupled first-order equations for the longitudinal fluxes
 $$ \begin{align*} q_1=\int_0^{h_1}u_\parallel^{(1)}(z,x,t)\,dz \quad \text{and} \quad q_2=\int_{h_1}^{h_1+h_2}u_\parallel^{(2)}(z,x,t)\,dz \end{align*} $$
$$ \begin{align*} q_1=\int_0^{h_1}u_\parallel^{(1)}(z,x,t)\,dz \quad \text{and} \quad q_2=\int_{h_1}^{h_1+h_2}u_\parallel^{(2)}(z,x,t)\,dz \end{align*} $$
are (see [Reference Bestehorn and Pototsky2, Reference Pototsky and Maksymov15, Reference Pototsky, Oron and Bestehorn16])
 $$ \begin{align} \rho_1 (\partial_t q_1 +\partial_x(\boldsymbol{q}^T \boldsymbol{b}_1 \boldsymbol{q})) &= \mu_1(\boldsymbol{a} \boldsymbol{q})_1+h_1(\sigma_1+\sigma_2)\partial_x^3h_1 +\sigma_2 h_1\partial_x^3h_2\nonumber\\ &\quad -a(t)h_1(\rho_1\partial_xh_1+\rho_2\partial_xh_2) +\rho_1gh_1\,, \end{align} $$
$$ \begin{align} \rho_1 (\partial_t q_1 +\partial_x(\boldsymbol{q}^T \boldsymbol{b}_1 \boldsymbol{q})) &= \mu_1(\boldsymbol{a} \boldsymbol{q})_1+h_1(\sigma_1+\sigma_2)\partial_x^3h_1 +\sigma_2 h_1\partial_x^3h_2\nonumber\\ &\quad -a(t)h_1(\rho_1\partial_xh_1+\rho_2\partial_xh_2) +\rho_1gh_1\,, \end{align} $$
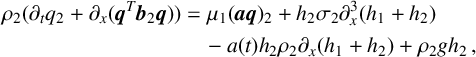 $$ \begin{align} \rho_2 (\partial_t q_2+\partial_x(\boldsymbol{q}^T \boldsymbol{b}_2 \boldsymbol{q})) &= \mu_1(\boldsymbol{a}\boldsymbol{q})_2 +h_2\sigma_2\partial_x^3(h_1+h_2)\nonumber\\ &\quad -a(t)h_2\rho_2\partial_x(h_1+h_2)+\rho_2gh_2\,, \end{align} $$
$$ \begin{align} \rho_2 (\partial_t q_2+\partial_x(\boldsymbol{q}^T \boldsymbol{b}_2 \boldsymbol{q})) &= \mu_1(\boldsymbol{a}\boldsymbol{q})_2 +h_2\sigma_2\partial_x^3(h_1+h_2)\nonumber\\ &\quad -a(t)h_2\rho_2\partial_x(h_1+h_2)+\rho_2gh_2\,, \end{align} $$
where
![]() $\partial _t\equiv {\partial }/{\partial t}$
,
$\partial _t\equiv {\partial }/{\partial t}$
,
![]() $\partial _x\equiv {\partial }/{\partial x}$
,
$\partial _x\equiv {\partial }/{\partial x}$
,
![]() $\boldsymbol {q}=(q_1;q_2)$
is a column
$\boldsymbol {q}=(q_1;q_2)$
is a column
![]() $(2\times 1)$
vector of fluxes,
$(2\times 1)$
vector of fluxes,
![]() $(\cdot )^T$
denotes the transposition,
$(\cdot )^T$
denotes the transposition,
![]() $\boldsymbol {b}_i=\boldsymbol {m}^T\boldsymbol {e}_i \boldsymbol {m}$
, and matrices
$\boldsymbol {b}_i=\boldsymbol {m}^T\boldsymbol {e}_i \boldsymbol {m}$
, and matrices
![]() $\boldsymbol {a}$
,
$\boldsymbol {a}$
,
![]() $\boldsymbol {m}$
and
$\boldsymbol {m}$
and
![]() $\boldsymbol {e}_i$
,
$\boldsymbol {e}_i$
,
![]() $i=1,2$
, are given by
$i=1,2$
, are given by
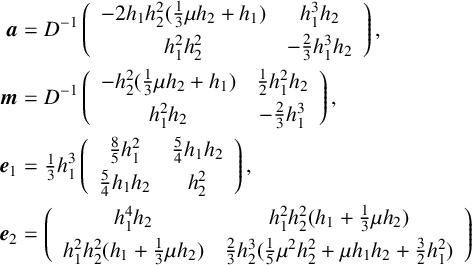 $$ \begin{align*} \boldsymbol{a} &=D^{-1}\left(\begin{array}{cc} -2h_1h_2^2(\tfrac13\mu h_2+h_1)&h_1^3h_2\\[3pt] h_1^2h_2^2&-\tfrac23h_1^3h_2 \end{array}\right),\\ \boldsymbol{m} &=D^{-1}\left(\begin{array}{cc} -h_2^2(\tfrac13\mu h_2+h_1)&\tfrac12h_1^2h_2\\[3pt] h_1^2h_2&-\tfrac23h_1^3 \end{array}\right),\\ \boldsymbol{e}_1 &=\tfrac13h_1^3\left(\begin{array}{cc} \tfrac85h_1^2&\tfrac54h_1h_2\\[3pt] \tfrac54h_1h_2&h_2^2 \end{array}\right),\\ \boldsymbol{e}_2 &=\left(\begin{array}{cc} h_1^4h_2&h_1^2h_2^2(h_1+\tfrac{1}{3}\mu h_2)\\[3pt] h_1^2h_2^2(h_1+\tfrac{1}{3}\mu h_2) &\tfrac{2}{3}h_2^3(\tfrac{1}{5}\mu^2h_2^2 +\mu h_1h_2+\tfrac{3}{2}h_1^2) \end{array}\right) \end{align*} $$
$$ \begin{align*} \boldsymbol{a} &=D^{-1}\left(\begin{array}{cc} -2h_1h_2^2(\tfrac13\mu h_2+h_1)&h_1^3h_2\\[3pt] h_1^2h_2^2&-\tfrac23h_1^3h_2 \end{array}\right),\\ \boldsymbol{m} &=D^{-1}\left(\begin{array}{cc} -h_2^2(\tfrac13\mu h_2+h_1)&\tfrac12h_1^2h_2\\[3pt] h_1^2h_2&-\tfrac23h_1^3 \end{array}\right),\\ \boldsymbol{e}_1 &=\tfrac13h_1^3\left(\begin{array}{cc} \tfrac85h_1^2&\tfrac54h_1h_2\\[3pt] \tfrac54h_1h_2&h_2^2 \end{array}\right),\\ \boldsymbol{e}_2 &=\left(\begin{array}{cc} h_1^4h_2&h_1^2h_2^2(h_1+\tfrac{1}{3}\mu h_2)\\[3pt] h_1^2h_2^2(h_1+\tfrac{1}{3}\mu h_2) &\tfrac{2}{3}h_2^3(\tfrac{1}{5}\mu^2h_2^2 +\mu h_1h_2+\tfrac{3}{2}h_1^2) \end{array}\right) \end{align*} $$
with
 $$ \begin{align*} D=\dfrac29\mu h_1^3h_2^3+\dfrac16h_1^4h_2^2 \quad \text{and} \quad \mu=\dfrac{\mu_1}{\mu_2}.\end{align*} $$
$$ \begin{align*} D=\dfrac29\mu h_1^3h_2^3+\dfrac16h_1^4h_2^2 \quad \text{and} \quad \mu=\dfrac{\mu_1}{\mu_2}.\end{align*} $$
Note that the matrices
![]() $\boldsymbol {e}_i$
and
$\boldsymbol {e}_i$
and
![]() $\boldsymbol {b}_i$
are symmetric. The evolution of the local film thicknesses
$\boldsymbol {b}_i$
are symmetric. The evolution of the local film thicknesses
![]() $h_i$
,
$h_i$
,
![]() $i=1,2$
, is given by two kinematic equations that represent the conservation of the volume of each fluid
$i=1,2$
, is given by two kinematic equations that represent the conservation of the volume of each fluid
Equations (2.1)–(2.3) have been previously used to study Faraday instability in horizontal two-layer films [Reference Bestehorn and Pototsky2, Reference Pototsky and Bestehorn13], the dynamics of an isolated liquid drop of a heavier fluid on top of an immiscible lighter fluid [Reference Pototsky, Oron and Bestehorn16] and the development of solitary waves in falling two-layer films [Reference Pototsky and Maksymov15]. As shown by Pototsky et al. [Reference Pototsky, Oron and Bestehorn16], when films do not flow, (2.1)–(2.3) reduce to the inertialess long wave model of two-layer films [Reference Pototsky, Bestehorn, Merkt and Thiele14] in the parametrization used by Bommer et al. [Reference Bommer, Cartellier, Jachalski, Peschka, Seemann and Wagne3].
While our main goal is to study the interaction of the developing nonlinear rolling waves under the action of horizontal vibration, before doing so, we focus on the linear stability of the base flow in a flat two-layer film with thicknesses
![]() $h_i=d_i$
,
$h_i=d_i$
,
![]() $i=1,2$
. This will enable us to find the smallest possible vibration amplitude at which Faraday waves start developing at a given frequency.
$i=1,2$
. This will enable us to find the smallest possible vibration amplitude at which Faraday waves start developing at a given frequency.
Since we only consider horizontal vibration, the base flow is steady and constant fluxes
![]() $q_i^{(0)}$
can be found from (2.1) by setting
$q_i^{(0)}$
can be found from (2.1) by setting
![]() $h_i=d_i$
,
$h_i=d_i$
,
![]() $i=1,2$
:
$i=1,2$
:
where
![]() $\boldsymbol {a}^{(0)}$
is the matrix
$\boldsymbol {a}^{(0)}$
is the matrix
![]() $\boldsymbol {a}$
with
$\boldsymbol {a}$
with
![]() $h_i=d_i$
,
$h_i=d_i$
,
![]() $i=1,2$
. After inverting the matrix
$i=1,2$
. After inverting the matrix
![]() $\boldsymbol {a}$
, we obtain from (2.4),
$\boldsymbol {a}$
, we obtain from (2.4),
 $$ \begin{align} q_1^{(0)} &=\frac{g\rho_1}{2\mu_1} \bigg(\frac23d_1^3+\frac{\rho_2} {\rho_1}d_1^2d_2\bigg), \end{align} $$
$$ \begin{align} q_1^{(0)} &=\frac{g\rho_1}{2\mu_1} \bigg(\frac23d_1^3+\frac{\rho_2} {\rho_1}d_1^2d_2\bigg), \end{align} $$
 $$ \begin{align} q_2^{(0)} &= \frac{g\rho_1}{2\mu_1}\bigg(d_1^2d_2+\frac{2\rho_2}{\rho_1} \bigg(d_2^3\frac{\mu_1}{3\mu_2}+d_1d_2^2\bigg)\bigg). \end{align} $$
$$ \begin{align} q_2^{(0)} &= \frac{g\rho_1}{2\mu_1}\bigg(d_1^2d_2+\frac{2\rho_2}{\rho_1} \bigg(d_2^3\frac{\mu_1}{3\mu_2}+d_1d_2^2\bigg)\bigg). \end{align} $$
Fluxes (2.5) and (2.6) coincide with the those in a steady flow in a free-falling two-layer flat film derived earlier in the absence of vibration [Reference Kao9, Reference Kao10].
Next, we linearize (2.1)–(2.3) about the steady state by adding infinitesimal disturbances
![]() $\tilde {q}_i$
and
$\tilde {q}_i$
and
![]() $\tilde {h}_i$
of the fluxes and film thicknesses, respectively, to it:
$\tilde {h}_i$
of the fluxes and film thicknesses, respectively, to it:
![]() $q_i=q_i^{(0)}+\tilde {q}_i$
,
$q_i=q_i^{(0)}+\tilde {q}_i$
,
![]() $h_i=d_i+\tilde h_i$
,
$h_i=d_i+\tilde h_i$
,
![]() $i=1,2$
. Fluxes
$i=1,2$
. Fluxes
![]() $q_i$
are subsequently eliminated by differentiating (2.3) with respect to time and (2.1) with respect to x. The resulting linear system of two coupled Mathieu equations [Reference Mathieu12] for time-dependent perturbations of the local film thicknesses
$q_i$
are subsequently eliminated by differentiating (2.3) with respect to time and (2.1) with respect to x. The resulting linear system of two coupled Mathieu equations [Reference Mathieu12] for time-dependent perturbations of the local film thicknesses
![]() $\tilde h_i(t)$
is then written as
$\tilde h_i(t)$
is then written as
 $$ \begin{align} \partial_{tt}\begin{bmatrix}\tilde h_1\\\tilde h_2\end{bmatrix} =[\boldsymbol{A}\partial_t+\boldsymbol{B}] \begin{bmatrix}\tilde h_1\\ \tilde h_2\end{bmatrix}, \end{align} $$
$$ \begin{align} \partial_{tt}\begin{bmatrix}\tilde h_1\\\tilde h_2\end{bmatrix} =[\boldsymbol{A}\partial_t+\boldsymbol{B}] \begin{bmatrix}\tilde h_1\\ \tilde h_2\end{bmatrix}, \end{align} $$
where matrices
![]() $\boldsymbol {A}$
and
$\boldsymbol {A}$
and
![]() $\boldsymbol {B}$
are given by
$\boldsymbol {B}$
are given by
 $$ \begin{align*} \boldsymbol{A}=-\frac{\mu_1}{\rho_1} \begin{bmatrix} a_{11}^{(0)}& a_{12}^{(0)}\\ \rho a_{21}^{(0)}& \rho a_{22}^{(0)}\\ \end{bmatrix} +2ik \begin{bmatrix} (\boldsymbol{b}_1^{(0)} \boldsymbol{q}^{(0)})_1 & (\boldsymbol{b}_1^{(0)} \boldsymbol{q}^{(0)})_2 \\ (\boldsymbol{b}_2^{(0)} \boldsymbol{q}^{(0)})_1 & (\boldsymbol{b}_2^{(0)} \boldsymbol{q}^{(0)})_2 \\ \end{bmatrix} \end{align*} $$
$$ \begin{align*} \boldsymbol{A}=-\frac{\mu_1}{\rho_1} \begin{bmatrix} a_{11}^{(0)}& a_{12}^{(0)}\\ \rho a_{21}^{(0)}& \rho a_{22}^{(0)}\\ \end{bmatrix} +2ik \begin{bmatrix} (\boldsymbol{b}_1^{(0)} \boldsymbol{q}^{(0)})_1 & (\boldsymbol{b}_1^{(0)} \boldsymbol{q}^{(0)})_2 \\ (\boldsymbol{b}_2^{(0)} \boldsymbol{q}^{(0)})_1 & (\boldsymbol{b}_2^{(0)} \boldsymbol{q}^{(0)})_2 \\ \end{bmatrix} \end{align*} $$
and
 $$ \begin{align*} \boldsymbol{B}(t) &=k^2\begin{bmatrix} (\boldsymbol{q}^{(0)})^T \partial_{d_1}\boldsymbol{b}_1^{(0)} \boldsymbol{q}^{(0)} &(\boldsymbol{q}^{(0)})^T \partial_{d_2}\boldsymbol{b}_1^{(0)} \boldsymbol{q}^{(0)}\\ (\boldsymbol{q}^{(0)})^T \partial_{d_1}\boldsymbol{b}_2^{(0)} \boldsymbol{q}^{(0)} &(\boldsymbol{q}^{(0)})^T \partial_{d_2}\boldsymbol{b}_2^{(0)} \boldsymbol{q}^{(0)} \end{bmatrix}\\[.2cm] &\quad +\frac{ik\mu_1}{\rho_1} \begin{bmatrix} (\partial_{d_1}\boldsymbol{a}^{(0)} \boldsymbol{q}^{(0)})_1 &(\partial_{d_2}\boldsymbol{a}^{(0)} \boldsymbol{q}^{(0)})_1\\ \rho(\partial_{d_1}\boldsymbol{a}^{(0)} \boldsymbol{q}^{(0)})_2 &\rho(\partial_{d_2}\boldsymbol{a}^{(0)} \boldsymbol{q}^{(0)})_2 \end{bmatrix} +ikg\begin{bmatrix}1&0\\0&1\end{bmatrix}\\[.2cm] &\quad +\frac{k^4}{\rho_1} \begin{bmatrix} d_1(\sigma_1+\sigma_2)&d_1\sigma_2\\ \rho d_2\sigma_2&\rho d_2\sigma_2 \end{bmatrix}+a(t)\frac{k^2}{\rho} \begin{bmatrix} \rho d_1&d_1\\ \rho d_2&\rho d_2 \end{bmatrix}, \end{align*} $$
$$ \begin{align*} \boldsymbol{B}(t) &=k^2\begin{bmatrix} (\boldsymbol{q}^{(0)})^T \partial_{d_1}\boldsymbol{b}_1^{(0)} \boldsymbol{q}^{(0)} &(\boldsymbol{q}^{(0)})^T \partial_{d_2}\boldsymbol{b}_1^{(0)} \boldsymbol{q}^{(0)}\\ (\boldsymbol{q}^{(0)})^T \partial_{d_1}\boldsymbol{b}_2^{(0)} \boldsymbol{q}^{(0)} &(\boldsymbol{q}^{(0)})^T \partial_{d_2}\boldsymbol{b}_2^{(0)} \boldsymbol{q}^{(0)} \end{bmatrix}\\[.2cm] &\quad +\frac{ik\mu_1}{\rho_1} \begin{bmatrix} (\partial_{d_1}\boldsymbol{a}^{(0)} \boldsymbol{q}^{(0)})_1 &(\partial_{d_2}\boldsymbol{a}^{(0)} \boldsymbol{q}^{(0)})_1\\ \rho(\partial_{d_1}\boldsymbol{a}^{(0)} \boldsymbol{q}^{(0)})_2 &\rho(\partial_{d_2}\boldsymbol{a}^{(0)} \boldsymbol{q}^{(0)})_2 \end{bmatrix} +ikg\begin{bmatrix}1&0\\0&1\end{bmatrix}\\[.2cm] &\quad +\frac{k^4}{\rho_1} \begin{bmatrix} d_1(\sigma_1+\sigma_2)&d_1\sigma_2\\ \rho d_2\sigma_2&\rho d_2\sigma_2 \end{bmatrix}+a(t)\frac{k^2}{\rho} \begin{bmatrix} \rho d_1&d_1\\ \rho d_2&\rho d_2 \end{bmatrix}, \end{align*} $$
where k denotes the wave vector of the perturbation,
![]() $\rho ={\rho _1}/{\rho _2}$
and superscript
$\rho ={\rho _1}/{\rho _2}$
and superscript
![]() $(0)$
indicates that the corresponding matrices are obtained by replacing
$(0)$
indicates that the corresponding matrices are obtained by replacing
![]() $h_i$
with
$h_i$
with
![]() $d_i$
.
$d_i$
.
According to Floquet theory [Reference Floquet5], the general solution of (2.7) is given by
where
![]() $F_i(t)$
are some complex-valued periodic functions with the period of forcing
$F_i(t)$
are some complex-valued periodic functions with the period of forcing
![]() ${T={2\pi }/{\omega }}$
and
${T={2\pi }/{\omega }}$
and
![]() $\lambda $
is a complex Floquet exponent. For any given wave vector k, the solution is linearly unstable if
$\lambda $
is a complex Floquet exponent. For any given wave vector k, the solution is linearly unstable if
![]() $\Re \{\lambda \}>0$
. The real and imaginary parts of the Floquet exponent are found from the monodromy matrix of universal solutions
$\Re \{\lambda \}>0$
. The real and imaginary parts of the Floquet exponent are found from the monodromy matrix of universal solutions
![]() $\boldsymbol {M}$
as
$\boldsymbol {M}$
as
![]() $\Re \{\lambda \}=(\ln |\Lambda | )/T$
and
$\Re \{\lambda \}=(\ln |\Lambda | )/T$
and
![]() $\Im \{\lambda \}=({\arg }(\Lambda )) /T$
, where
$\Im \{\lambda \}=({\arg }(\Lambda )) /T$
, where
![]() $\Lambda $
is an eigenvalue of
$\Lambda $
is an eigenvalue of
![]() $\boldsymbol {M}$
and
$\boldsymbol {M}$
and
![]() $\arg (\cdot )$
denotes the argument of a complex number. Note that the imaginary part of Floquet exponents is determined up to
$\arg (\cdot )$
denotes the argument of a complex number. Note that the imaginary part of Floquet exponents is determined up to
![]() ${2\pi n}\text {i} /T$
, where n is an arbitrary integer. To obtain the monodromy matrix, we write (2.7) as a system of four first-order complex-valued equations and then integrate it over one period T for four different initial conditions using the fourth-order Runge–Kutta method. The initial conditions are given by the columns of the
${2\pi n}\text {i} /T$
, where n is an arbitrary integer. To obtain the monodromy matrix, we write (2.7) as a system of four first-order complex-valued equations and then integrate it over one period T for four different initial conditions using the fourth-order Runge–Kutta method. The initial conditions are given by the columns of the
![]() $4\times 4$
identity matrix. The resulting solutions after one period T are stored as columns of the
$4\times 4$
identity matrix. The resulting solutions after one period T are stored as columns of the
![]() $4\times 4$
monodromy matrix
$4\times 4$
monodromy matrix
![]() $\boldsymbol {M}$
. The eigenvalues of
$\boldsymbol {M}$
. The eigenvalues of
![]() $\boldsymbol {M}$
are found numerically. We apply the above procedure to obtain the standard stability diagram in the parameter space
$\boldsymbol {M}$
are found numerically. We apply the above procedure to obtain the standard stability diagram in the parameter space
![]() $({a_0\omega ^2}/{g},k)$
for fixed vibration frequency
$({a_0\omega ^2}/{g},k)$
for fixed vibration frequency
![]() $\omega $
.
$\omega $
.
As an example, we consider a layer of oil with density
![]() $\rho _{1} = 1850$
kg
$\rho _{1} = 1850$
kg
![]() ${\cdot }\mbox {m}^{-3}$
and dynamic viscosity
${\cdot }\mbox {m}^{-3}$
and dynamic viscosity
![]() $\mu _1=0.026$
Pa
$\mu _1=0.026$
Pa
![]() $\cdot $
s sandwiched between the solid plate and a layer of isopropanol with the density
$\cdot $
s sandwiched between the solid plate and a layer of isopropanol with the density
![]() $\rho _2=785$
kg
$\rho _2=785$
kg
![]() $\cdot \mbox {m}^{-3}$
and dynamic viscosity
$\cdot \mbox {m}^{-3}$
and dynamic viscosity
![]() $\mu _2=0.0018$
Pa
$\mu _2=0.0018$
Pa
![]() $\cdot $
s. The interfacial (liquid–liquid) and surface (liquid–air) tension coefficients are
$\cdot $
s. The interfacial (liquid–liquid) and surface (liquid–air) tension coefficients are
![]() $\sigma _1=0.0063$
N
$\sigma _1=0.0063$
N
![]() $\cdot \mbox {m}^{-1}$
and
$\cdot \mbox {m}^{-1}$
and
![]() $\sigma _2=0.024$
N
$\sigma _2=0.024$
N
![]() $\cdot \mbox {m}^{-1}$
, respectively. The same combination of fluids has been used in earlier experiments with vertically vibrated liquid drops floating on the surface of another immiscible fluid [Reference Pucci, Fort, Ben Amar and Couder17]. The average thicknesses of the layers are chosen to be
$\cdot \mbox {m}^{-1}$
, respectively. The same combination of fluids has been used in earlier experiments with vertically vibrated liquid drops floating on the surface of another immiscible fluid [Reference Pucci, Fort, Ben Amar and Couder17]. The average thicknesses of the layers are chosen to be
![]() $d_1=0.5$
mm and
$d_1=0.5$
mm and
![]() $d_1+d_2=1$
mm.
$d_1+d_2=1$
mm.
The stability diagrams for a flat two-layer film vibrated with different frequencies f and amplitudes
![]() $a_0$
are shown in Figure 1(c)–1(f). In the absence of vibration, the system is unstable with respect to gravity-driven waves with the wave vectors below some critical cut-off
$a_0$
are shown in Figure 1(c)–1(f). In the absence of vibration, the system is unstable with respect to gravity-driven waves with the wave vectors below some critical cut-off
![]() $k_c$
as seen in Figure 1(c). It is noteworthy that a weak low-frequency vibration with
$k_c$
as seen in Figure 1(c). It is noteworthy that a weak low-frequency vibration with
![]() $f=5$
Hz leads to an increase in the value of
$f=5$
Hz leads to an increase in the value of
![]() $k_c$
rendering the vibrated system less stable. In contrast, as the frequency increases above
$k_c$
rendering the vibrated system less stable. In contrast, as the frequency increases above
![]() $f=9$
Hz,
$f=9$
Hz,
![]() $k_c$
decreases for small values of
$k_c$
decreases for small values of
![]() $a_0$
and long waves are suppressed. This effect is similar to the observed suppression of Rayleigh–Taylor instability in horizontal one- and two-layer liquid films [Reference Bestehorn1, Reference Sterman-Cohen, Bestehorn and Oron20–Reference Wolf22]. In addition to the reduction of
$a_0$
and long waves are suppressed. This effect is similar to the observed suppression of Rayleigh–Taylor instability in horizontal one- and two-layer liquid films [Reference Bestehorn1, Reference Sterman-Cohen, Bestehorn and Oron20–Reference Wolf22]. In addition to the reduction of
![]() $k_c$
for
$k_c$
for
![]() $f>9$
Hz, the region of gravity-dominated instability becomes separated from the region marked by “Faraday” in Figure 1(c), where Faraday instability sets.
$f>9$
Hz, the region of gravity-dominated instability becomes separated from the region marked by “Faraday” in Figure 1(c), where Faraday instability sets.
In a two-layer film with two deformable interfaces, there exist two distinct mode types associated with the in-phase and anti-phase deflections of the liquid–liquid and the liquid–air interfaces. The in-phase deflections correspond to the zigzag barotropic mode and the anti-phase surface deformations are associated with the varicose thinning mode as schematically shown in Figures 1(a) and 1(b). As shown by Pototsky and Bestehorn [Reference Pototsky and Bestehorn13], the mode type generally depends on time in agreement with the general solution (2.8). However, for a certain range of vibration parameters, the dynamics is largely dominated by one of the two mode types. Thus, for the parameters in Figure 1(c)–1(f), the asymmetric zigzag mode dominates with large liquid–air interface deflections and an almost flat liquid–liquid interface.
Our main goal is to study the nonlinear interaction between the long gravity-driven waves and shorter Faraday waves. This scenario can be best realized when the region of the gravity-driven instability in the
![]() $({a_0\omega ^2}/{g},k)$
plane is well separated from that of Faraday instability. Therefore, we set
$({a_0\omega ^2}/{g},k)$
plane is well separated from that of Faraday instability. Therefore, we set
![]() $f=40$
Hz and numerically solve (2.1)–(2.3) in the periodic domain
$f=40$
Hz and numerically solve (2.1)–(2.3) in the periodic domain
![]() $(-L\leq x\leq L)$
, where sufficiently large
$(-L\leq x\leq L)$
, where sufficiently large
![]() $L=3$
m is chosen to study the dynamics of solitary waves. Figure 2 illustrates three temporal surface evolution scenarios for different values of the vibration acceleration amplitude. In the absence of vibration, unstable gravity-driven waves gradually develop and grow by means of inelastic wave collision as revealed by Pototsky and Maksymov [Reference Pototsky and Maksymov15]. The wave growth is arrested when each wave reaches a near homoclinic solitary-like solution, as shown in Figure 2(1)–2(4). Our numerical simulations indicate that in the considered cases, these solitary waves are stable and several of them can coexist depending on the initial conditions. However, a full spatiotemporal stability study of nonlinear rolling waves has not been undertaken here because it would require a lengthy analysis of the dynamic equations 2.1–2.3 linearized about the nonlinear travelling pulsating solitary wave in the co-moving frame of reference. Presenting it would require more journal space than available for this short contribution.
$L=3$
m is chosen to study the dynamics of solitary waves. Figure 2 illustrates three temporal surface evolution scenarios for different values of the vibration acceleration amplitude. In the absence of vibration, unstable gravity-driven waves gradually develop and grow by means of inelastic wave collision as revealed by Pototsky and Maksymov [Reference Pototsky and Maksymov15]. The wave growth is arrested when each wave reaches a near homoclinic solitary-like solution, as shown in Figure 2(1)–2(4). Our numerical simulations indicate that in the considered cases, these solitary waves are stable and several of them can coexist depending on the initial conditions. However, a full spatiotemporal stability study of nonlinear rolling waves has not been undertaken here because it would require a lengthy analysis of the dynamic equations 2.1–2.3 linearized about the nonlinear travelling pulsating solitary wave in the co-moving frame of reference. Presenting it would require more journal space than available for this short contribution.
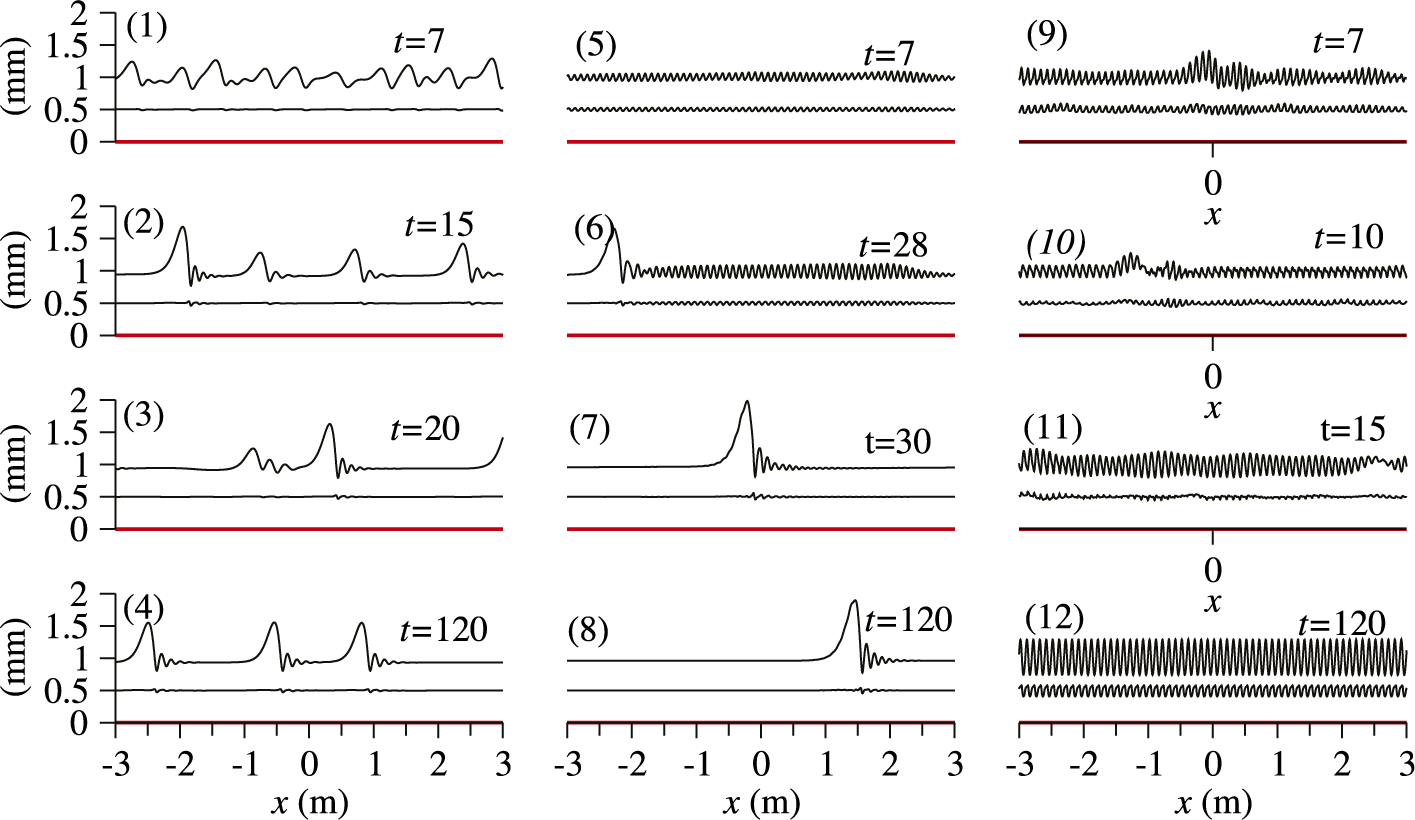
Figure 2 Temporal evolution of oil/isopropanol film with parameters as in Figure 1 vibrated at
![]() ${f=40}$
Hz with three different amplitudes: (1)–(4)
${f=40}$
Hz with three different amplitudes: (1)–(4)
![]() $a_0=0$
; (5)–(8)
$a_0=0$
; (5)–(8)
![]() $a_0\omega ^2=2.0g$
; (9)–(12)
$a_0\omega ^2=2.0g$
; (9)–(12)
![]() $a_0\omega ^2=2.5g$
. Time (seconds) is given in the legend in each panel.
$a_0\omega ^2=2.5g$
. Time (seconds) is given in the legend in each panel.
A weak vibration does not have a noticeable effect on the development of the solitary waves (details not shown here). However, when the vibration amplitude reaches the critical value of approximately
![]() $a_0\omega ^2=2.0g$
, the system exhibits much more complex dynamics. At an early stage, short Faraday waves dominate the evolution, as shown in Figure 2(5). However, Faraday waves become modulated by longer gravity-driven counterparts that grow and eventually suppress Faraday waves at later times, as shown in Figure 2(8). When the vibration amplitude is increased to
$a_0\omega ^2=2.0g$
, the system exhibits much more complex dynamics. At an early stage, short Faraday waves dominate the evolution, as shown in Figure 2(5). However, Faraday waves become modulated by longer gravity-driven counterparts that grow and eventually suppress Faraday waves at later times, as shown in Figure 2(8). When the vibration amplitude is increased to
![]() $a_0\omega ^2=2.5g$
, the gravity-driven waves are completely suppressed by Faraday ones, as seen in Figure 2(9)–2(12). In all cases, a highly asymmetric zigzag barotropic mode with a strongly deformed liquid–air interface and a weakly deformed liquid–liquid interface dominates the instability patterns.
$a_0\omega ^2=2.5g$
, the gravity-driven waves are completely suppressed by Faraday ones, as seen in Figure 2(9)–2(12). In all cases, a highly asymmetric zigzag barotropic mode with a strongly deformed liquid–air interface and a weakly deformed liquid–liquid interface dominates the instability patterns.
To gain deeper understanding of how the nonlinear behaviour of the system changes with
![]() $a_0$
, we set
$a_0$
, we set
![]() $f=40$
Hz and employ the continuation procedure to find multiple stable dynamic states for different values of
$f=40$
Hz and employ the continuation procedure to find multiple stable dynamic states for different values of
![]() $a_0$
. We solve (2.1)–(2.3) over the time interval of
$a_0$
. We solve (2.1)–(2.3) over the time interval of
![]() $2$
min for the fixed vibration amplitude. Subsequently, the value of
$2$
min for the fixed vibration amplitude. Subsequently, the value of
![]() $a_0\omega ^2$
is either increased or decreased by a small increment and the system is further integrated over the time interval of
$a_0\omega ^2$
is either increased or decreased by a small increment and the system is further integrated over the time interval of
![]() $2$
min without resetting the initial conditions. We use this continuation protocol to scan the interval of vibration amplitudes
$2$
min without resetting the initial conditions. We use this continuation protocol to scan the interval of vibration amplitudes
![]() $0\leq a_0\omega ^2\leq 3g$
. The time-averaged amplitude
$0\leq a_0\omega ^2\leq 3g$
. The time-averaged amplitude
![]() $\langle \text {ampl}\rangle $
of the stable dynamical state reached after 2 min is shown in Figure 3 as a function of
$\langle \text {ampl}\rangle $
of the stable dynamical state reached after 2 min is shown in Figure 3 as a function of
![]() ${a_0\omega ^2}/{g}$
. Arrows indicate abrupt transitions between different dynamic states associated with gravity driven and Faraday waves. Both regimes coexist in the interval of the vibration amplitude
${a_0\omega ^2}/{g}$
. Arrows indicate abrupt transitions between different dynamic states associated with gravity driven and Faraday waves. Both regimes coexist in the interval of the vibration amplitude
![]() $2g\leq a_0\omega ^2\leq 2.5g$
giving rise to hysteresis: the gravity-driven waves dominate for
$2g\leq a_0\omega ^2\leq 2.5g$
giving rise to hysteresis: the gravity-driven waves dominate for
![]() $a_0\omega ^2\leq 2.5g$
in the continuation protocol with gradually increasing amplitude and Faraday waves prevail for
$a_0\omega ^2\leq 2.5g$
in the continuation protocol with gradually increasing amplitude and Faraday waves prevail for
![]() $a_0\omega ^2\geq 2g$
when the amplitude is gradually decreasing. There exist several stable gravity-driven wave states characterized by the number of solitary-like waves in the domain. The state with the largest average amplitude
$a_0\omega ^2\geq 2g$
when the amplitude is gradually decreasing. There exist several stable gravity-driven wave states characterized by the number of solitary-like waves in the domain. The state with the largest average amplitude
![]() $\langle \text {ampl}\rangle $
has a single solitary wave followed by the states with two and three stable identical waves that travel with identical speeds and, consequently, remain separated. As the vibration amplitude increases above
$\langle \text {ampl}\rangle $
has a single solitary wave followed by the states with two and three stable identical waves that travel with identical speeds and, consequently, remain separated. As the vibration amplitude increases above
![]() $2.5g$
, Faraday waves become visibly modulated by the second wave with a much longer wavelength.
$2.5g$
, Faraday waves become visibly modulated by the second wave with a much longer wavelength.
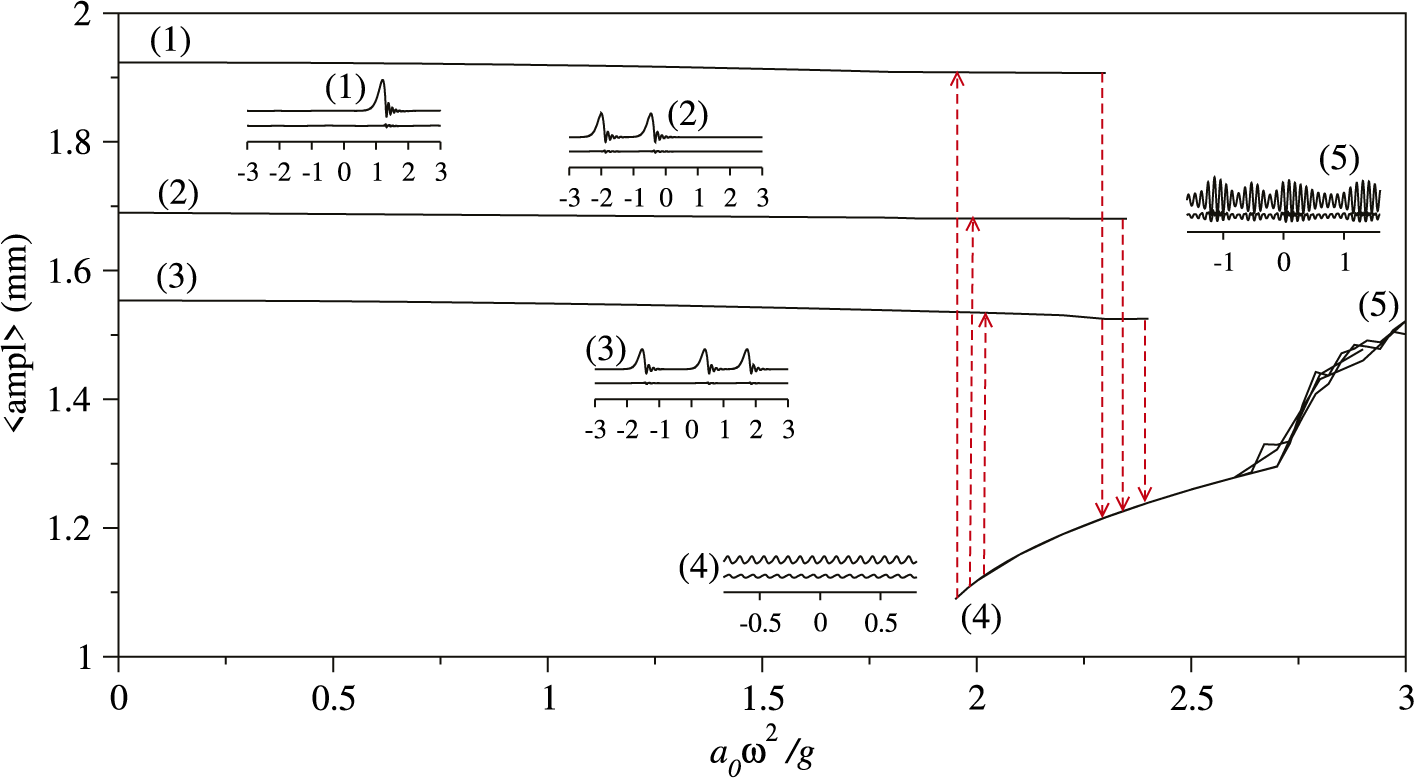
Figure 3 Oil/isopropanol film with parameters as in Figure 1 vibrated at
![]() $f=40$
Hz. The average amplitude
$f=40$
Hz. The average amplitude
![]() $\langle \text {ampl}\rangle $
of the stable dynamical state reached at different vibration amplitudes. Arrows indicate jumps between the gravity driven solitary waves and Faraday waves. Insets (1)–(5) show typical instantaneous wave profiles for the corresponding solution branches.
$\langle \text {ampl}\rangle $
of the stable dynamical state reached at different vibration amplitudes. Arrows indicate jumps between the gravity driven solitary waves and Faraday waves. Insets (1)–(5) show typical instantaneous wave profiles for the corresponding solution branches.
3 Conclusion
We have studied the effect of a harmonic vibration on the onset and nonlinear dynamics of surface waves in vertically flowing two-layer liquid films adjacent to a horizontally vibrated solid plate. In sub-millimetre-thick films, a weak vibration with a frequency below several Hertz leads to an expansion of the unstable band of wave vectors associated with the gravity-driven instability on the surface of a flat two-layer film. As a result, the onset of the gravity-driven waves is aided by the low-frequency vibration. As the frequency is increased above 5–10 Hz, the effect of a weak vibration is reversed. In this frequency range, the vibration suppresses gravity-driven instability by reducing the bandwidth of the unstable wave vectors. Increasing the frequency even further leads to the separation of the wave vector bands, where gravity-driven instability dominates the linear stage of the system dynamics from those where Faraday instability prevails.
The competition between nonlinear gravity-driven and Faraday waves leads to complex flow patterns featuring multiple stable dynamic states dominated by long solitary waves propagating down the plate, or by shorter Faraday waves with the amplitude modulated on a longer scale. The selection of the final dynamical state can be robustly controlled by tuning the vibration amplitude and frequency. The regime featuring long solitary waves prevails at a relatively weak vibration. Here, several stable states can be found with one, two or more identical solitary waves travelling down the plate with the same speed. When the vibration amplitude is slowly increased at a fixed frequency, an abrupt transition from solitary to Faraday waves occurs. This scenario is reversed when the vibration amplitude is gradually decreased. Both regimes can coexist in a certain range of vibration amplitudes giving rise to a hysteresis.
From the point of view of a bifurcation analysis, the presence of hysteresis can be linked to a sub-critical bifurcation of a quasi-periodic solution. Indeed, any travelling wave subjected to harmonic vibration and propagating in a spatially periodic domain can be associated with a quasi-period solution in an infinite-definitional phase space. The quasi-periodicity is characterized by two distinct and possibly incommensurate time scales: the longer one corresponds to the time required for the wave to travel over the length of the domain and the shorter time scale is associated with vibration. Therefore, any such travelling oscillating wave corresponds to the motion on a torus in an infinite-definitional phase space. Our numerical results show that two stable tori may coexist for a certain range of vibration parameters. Most importantly, the observed hysteresis indicates that the transition from one torus to another occurs via a sub-critical bifurcation, which necessarily implies the existence of another unstable torus. The latter is most likely associated with a mixed dynamic state featuring a combination of solitary and Faraday waves.













