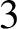Refine search
Actions for selected content:
5 results
A NOTE ON THE FINITELY GENERATED FIXED SUBGROUP PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 530-540
- Print publication:
- June 2025
-
- Article
- Export citation
Geodesic planes in geometrically finite acylindrical
 $3$-manifolds
$3$-manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 514-553
- Print publication:
- February 2022
-
- Article
- Export citation
QUASICONVEXITY OF BANDS IN HYPERBOLIC 3-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 167-185
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
UNKNOTTING TUNNELS, BRACELETS AND THE ELDER SIBLING PROPERTY FOR HYPERBOLIC 3-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 1-19
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
CUSP DENSITIES OF HYPERBOLIC 3-MANIFOLDS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 45 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 17 June 2002, pp. 277-284
-
- Article
-
- You have access
- Export citation