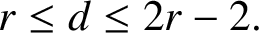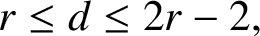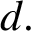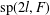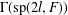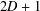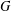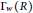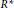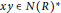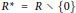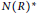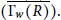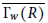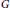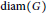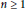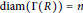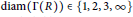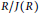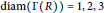Refine search
Actions for selected content:
38 results
Bounds on some geometric functionals of high dimensional Brownian convex hulls and their inverse processes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the perimeter, diameter and circumradius of ordinary hyperbolic reduced polygons
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 February 2025, pp. 950-965
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELEMENTARY PROOFS OF THE DIAMETER BOUNDS FOR POWER GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 505-508
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Network Metrics
- from Part I - A Brief Guide to Network Science
-
- Book:
- Behavioral Network Science
- Published online:
- 08 November 2024
- Print publication:
- 19 December 2024, pp 24-45
-
- Chapter
- Export citation
7 - Diameter
-
- Book:
- Polytopes and Graphs
- Published online:
- 14 March 2024
- Print publication:
- 21 March 2024, pp 305-339
-
- Chapter
- Export citation
8 - Small-World Phenomena in Preferential Attachment Models
- from Part III - Small-World Properties of Random Graphs
-
- Book:
- Random Graphs and Complex Networks
- Published online:
- 08 February 2024
- Print publication:
- 08 February 2024, pp 326-380
-
- Chapter
- Export citation
7 - Small-World Phenomena in Configuration Models
- from Part III - Small-World Properties of Random Graphs
-
- Book:
- Random Graphs and Complex Networks
- Published online:
- 08 February 2024
- Print publication:
- 08 February 2024, pp 289-325
-
- Chapter
- Export citation
6 - Small-World Phenomena in Inhomogeneous Random Graphs
- from Part III - Small-World Properties of Random Graphs
-
- Book:
- Random Graphs and Complex Networks
- Published online:
- 08 February 2024
- Print publication:
- 08 February 2024, pp 245-288
-
- Chapter
- Export citation
9 - Extreme Characteristics
- from Part II - Erdős–Rényi–Gilbert Model
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 111-124
-
- Chapter
- Export citation
THE DIAMETER AND RADIUS OF RADIALLY MAXIMAL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 11 January 2021, pp. 196-202
- Print publication:
- October 2021
-
- Article
- Export citation
Flooding and diameter in general weighted random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 956-980
- Print publication:
- September 2020
-
- Article
- Export citation
SMALL-WORLD EFFECT IN GEOGRAPHICAL ATTACHMENT NETWORKS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 12 September 2019, pp. 276-296
-
- Article
- Export citation
DIAMETER OF COMMUTING GRAPHS OF SYMPLECTIC ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 04 June 2019, pp. 419-427
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Diameter, Decomposability, and Minkowski Sums of Polytopes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 741-755
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
ON THE TOTAL DISTANCE AND DIAMETER OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 14-17
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Correlations among the mineralogical and physical properties of halloysite nanotubes (HNTs)
-
- Journal:
- Clay Minerals / Volume 51 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 02 January 2018, pp. 325-350
-
- Article
- Export citation
The Weakly Nilpotent Graph of a Commutative Ring
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 2 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 319-328
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
A FEW FAMILIES OF CAYLEY GRAPHS AND THEIR EFFICIENCY AS COMMUNICATION NETWORKS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 518-520
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Co-maximal Graphs of Subgroups of Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 12-25
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
On the Diameter of Unitary Cayley Graphs of Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 3 / 01 September 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 652-660
- Print publication:
- 01 September 2016
-
- Article
-
- You have access
- Export citation