No CrossRef data available.
Article contents
DIAMETER OF COMMUTING GRAPHS OF SYMPLECTIC ALGEBRAS
Published online by Cambridge University Press: 04 June 2019
Abstract
Let 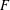 $F$ be an algebraically closed field of characteristic
$F$ be an algebraically closed field of characteristic 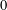 $0$ and let
$0$ and let 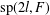 $\operatorname{sp}(2l,F)$ be the rank
$\operatorname{sp}(2l,F)$ be the rank 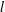 $l$ symplectic algebra of all
$l$ symplectic algebra of all 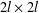 $2l\times 2l$ matrices
$2l\times 2l$ matrices 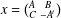 $x=\big(\!\begin{smallmatrix}A & B\\ C & -A^{t}\end{smallmatrix}\!\big)$ over
$x=\big(\!\begin{smallmatrix}A & B\\ C & -A^{t}\end{smallmatrix}\!\big)$ over 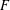 $F$, where
$F$, where 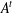 $A^{t}$ is the transpose of
$A^{t}$ is the transpose of 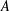 $A$ and
$A$ and 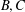 $B,C$ are symmetric matrices of order
$B,C$ are symmetric matrices of order 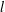 $l$. The commuting graph
$l$. The commuting graph 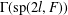 $\unicode[STIX]{x1D6E4}(\operatorname{sp}(2l,F))$ of
$\unicode[STIX]{x1D6E4}(\operatorname{sp}(2l,F))$ of 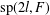 $\operatorname{sp}(2l,F)$ is a graph whose vertex set consists of all nonzero elements in
$\operatorname{sp}(2l,F)$ is a graph whose vertex set consists of all nonzero elements in 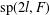 $\operatorname{sp}(2l,F)$ and two distinct vertices
$\operatorname{sp}(2l,F)$ and two distinct vertices  $x$ and
$x$ and 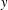 $y$ are adjacent if and only if
$y$ are adjacent if and only if 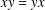 $xy=yx$. We prove that the diameter of
$xy=yx$. We prove that the diameter of 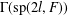 $\unicode[STIX]{x1D6E4}(\operatorname{sp}(2l,F))$ is
$\unicode[STIX]{x1D6E4}(\operatorname{sp}(2l,F))$ is 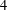 $4$ when
$4$ when 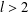 $l>2$.
$l>2$.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 419 - 427
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
Financially supported by the National Natural Science Foundation of China (Grant Nos. 11671164, 11271149).

