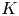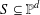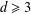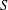Refine search
Actions for selected content:
8 results
On K-stability of blow-ups of weighted projective planes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-17
-
- Article
- Export citation
Delta-invariants of complete intersection log del Pezzo surfaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 1021-1036
- Print publication:
- June 2023
-
- Article
- Export citation
Super-rigid affine Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 17 October 2018, pp. 2462-2484
- Print publication:
- November 2018
-
- Article
- Export citation
Del Pezzo Surfaces in Weighted Projective Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 545-572
-
- Article
-
- You have access
- Export citation
RANK TWO STABLE ULRICH BUNDLES ON ANTICANONICALLY EMBEDDED SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 23 November 2016, pp. 22-37
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
A derived equivalence for a degree 6 del Pezzo surface over an arbitrary field
-
- Journal:
- Journal of K-Theory / Volume 8 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 20 January 2011, pp. 481-492
- Print publication:
- December 2011
-
- Article
- Export citation
Log canonical thresholds on Gorenstein canonical del Pezzo surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 187-219
-
- Article
-
- You have access
- Export citation
Smoothable del Pezzo surfaces with quotient singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 15 December 2009, pp. 169-192
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation