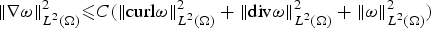Refine search
Actions for selected content:
31 results
Project 13: - Time Dependent Schrödinger Equation
-
- Book:
- A First Guide to Computational Modelling in Physics
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 81-85
-
- Chapter
- Export citation
Project 14: - Poisson’s Equation in 2D
-
- Book:
- A First Guide to Computational Modelling in Physics
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 86-91
-
- Chapter
- Export citation
Chapter 9 - Conclusion
-
- Book:
- Handbook of Augmented Reality Training Design Principles
- Published online:
- 18 May 2023
- Print publication:
- 01 June 2023, pp 128-136
-
- Chapter
- Export citation
12 - Dune Patterns in Sand Seas and Dune Fields
- from Part V - Sand Seas and Dune Fields
-
- Book:
- Geomorphology of Desert Dunes
- Published online:
- 03 March 2023
- Print publication:
- 23 March 2023, pp 226-239
-
- Chapter
- Export citation
10 - Lattice Models
-
- Book:
- Liquid Crystals and their Computer Simulations
- Published online:
- 21 July 2022
- Print publication:
- 28 July 2022, pp 401-433
-
- Chapter
- Export citation
8 - Monte Carlo Methods
-
- Book:
- Liquid Crystals and their Computer Simulations
- Published online:
- 21 July 2022
- Print publication:
- 28 July 2022, pp 359-378
-
- Chapter
- Export citation
22 - Glacial Isostatic Adjustment Models for Earthquake Triggering
- from Part VI - Modelling of Glacially Induced Faults and Stress
-
-
- Book:
- Glacially-Triggered Faulting
- Published online:
- 02 December 2021
- Print publication:
- 16 December 2021, pp 383-401
-
- Chapter
- Export citation
6 - Computational Fluid Dynamics for Steady and Unsteady Flows
-
- Book:
- Aircraft Aerodynamic Design with Computational Software
- Published online:
- 30 April 2021
- Print publication:
- 20 May 2021, pp 213-246
-
- Chapter
- Export citation
4 - Finite-Volume Schemes for the Euler Equations
-
- Book:
- Aircraft Aerodynamic Design with Computational Software
- Published online:
- 30 April 2021
- Print publication:
- 20 May 2021, pp 137-178
-
- Chapter
- Export citation
6 - Governing Equations and Boundary Conditions
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 146-179
-
- Chapter
- Export citation
VALIDATION CONCEPT FOR THE INVESTIGATION OF EFFECTS OF MODULAR PRODUCT FAMILIES
- Part of
-
- Journal:
- Proceedings of the Design Society: DESIGN Conference / Volume 1 / May 2020
- Published online by Cambridge University Press:
- 11 June 2020, pp. 2395-2404
-
- Article
-
- You have access
- Open access
- Export citation
4 - Boundary–Value Problems of Elasticity
- from Part I - Fundamentals of Solid Mechanics
-
- Book:
- Intermediate Solid Mechanics
- Published online:
- 16 December 2019
- Print publication:
- 09 January 2020, pp 81-102
-
- Chapter
- Export citation
4 - Electromagnetism: Fundamentals
-
- Book:
- Fast Techniques for Integrated Circuit Design
- Published online:
- 08 August 2019
- Print publication:
- 15 August 2019, pp 50-100
-
- Chapter
- Export citation
5 - Incompressible Solvers for Single-Phase Flow
- from Part II - Single-Phase Flow
-
- Book:
- An Introduction to Reservoir Simulation Using MATLAB/GNU Octave
- Published online:
- 22 July 2019
- Print publication:
- 08 August 2019, pp 143-173
-
- Chapter
-
- You have access
- Open access
- Export citation
4 - Mathematical Models for Single-Phase Flow
- from Part II - Single-Phase Flow
-
- Book:
- An Introduction to Reservoir Simulation Using MATLAB/GNU Octave
- Published online:
- 22 July 2019
- Print publication:
- 08 August 2019, pp 113-142
-
- Chapter
-
- You have access
- Open access
- Export citation
On the boundary conditions in estimating ∇ω by div ω and curl ω
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 739-760
- Print publication:
- June 2019
-
- Article
- Export citation
The perils of ethnographic analogy. Parallel logics in ethnoarchaeology and Victorian Bible customs books
-
- Journal:
- Archaeological Dialogues / Volume 25 / Issue 2 / December 2018
- Published online by Cambridge University Press:
- 06 November 2018, pp. 161-189
-
- Article
- Export citation
Natural Frequency and Buckling of Orthotropic Nanoplates Resting on Two-Parameter Elastic Foundations with Various Boundary Conditions
-
- Journal:
- Journal of Mechanics / Volume 30 / Issue 5 / October 2014
- Published online by Cambridge University Press:
- 12 August 2014, pp. 443-453
- Print publication:
- October 2014
-
- Article
- Export citation
24 - The Expertise Reversal Principle in Multimedia Learning
- from Part III - Advanced Principles of Multimedia Learning
-
-
- Book:
- The Cambridge Handbook of Multimedia Learning
- Published online:
- 05 August 2014
- Print publication:
- 28 July 2014, pp 576-597
-
- Chapter
- Export citation
Rectangular Lattice Boltzmann Equation for Gaseous Microscale Flow
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 306-330
- Print publication:
- April 2016
-
- Article
- Export citation