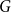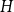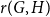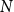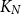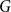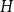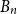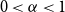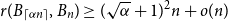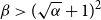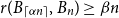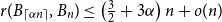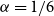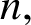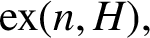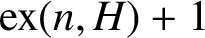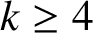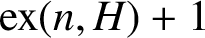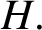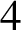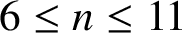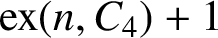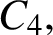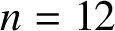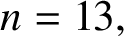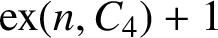Refine search
Actions for selected content:
11 results
Antarctic and Arctic science in the classroom and for society
- Part of
-
- Journal:
- Antarctic Science , First View
- Published online by Cambridge University Press:
- 28 October 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Libraries and the Academic Book
-
- Published online:
- 01 December 2024
- Print publication:
- 12 December 2024
-
- Element
- Export citation
Chapter 13 - The Printed Book in the Digital Age
-
-
- Book:
- The Cambridge Companion to Literature in a Digital Age
- Published online:
- 29 November 2024
- Print publication:
- 14 November 2024, pp 233-249
-
- Chapter
- Export citation
On a conjecture of Conlon, Fox, and Wigderson
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 432-445
-
- Article
- Export citation
Are popular books about diet and health written based on scientific evidence? A comparison of citations between the USA and Japan
-
- Journal:
- Public Health Nutrition / Volume 26 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 13 November 2023, pp. 2815-2825
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Practice of Piety Translated: The Dynamics of the International Circulation of a Devotional Book
-
- Journal:
- Church History / Volume 92 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 11 December 2023, pp. 559-584
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

William Faulkner and the Materials of Writing
-
- Published online:
- 24 May 2023
- Print publication:
- 05 January 2023
Gilayon and “Apocalypse”: Reconsidering an Early Jewish Concept and Genre
-
- Journal:
- Harvard Theological Review / Volume 116 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 190-227
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 6 - French
-
-
- Book:
- Literary Beginnings in the European Middle Ages
- Published online:
- 11 August 2022
- Print publication:
- 25 August 2022, pp 112-135
-
- Chapter
- Export citation

Is This a Book?
-
- Published online:
- 17 May 2022
- Print publication:
- 23 June 2022
-
- Element
- Export citation
ON A PROBLEM OF ERDŐS ABOUT GRAPHS WHOSE SIZE IS THE TURÁN NUMBER PLUS ONE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 177-187
- Print publication:
- April 2022
-
- Article
- Export citation