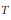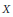Refine search
Actions for selected content:
4 results
On several dynamical properties of shifts acting on directed trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-30
-
- Article
- Export citation
Chaotic backward shift operator on Chebyshev polynomials
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 1025-1037
-
- Article
- Export citation
PSEUDOCONTINUATION AND CYCLICITY FOR RANDOM POWER SERIES
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 3 / July 2008
- Published online by Cambridge University Press:
- 27 February 2008, pp. 413-424
- Print publication:
- July 2008
-
- Article
- Export citation
The Commutant of an Abstract Backward Shift
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 1 / 01 March 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 21-24
- Print publication:
- 01 March 2000
-
- Article
-
- You have access
- Export citation