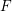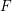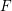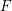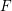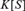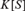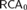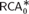Refine search
Actions for selected content:
6 results
2 - ACC for Log Canonical Thresholds for Complex Analytic Spaces
-
- Book:
- Higher Dimensional Algebraic Geometry
- Published online:
- 06 December 2024
- Print publication:
- 02 January 2025, pp 11-18
-
- Chapter
- Export citation
5 - Ideals
-
- Book:
- Algebraic Number Theory for Beginners
- Published online:
- 28 July 2022
- Print publication:
- 11 August 2022, pp 104-125
-
- Chapter
- Export citation
4 - Basic Real Algebraic Geometry in Rd
-
- Book:
- Polynomial Methods and Incidence Theory
- Published online:
- 17 March 2022
- Print publication:
- 24 March 2022, pp 51-65
-
- Chapter
- Export citation
Semigroups whose right ideals are finitely generated
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 01 October 2021, pp. 848-883
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ascending chain condition for
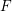 $F$-pure thresholds on a fixed strongly
$F$-pure thresholds on a fixed strongly 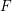 $F$-regular germ
$F$-regular germ
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 28 May 2019, pp. 1194-1223
- Print publication:
- June 2019
-
- Article
- Export citation
REVERSE MATHEMATICS, YOUNG DIAGRAMS, AND THE ASCENDING CHAIN CONDITION
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 19 June 2017, pp. 576-589
- Print publication:
- June 2017
-
- Article
- Export citation