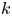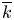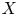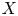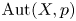Refine search
Actions for selected content:
53 results
ON THE SINGULARITIES OF QUOTIENTS BY 1-FOLIATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
20 - Energy conditions, singularity theorems, and wormholes
-
- Book:
- General Relativity
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025, pp 209-218
-
- Chapter
- Export citation
Chapter 4 - Abrupt Changes
- from Part II - Sudden Unexpected Changes
-
- Book:
- The Meaning of Paradoxes and Paradoxical Thinking
- Published online:
- 04 April 2025
- Print publication:
- 13 March 2025, pp 31-41
-
- Chapter
- Export citation
2 - ACC for Log Canonical Thresholds for Complex Analytic Spaces
-
- Book:
- Higher Dimensional Algebraic Geometry
- Published online:
- 06 December 2024
- Print publication:
- 02 January 2025, pp 11-18
-
- Chapter
- Export citation
On the gluing of germs of complex analytic spaces, Betti numbers, and their structure
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 582-597
- Print publication:
- June 2025
-
- Article
- Export citation
On the properness of the moduli space of stable surfaces over
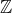 $\mathbb{Z}$[1/30]
$\mathbb{Z}$[1/30]
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTANCY OF THE HILBERT–SAMUEL FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 938-952
- Print publication:
- December 2024
-
- Article
- Export citation
Fields of moduli and the arithmetic of tame quotient singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 27 March 2024, pp. 982-1003
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kinematics of the Hybrid 6-Axis (H6A) manipulator
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Finite Ising Systems
-
- Book:
- A Student's Guide to the Ising Model
- Published online:
- 11 May 2023
- Print publication:
- 25 May 2023, pp 29-64
-
- Chapter
- Export citation
Time-optimal path following for non-redundant serial manipulators using an adaptive path-discretization
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On canonical Fano intrinsic quadrics
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 07 November 2022, pp. 288-309
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of singularities of cluster algebras of finite type: the case of trivial coefficients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 04 July 2022, pp. 170-204
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Global Spacetime Structure
-
- Published online:
- 13 November 2020
- Print publication:
- 03 December 2020
-
- Element
- Export citation
3 - Magnetically Structured Atmospheres
-
- Book:
- MHD Waves in the Solar Atmosphere
- Published online:
- 15 July 2019
- Print publication:
- 18 July 2019, pp 66-82
-
- Chapter
- Export citation
GEOMETRY OF INTEGRABLE LATTICE EQUATIONS AND THEIR REDUCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 17 May 2019, pp. 168-169
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Frame and direction mappings for surfaces in ℝ3
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 795-830
- Print publication:
- June 2019
-
- Article
- Export citation
The volume of singular Kähler–Einstein Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 1131-1158
- Print publication:
- June 2018
-
- Article
- Export citation