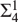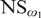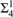Refine search
Actions for selected content:
31 results
Chapter 7 - Containment in Intuition
-
- Book:
- Kant and the Power of Perception
- Published online:
- 27 November 2025
- Print publication:
- 11 December 2025, pp 220-245
-
- Chapter
- Export citation
Saturation in random hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 07 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
6 - The Moist Atmosphere
- from Part II - Physics
-
- Book:
- The Science of Our Changing Climate
- Published online:
- 05 April 2024
- Print publication:
- 02 May 2024, pp 106-119
-
- Chapter
- Export citation

The Science of Our Changing Climate
-
- Published online:
- 05 April 2024
- Print publication:
- 02 May 2024
-
- Textbook
- Export citation
Anomalous hepatic drainage and platypnea-orthodeoxia in cyanotic children
-
- Journal:
- Cardiology in the Young / Volume 33 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 25 October 2023, pp. 2685-2689
-
- Article
- Export citation
Perfusion index in newborns with CHD without clinical signs of hypoperfusion and heart failure: comparison with healthy newborns
-
- Journal:
- Cardiology in the Young / Volume 33 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1092-1096
-
- Article
- Export citation
Integration questions in separably good characteristics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 890-932
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimization of Man Power Deployment for Covid-19 Screening in a Tertiary Care Hospital: A Study of Utility of Queuing Analysis
-
- Journal:
- Disaster Medicine and Public Health Preparedness / Volume 16 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 21 July 2021, pp. 2388-2392
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness and multiplicity of positive solutions for a diffusive predator–prey model in the heterogeneous environment
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 20 January 2020, pp. 3321-3348
- Print publication:
- December 2020
-
- Article
- Export citation
6 - NMR Polarization Measurement
-
- Book:
- The Physics of Polarized Targets
- Published online:
- 03 February 2020
- Print publication:
- 16 January 2020, pp 245-282
-
- Chapter
- Export citation
3 - Electron Paramagnetic Resonance and Relaxation
-
- Book:
- The Physics of Polarized Targets
- Published online:
- 03 February 2020
- Print publication:
- 16 January 2020, pp 98-154
-
- Chapter
- Export citation
5 - Tense Relationships: the Automotive Industry and Government
-
- Book:
- National Policy, Global Giants
- Published online:
- 14 December 2019
- Print publication:
- 02 January 2020, pp 126-149
-
- Chapter
- Export citation
8 - Mathematical Models for Multiphase Flow
- from Part III - Multiphase Flow
-
- Book:
- An Introduction to Reservoir Simulation Using MATLAB/GNU Octave
- Published online:
- 22 July 2019
- Print publication:
- 08 August 2019, pp 231-271
-
- Chapter
-
- You have access
- Open access
- Export citation
A
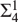 ${\rm{\Sigma }}_4^1 $ WELLORDER OF THE REALS WITH
${\rm{\Sigma }}_4^1 $ WELLORDER OF THE REALS WITH 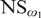 ${\rm{NS}}_{\omega _1 } $ SATURATED
${\rm{NS}}_{\omega _1 } $ SATURATED
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 16 July 2019, pp. 1466-1483
- Print publication:
- December 2019
-
- Article
- Export citation
Nonlinear DOB-based explicit NMPC for station-keeping of a multi-vectored propeller airship with thrust saturation
-
- Journal:
- The Aeronautical Journal / Volume 122 / Issue 1257 / November 2018
- Published online by Cambridge University Press:
- 15 November 2018, pp. 1753-1774
-
- Article
- Export citation
Theoretical aspect of enhancement and saturation in emission from laser produced plasma
-
- Journal:
- Laser and Particle Beams / Volume 30 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 25 September 2012, pp. 621-631
-
- Article
- Export citation
Statistics of joint spacing in rock layers
-
- Journal:
- Geological Magazine / Volume 149 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 03 May 2012, pp. 1065-1076
-
- Article
- Export citation
10 years of 12.2 GHz methanol maser VLBI observations towards NGC 7538 IRS1 N: proper motions and maser saturation
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 8 / Issue S287 / January 2012
- Published online by Cambridge University Press:
- 24 July 2012, pp. 186-187
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Interactions between species and the structure of helminth communities
-
- Journal:
- Parasitology / Volume 122 / Issue S1 / March 2001
- Published online by Cambridge University Press:
- 24 October 2011, pp. S3-S11
-
- Article
- Export citation