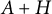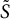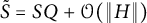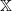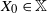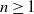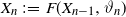Refine search
Actions for selected content:
39 results
LOCAL COHOMOLOGY UNDER SMALL PERTURBATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 183-200
- Print publication:
- June 2025
-
- Article
- Export citation
Sensitivity Analysis of Structural Equation Models
-
- Journal:
- Psychometrika / Volume 61 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 January 2025, pp. 93-108
-
- Article
- Export citation
Non-integrability of the restricted three-body problem
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 3012-3040
- Print publication:
- October 2024
-
- Article
- Export citation
Block perturbation of symplectic matrices in Williamson’s theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 201-214
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Robustness of iterated function systems of Lipschitz maps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 921-944
- Print publication:
- September 2023
-
- Article
- Export citation
14 - Time-Dependent Perturbation Theory
-
- Book:
- Quantum Mechanics
- Published online:
- 11 February 2023
- Print publication:
- 15 September 2022, pp 445-468
-
- Chapter
- Export citation
10 - Perturbation Theory
-
- Book:
- Quantum Mechanics
- Published online:
- 11 February 2023
- Print publication:
- 15 September 2022, pp 312-354
-
- Chapter
- Export citation
11 - Hyperfine Structure and the Addition of Angular Momenta
-
- Book:
- Quantum Mechanics
- Published online:
- 11 February 2023
- Print publication:
- 15 September 2022, pp 355-381
-
- Chapter
- Export citation
12 - Perturbation of Hydrogen
-
- Book:
- Quantum Mechanics
- Published online:
- 11 February 2023
- Print publication:
- 15 September 2022, pp 382-409
-
- Chapter
- Export citation
Chapter 12 - Psychological Science as a Complex Dynamic System
-
- Book:
- Toward a Process Approach in Psychology
- Published online:
- 14 July 2022
- Print publication:
- 28 July 2022, pp 266-291
-
- Chapter
- Export citation
Chapter 8 - (Compl)explanation and King Alfonso’s Lament
-
- Book:
- Toward a Process Approach in Psychology
- Published online:
- 14 July 2022
- Print publication:
- 28 July 2022, pp 160-188
-
- Chapter
- Export citation
The fragmentation equation with size diffusion: Well posedness and long-term behaviour
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 16 December 2021, pp. 1083-1116
-
- Article
- Export citation
21 - WEP as an extension property
-
- Book:
- Tensor Products of <I>C</I>*-Algebras and Operator Spaces
- Published online:
- 10 February 2020
- Print publication:
- 27 February 2020, pp 358-365
-
- Chapter
- Export citation
Towards the quantitative characterisation of piglets’ robustness to weaning: a modelling approach
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IMPLEMENTING STOCHASTIC VOLATILITY IN DSGE MODELS: A COMMENT
-
- Journal:
- Macroeconomic Dynamics / Volume 24 / Issue 4 / June 2020
- Published online by Cambridge University Press:
- 29 November 2018, pp. 935-950
-
- Article
- Export citation
MEASURING DEPENDENCE IN METRIC ABSTRACT ELEMENTARY CLASSES WITH PERTURBATIONS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1199-1228
- Print publication:
- December 2017
-
- Article
- Export citation
Spatio-temporal analysis of benthic polychaete community structure in the north-western coast of Baja California, Mexico
-
- Journal:
- Journal of the Marine Biological Association of the United Kingdom / Volume 97 / Issue 5 / August 2017
- Published online by Cambridge University Press:
- 10 August 2017, pp. 993-1005
-
- Article
- Export citation
Advances in the Neuroscience of Intelligence: from Brain Connectivity to Brain Perturbation
-
- Journal:
- The Spanish Journal of Psychology / Volume 19 / 2016
- Published online by Cambridge University Press:
- 06 December 2016, E94
-
- Article
- Export citation