Article contents
The fragmentation equation with size diffusion: Well posedness and long-term behaviour
Published online by Cambridge University Press: 16 December 2021
Abstract
The dynamics of the fragmentation equation with size diffusion is investigated when the size ranges in 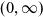 $(0,\infty)$. The associated linear operator involves three terms and can be seen as a nonlocal perturbation of a Schrödinger operator. A Miyadera perturbation argument is used to prove that it is the generator of a positive, analytic semigroup on a weighted
$(0,\infty)$. The associated linear operator involves three terms and can be seen as a nonlocal perturbation of a Schrödinger operator. A Miyadera perturbation argument is used to prove that it is the generator of a positive, analytic semigroup on a weighted 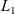 $L_1$-space. Moreover, if the overall fragmentation rate does not vanish at infinity, then there is a unique stationary solution with given mass. Assuming further that the overall fragmentation rate diverges to infinity for large sizes implies the immediate compactness of the semigroup and that it eventually stabilizes at an exponential rate to a one-dimensional projection carrying the information of the mass of the initial value.
$L_1$-space. Moreover, if the overall fragmentation rate does not vanish at infinity, then there is a unique stationary solution with given mass. Assuming further that the overall fragmentation rate diverges to infinity for large sizes implies the immediate compactness of the semigroup and that it eventually stabilizes at an exponential rate to a one-dimensional projection carrying the information of the mass of the initial value.
Information
- Type
- Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 2
- Cited by


