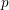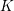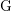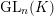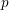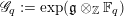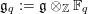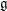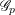Refine search
Actions for selected content:
2 results
Kirillov’s orbit method and polynomiality of the faithful dimension of
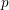 $p$-groups
$p$-groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 11 July 2019, pp. 1618-1654
- Print publication:
- August 2019
-
- Article
- Export citation
SUPERORBITS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 20 July 2016, pp. 1065-1120
- Print publication:
- November 2018
-
- Article
- Export citation