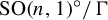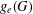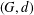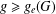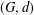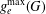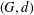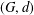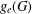Refine search
Actions for selected content:
5 results
Effective equidistribution of horospherical flows in infinite volume rank-one homogeneous spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 09 August 2022, pp. 2780-2840
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Packable hyperbolic surfaces with symmetries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 11 February 2022, pp. 103-113
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EMBEDDING OF METRIC GRAPHS ON HYPERBOLIC SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 508-520
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
SYSTOLIC FILLINGS OF SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 28 August 2018, pp. 502-511
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Isoperimetric Inequalities on Surfaces of Constant Curvature
-
- Journal:
- Canadian Journal of Mathematics / Volume 49 / Issue 6 / 01 December 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1162-1187
- Print publication:
- 01 December 1997
-
- Article
-
- You have access
- Export citation