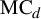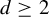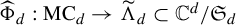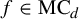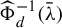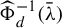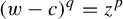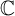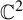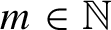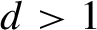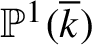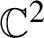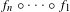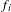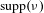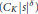Refine search
Actions for selected content:
15 results
Entire maps with rational preperiodic points and multipliers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 15 January 2025, pp. 2636-2658
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transcendental Julia sets of minimal Hausdorff dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2341-2413
- Print publication:
- August 2025
-
- Article
- Export citation
The moduli space of polynomial maps and their fixed-point multipliers: II. Improvement to the algorithm and monic centered polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 3777-3795
- Print publication:
- November 2023
-
- Article
- Export citation
Introduction
-
- Book:
- Artificial Economics
- Published online:
- 28 October 2021
- Print publication:
- 04 November 2021, pp 1-4
-
- Chapter
- Export citation
Dynamics of hyperbolic correspondences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2661-2692
- Print publication:
- August 2022
-
- Article
- Export citation
Lee-Yang zeros of the antiferromagnetic Ising model
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2172-2206
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Value distribution of derivatives in polynomial dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 05 January 2021, pp. 3780-3806
- Print publication:
- December 2021
-
- Article
- Export citation
Knobbly but nice
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 08 May 2020, pp. 2016-2022
- Print publication:
- July 2021
-
- Article
- Export citation
14 - Foundations of Ecological-Economic Modelling
- from Part IV - Ecological-Economic Modelling
-
- Book:
- Ecological-Economic Modelling for Biodiversity Conservation
- Published online:
- 29 February 2020
- Print publication:
- 26 March 2020, pp 195-205
-
- Chapter
- Export citation
Random local complex dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 2156-2182
- Print publication:
- August 2020
-
- Article
- Export citation
Modeling the effect of farmers' decisions on the population dynamics of winter wild oat in an agricultural landscape
-
- Journal:
- Weed Science / Volume 49 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 20 January 2017, pp. 414-422
-
- Article
- Export citation
MONETARY POLICY AND DEBT DEFLATION: SOME COMPUTATIONAL EXPERIMENTS
-
- Journal:
- Macroeconomic Dynamics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 April 2016, pp. 214-242
-
- Article
- Export citation
DISCRETE CHOICE AND COMPLEX DYNAMICS IN DETERMINISTIC OPTIMIZATION PROBLEMS
-
- Journal:
- Macroeconomic Dynamics / Volume 16 / Issue S1 / April 2012
- Published online by Cambridge University Press:
- 13 February 2012, pp. 52-69
-
- Article
- Export citation
Growth and Zeros of the Zeta Function for Hyperbolic Rational Maps
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 2 / 01 April 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 311-331
- Print publication:
- 01 April 2007
-
- Article
-
- You have access
- Export citation
DYNAMICS OF NATURAL RATES OF GROWTH AND EMPLOYMENT
-
- Journal:
- Macroeconomic Dynamics / Volume 2 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 September 1998, pp. 345-368
-
- Article
- Export citation