Published online by Cambridge University Press: 20 November 2018
This paper describes new results on the growth and zeros of the Ruelle zeta function for the Julia set of a hyperbolic rational map. It is shown that the zeta function is bounded by exp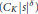 $({{C}_{k}}{{\left| s \right|}^{\delta }})$ in strips
$({{C}_{k}}{{\left| s \right|}^{\delta }})$ in strips 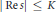 $|\,\text{Re}\,s\,|\,\le \,K$, where
$|\,\text{Re}\,s\,|\,\le \,K$, where  $\delta$ is the dimension of the Julia set. This leads to bounds on the number of zeros in strips (interpreted as the Pollicott–Ruelle resonances of this dynamical system). An upper bound on the number of zeros in polynomial regions
$\delta$ is the dimension of the Julia set. This leads to bounds on the number of zeros in strips (interpreted as the Pollicott–Ruelle resonances of this dynamical system). An upper bound on the number of zeros in polynomial regions 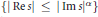 $\left\{ \left| \,\operatorname{Re}s \right|\,\le \,{{\left| \,\operatorname{Im}s \right|}^{\alpha }} \right\}$ is given, followed by weaker lower bound estimates in strips
$\left\{ \left| \,\operatorname{Re}s \right|\,\le \,{{\left| \,\operatorname{Im}s \right|}^{\alpha }} \right\}$ is given, followed by weaker lower bound estimates in strips 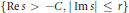 $\{\text{Re}\,s\,>\,-C,\,|\,\text{IM}\,s|\,\le \,r\}$, and logarithmic neighbourhoods
$\{\text{Re}\,s\,>\,-C,\,|\,\text{IM}\,s|\,\le \,r\}$, and logarithmic neighbourhoods 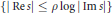 $\{|\text{Re}s|\le {{}_{\rho }}\log |\operatorname{Im}s|\}$. Recent numerical work of Strain-Zworski suggests the upper bounds in strips are optimal.
$\{|\text{Re}s|\le {{}_{\rho }}\log |\operatorname{Im}s|\}$. Recent numerical work of Strain-Zworski suggests the upper bounds in strips are optimal.