Refine search
Actions for selected content:
16 results
A Cesàro-like operator from a class of analytic function spaces to analytic Besov spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1210-1222
- Print publication:
- December 2025
-
- Article
- Export citation
Hilbert type operators acting from the Bloch space into Bergman spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 205-225
-
- Article
- Export citation
ON THE HARMONIC ZYGMUND SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 11 March 2020, pp. 466-476
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
POWERS OF COMPOSITION OPERATORS: ASYMPTOTIC BEHAVIOUR ON BERGMAN, DIRICHLET AND BLOCH SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 27 November 2019, pp. 289-320
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
SPECTRA OF LINEAR FRACTIONAL COMPOSITION OPERATORS ON THE GROWTH SPACE AND BLOCH SPACE OF THE UPPER HALF-PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 199-214
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Inclusion Relations for New Function Spaces on Riemann Surfaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 466-476
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
Linear Combinations of Composition Operators on the Bloch Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 4 / 01 August 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 862-877
- Print publication:
- 01 August 2011
-
- Article
-
- You have access
- Export citation
Multiplicative Isometries and Isometric Zero-Divisors
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 5 / 01 October 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-974
- Print publication:
- 01 October 2010
-
- Article
-
- You have access
- Export citation
THE ESSENTIAL NORM OF A WEIGHTED COMPOSITION OPERATOR FROM THE BLOCH SPACE TO H∞
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 05 May 2009, pp. 487-497
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
DIFFERENCES OF COMPOSITION OPERATORS ON THE BLOCH SPACE IN THE POLYDISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 465-471
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
ISOMETRIES AND SPECTRA OF MULTIPLICATION OPERATORS ON THE BLOCH SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 147-160
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
WEIGHTED LIPSCHITZ CONTINUITY AND HARMONIC BLOCH AND BESOV SPACES IN THE REAL UNIT BALL
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 48 / Issue 3 / October 2005
- Published online by Cambridge University Press:
- 15 September 2005, pp. 743-755
-
- Article
-
- You have access
- Export citation
The Essential Norm of a Bloch-to-
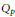 ${{Q}_{p}}$ Composition Operator
${{Q}_{p}}$ Composition Operator
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 1 / 01 March 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 49-59
- Print publication:
- 01 March 2004
-
- Article
-
- You have access
- Export citation
Composition operators on Qp spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 161-188
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
Coefficient Multipliers of Bergman Spaces A p , II
-
- Journal:
- Canadian Mathematical Bulletin / Volume 40 / Issue 4 / 01 December 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 475-487
- Print publication:
- 01 December 1997
-
- Article
-
- You have access
- Export citation
Note on the Space Bmoa
-
- Journal:
- Canadian Mathematical Bulletin / Volume 35 / Issue 1 / 01 March 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 40-45
- Print publication:
- 01 March 1992
-
- Article
-
- You have access
- Export citation


























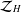

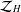
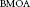
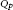
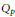
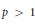
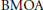
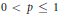
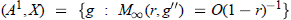 , where
, where 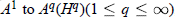 , we also give the multipliers from
, we also give the multipliers from 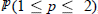 ,
, 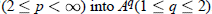 .
.

