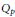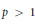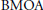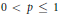Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rättyä, Jouni
2007.
The essential norm of a composition operator mapping into the Qs-space.
Journal of Mathematical Analysis and Applications,
Vol. 333,
Issue. 2,
p.
787.
Laitila, Jussi
2009.
Weighted Composition Operators on BMOA.
Computational Methods and Function Theory,
Vol. 9,
Issue. 1,
p.
27.
Pau, Jordi
2009.
Composition Operators between Bloch-Type Spaces and Möbius Invariant $\Qk$ Spaces.
Rocky Mountain Journal of Mathematics,
Vol. 39,
Issue. 6,
Wang, Maofa
and
Wu, Huanqin
2011.
Norms and essential norms of composition operators from H
∞
to general weighted Bloch spaces in the polydisk.
Journal of Inequalities and Applications,
Vol. 2011,
Issue. 1,
Ueki, Sei-ichiro
2012.
Weighted composition operators acting between the Np-space and the weighted-type space Hα∞.
Indagationes Mathematicae,
Vol. 23,
Issue. 3,
p.
243.
Abakumov, Evgeny
and
Doubtsov, Evgueni
2012.
Reverse estimates in growth spaces.
Mathematische Zeitschrift,
Vol. 271,
Issue. 1-2,
p.
399.
Yu, Yanyan
and
Liu, Yongmin
2012.
The Essential Norm of a Generalized Composition Operator Between Bloch-Type Spaces and Q K Type Spaces.
Complex Analysis and Operator Theory,
Vol. 6,
Issue. 6,
p.
1231.
Galindo, Pablo
Laitila, Jussi
and
Lindström, Mikael
2013.
Essential norm estimates for composition operators on BMOA.
Journal of Functional Analysis,
Vol. 265,
Issue. 4,
p.
629.
Laitila, Jussi
Nieminen, Pekka J.
Saksman, Eero
and
Tylli, Hans-Olav
2013.
Compact and Weakly Compact Composition Operators on BMOA.
Complex Analysis and Operator Theory,
Vol. 7,
Issue. 1,
p.
163.
Makhmutov, S. A.
and
Makhmutova, M. S.
2019.
Metric Spaces of Bounded Analytical Functions.
Journal of Mathematical Sciences,
Vol. 241,
Issue. 6,
p.
750.
Liu, Xiaoman
Liu, Yongmin
Xia, Lina
and
Yu, Yanyan
2020.
The essential norm of the integral type operators.
Banach Journal of Mathematical Analysis,
Vol. 14,
Issue. 1,
p.
181.
Tang, Shuan
and
Wu, Pengcheng
2020.
Composition Operator, Boundedness, Compactness, Hyperbolic Bloch-Type Space βμ∗, Hyperbolic-Type Space.
Journal of Function Spaces,
Vol. 2020,
Issue. ,
p.
1.
Göğüş, Nihat Gökhan
2022.
Projective limits of Dirichlet spaces and embeddings of Bloch-type spaces.
Annals of Functional Analysis,
Vol. 13,
Issue. 3,
Hai Khoi, Le
and
Mashreghi, Javad
2023.
Theory of Np Spaces.
p.
55.
Göğüş, Nihat Gökhan
2024.
Growth Spaces on Circular Domains Taking Values in a Banach Lattice, Embeddings and Composition Operators.
Mathematics,
Vol. 12,
Issue. 16,
p.
2554.