Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Buckley, Stephen M.
Ramanujan, M. S.
and
Vukotić, Dragan
1999.
Bounded and compact multipliers between Bergman and Hardy spaces.
Integral Equations and Operator Theory,
Vol. 35,
Issue. 1,
p.
1.
Lou, Zeng Jian
Guo, Ji Dong
and
Song, Dao Jin
2003.
Multipliers and Cyclic Vectors in Bloch Type Spaces.
Acta Mathematica Sinica, English Series,
Vol. 19,
Issue. 1,
p.
79.
Lou, Zengjian
and
Wulan, Hasi
2003.
Characterisations of Bloch functions in the unit ball of ℂn, I.
Bulletin of the Australian Mathematical Society,
Vol. 68,
Issue. 2,
p.
205.
Naik, Sunanda
and
Rajbangshi, Karabi
2014.
Multipliers on H(p, q, α) spaces.
Arabian Journal of Mathematics,
Vol. 3,
Issue. 3,
p.
349.
Jevtić, Miroljub
Vukotić, Dragan
and
Arsenović, Miloš
2016.
Taylor Coefficients and Coefficient Multipliers of Hardy and Bergman-Type Spaces.
Vol. 2,
Issue. ,
p.
247.
Jevtić, Miroljub
Vukotić, Dragan
and
Arsenović, Miloš
2016.
Taylor Coefficients and Coefficient Multipliers of Hardy and Bergman-Type Spaces.
Vol. 2,
Issue. ,
p.
237.
Naik, S.
and
Rajbangshi, K.
2017.
Coefficient multipliers on mixed-norm spaces
$$H(p,q,\varphi )$$
H
(
p
,
q
,
φ
)
.
The Journal of Analysis,
Vol. 25,
Issue. 1,
p.
29.


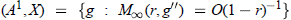 , where
, where 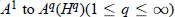 , we also give the multipliers from
, we also give the multipliers from 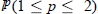 ,
, 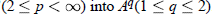 .
.