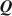Refine search
Actions for selected content:
90 results
The unpredictable role of language distance in bilingual cognition: A systematic review from brain to behavior
-
- Journal:
- Bilingualism: Language and Cognition , First View
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A unified Bayesian framework for mortality model selection
-
- Journal:
- Annals of Actuarial Science / Volume 19 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 17 October 2025, pp. 462-481
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - Estimation for Structural Models
- from Part II - Intermediate Concepts
-
- Book:
- Statistics for Chemical Engineers
- Published online:
- 12 December 2025
- Print publication:
- 25 September 2025, pp 210-286
-
- Chapter
- Export citation
Humility and Complexity
-
- Journal:
- Canadian Journal of Philosophy , FirstView
- Published online by Cambridge University Press:
- 20 August 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Placebo and nocebo phenomena in schizophrenia spectrum disorders: a narrative review on current knowledge and potential future directions
-
- Journal:
- Psychological Medicine / Volume 55 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e199
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - Predictive Coding Models of Attention
-
- Book:
- Neuroscience of Attention
- Published online:
- 02 May 2025
- Print publication:
- 22 May 2025, pp 315-348
-
- Chapter
- Export citation
Meta-analysis with Jeffreys priors: Empirical frequentist properties
-
- Journal:
- Research Synthesis Methods / Volume 16 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 87-122
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - Methods for Estimating Discrete-Time Stochastic Volatility Models
- from Part III - Bayesian Estimation and Inferences
-
- Book:
- Financial Econometrics
- Published online:
- 20 February 2025
- Print publication:
- 27 February 2025, pp 271-305
-
- Chapter
- Export citation
Estimating the Cognitive Diagnosis Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\varvec{Q}$$\end{document}
 Matrix with Expert Knowledge: Application to the Fraction-Subtraction Dataset
Matrix with Expert Knowledge: Application to the Fraction-Subtraction Dataset
-
- Journal:
- Psychometrika / Volume 84 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 01 January 2025, pp. 333-357
-
- Article
- Export citation
Gibbs Samplers for Logistic Item Response Models via the Pólya–Gamma Distribution: A Computationally Efficient Data-Augmentation Strategy
-
- Journal:
- Psychometrika / Volume 84 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 01 January 2025, pp. 358-374
-
- Article
- Export citation
Revisiting the 4-Parameter Item Response Model: Bayesian Estimation and Application
-
- Journal:
- Psychometrika / Volume 81 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 01 January 2025, pp. 1142-1163
-
- Article
- Export citation
Bayesian Mixture Model of Extended Redundancy Analysis
-
- Journal:
- Psychometrika / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 01 January 2025, pp. 946-966
-
- Article
- Export citation
The Reliability Factor: Modeling Individual Reliability with Multiple Items from a Single Assessment
-
- Journal:
- Psychometrika / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 01 January 2025, pp. 1318-1342
-
- Article
- Export citation
A Hierarchical Ornstein–Uhlenbeck Model for Continuous Repeated Measurement Data
-
- Journal:
- Psychometrika / Volume 74 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 January 2025, pp. 395-418
-
- Article
- Export citation
Inferring the Number of Attributes for the Exploratory DINA Model
-
- Journal:
- Psychometrika / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 January 2025, pp. 30-64
-
- Article
- Export citation
A Latent Space Network Model for Social Influence
-
- Journal:
- Psychometrika / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 01 January 2025, pp. 251-274
-
- Article
- Export citation
Bayesian Hierarchical Classes Analysis
-
- Journal:
- Psychometrika / Volume 73 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 January 2025, pp. 39-64
-
- Article
- Export citation
Detecting Multiple Random Changepoints in Bayesian Piecewise Growth Mixture Models
-
- Journal:
- Psychometrika / Volume 83 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 01 January 2025, pp. 733-750
-
- Article
- Export citation
Forecasting Intra-individual Changes of Affective States Taking into Account Inter-individual Differences Using Intensive Longitudinal Data from a University Student Dropout Study in Math
-
- Journal:
- Psychometrika / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 01 January 2025, pp. 533-558
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Comparing Bayesian Variable Selection to Lasso Approaches for Applications in Psychology
-
- Journal:
- Psychometrika / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 01 January 2025, pp. 1032-1055
-
- Article
-
- You have access
- Open access
- HTML
- Export citation