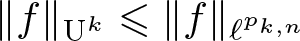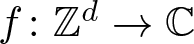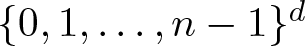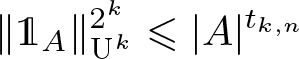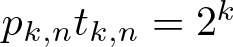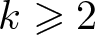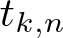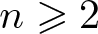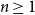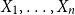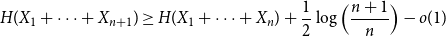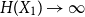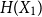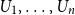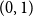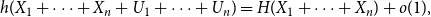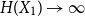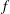Refine search
Actions for selected content:
33 results
Non-parametric estimation of the generalized past entropy function under α-mixing sample
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 05 November 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Introducing and applying varinaccuracy: a measure for doubly truncated random variables in reliability analysis
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 05 September 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative entropy bounds for sampling with and without replacement
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1578-1593
- Print publication:
- December 2025
-
- Article
- Export citation
Sharp estimates for Gowers norms on discrete cubes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1-27
-
- Article
- Export citation
Extropy-based dynamic cumulative residual inaccuracy measure: properties and applications
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 4 / October 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 461-485
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some generalized information and divergence generating functions: properties, estimation, validation, and applications
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 3 / July 2025
- Published online by Cambridge University Press:
- 25 February 2025, pp. 397-430
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal experimental design: Formulations and computations
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 715-840
-
- Article
-
- You have access
- Open access
- Export citation
Quantile-based information generating functions and their properties and uses
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 733-751
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence rate of entropy-regularized multi-marginal optimal transport costs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1072-1092
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Ziv–Merhav theorem beyond Markovianity I
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 891-915
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximate discrete entropy monotonicity for log-concave sums
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 196-209
-
- Article
- Export citation
The unified extropy and its versions in classical and Dempster–Shafer theories
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 685-696
- Print publication:
- June 2024
-
- Article
- Export citation
Costa’s concavity inequality for dependent variables based on the multivariate Gaussian copula
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 12 April 2023, pp. 1136-1156
- Print publication:
- December 2023
-
- Article
- Export citation
A new lifetime distribution by maximizing entropy: properties and applications
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 February 2023, pp. 189-206
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Varentropy of doubly truncated random variable
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 852-871
-
- Article
- Export citation
On reconsidering entropies and divergences and their cumulative counterparts: Csiszár's, DPD's and Fisher's type cumulative and survival measures
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 21 February 2022, pp. 294-321
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Concentration functions and entropy bounds for discrete log-concave distributions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 54-72
-
- Article
- Export citation
PROBABILISTIC STABILITY, AGM REVISION OPERATORS AND MAXIMUM ENTROPY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 October 2020, pp. 553-590
- Print publication:
- September 2022
-
- Article
- Export citation
Orlicz Addition for Measures and an Optimization Problem for the
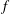 $f$-divergence
$f$-divergence
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 16 July 2019, pp. 455-479
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
CONVEXITY OF PARAMETER EXTENSIONS OF SOME RELATIVE OPERATOR ENTROPIES WITH A PERSPECTIVE APPROACH
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 737-744
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation