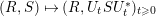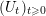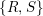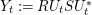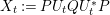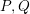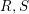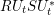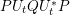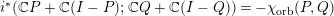1 Introduction
Let 
$(\mathscr{A},\unicode[STIX]{x1D70F})$ be a 
$W^{\ast }$-probability space and let 
$(U_{t})_{t\geqslant 0}$ be a free unitary Brownian motion in 
$(\mathscr{A},\unicode[STIX]{x1D70F})$ with 
$U_{0}=\mathbf{1}$. For a given pair of orthogonal projections 
$\{P,Q\}$ in 
$\mathscr{A}$ that are freely independent from 
$(U_{t})_{t\geqslant 0}$, the so-called liberation process 
$(P,Q)\mapsto (P,U_{t}QU_{t}^{\ast })$ was introduced in [Reference Voiculescu19] in relation with the free entropy and the free Fisher information. In this paper, we are interested in the following variant of the liberation process: 
$(R,S)\mapsto (R,U_{t}SU_{t}^{\ast })$ where 
$\{R,S\}$ are the symmetries associated with 
$\{P,Q\}$, namely 
$R=2P-\mathbf{1},S=2Q-\mathbf{1}$. It is known, as a consequence of the asymptotic freeness of 
$P$ and 
$U_{t}QU_{t}^{\ast }$, that the pair 
$(R,U_{t}SU_{t}^{\ast })$ tends, as 
$t\rightarrow \infty$, to 
$(R,USU^{\ast })$ where 
$U$ is a Haar unitary free from 
$\{R,S\}$ and hence 
$R,USU^{\ast }$ are free (see [Reference Nica and Speicher17]). The connection between the two liberation processes can be understood by studying the relationship between their actions on the operators 
$X_{t}:=PU_{t}QU_{t}^{\ast }P$ and 
$Y_{t}:=RU_{t}SU_{t}^{\ast }$. This study is actually motivated by the important problem of proving the conjectured identity 
$i^{\ast }=-\unicode[STIX]{x1D712}_{\text{orb}}$ for two projections with arbitrary ranks. Here, 
$i^{\ast }$ is the free mutual information introduced by Voiculescu (see [Reference Voiculescu19]) and 
$\unicode[STIX]{x1D712}_{\text{orb}}$ is the orbital free entropy due to Hiai, Miyamoto and Ueda (see [Reference Hiai, Miyamoto and Ueda12, Reference Ueda18]). A heuristic argument provided in [Reference Hiai and Ueda14, Section 3.2] supports this conjecture which was proved in [Reference Collins and Kemp4] in the special case 
$\unicode[STIX]{x1D70F}(P)=\unicode[STIX]{x1D70F}(Q)=1/2$, then subsequently in [Reference Izumi and Ueda15]. In this last paper, the authors used a subordination relation to give more partial results for arbitrary ranks.
Here, we improve the results in [Reference Izumi and Ueda15] by providing a detailed explicit study of the unique subordinate family. To this end, we use stochastic calculus in order to derive a PDE for the Herglotz transform 
$H(t,z)$ of the spectral measure, says 
$\unicode[STIX]{x1D708}_{t}$, of 
$Y_{t}$. It turns out that this is exactly the PDE governing the flow of an analytic function transform of the spectral measure, says 
$\unicode[STIX]{x1D707}_{t}$, of 
$X_{t}$ (see Remark 3.6 below). This allows us to develop a theory of subordination for the process 
$Y_{t}$ akin to [Reference Izumi and Ueda15]. In particular, we obtain an explicit computation of the subordinate function (which is a one-to-one map in the unit disc) and use it to show that its inverse extends continuously to the unit circle. As an application of our results, we prove under mild assumptions the identity 
$i^{\ast }=-\unicode[STIX]{x1D712}_{\text{orb}}$ for arbitrary ranks 
$\unicode[STIX]{x1D70F}(P)$ and 
$\unicode[STIX]{x1D70F}(Q)$.
2 Analysis of the spectral measure of 
$Y_{t}$
2.1 Sequence of moments
Let 
$R,S\in \mathscr{A}$ be two orthogonal symmetries and 
$U_{t},t\in [0,\infty )$ a free unitary Brownian motion freely independent from 
$\{R,S\}$. Our goal here is to derive a system of ODEs satisfied by the sequence of moments of 
$\unicode[STIX]{x1D708}_{t}$ via free stochastic calculus.
Proposition 2.1. Let 
$f_{n}(t):=\unicode[STIX]{x1D70F}([RU_{t}SU_{t}^{\ast }]^{n})\;n\geqslant 1,t\geqslant 0$, then
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}f_{1}=-f_{1}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}, & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x2202}_{t}f_{n}=-nf_{n}-n\displaystyle \mathop{\sum }_{k=1}^{n-1}f_{k}f_{n-k}+\left\{\begin{array}{@{}ll@{}}\displaystyle n^{2}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\quad & \text{if }n\text{ is odd}\\ \displaystyle n^{2}\frac{\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2}}{2}\quad & \text{if }n\text{ is even,}\end{array}\right.\quad n\geqslant 2 & \displaystyle \nonumber\end{eqnarray}$$ where 
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70F}(R)$ and 
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70F}(S)$.
Proof. Let 
$A_{t}=RU_{t}SU_{t}^{\ast }$, then using Ito’s formula, we have
$$\begin{eqnarray}d[A_{t}^{n}]=\mathop{\sum }_{k=1}^{n}A_{t}^{k-1}dA_{t}\,A_{t}^{n-k}+\mathop{\sum }_{1\leqslant j<k\leqslant n}A_{t}^{j-1}dA_{t}\,A_{t}^{k-j-1}dA_{t}\,A_{t}^{n-k}.\end{eqnarray}$$Taking the trace in both sides and use the trace property, we get
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(d[A_{t}^{n}])=\mathop{\sum }_{k=1}^{n}\unicode[STIX]{x1D70F}(A_{t}^{n-1}dA_{t})+\mathop{\sum }_{1\leqslant j<k\leqslant n}\unicode[STIX]{x1D70F}(A_{t}^{n-(k-j)-1}dA_{t}\,A_{t}^{k-j-1}dA_{t}).\end{eqnarray}$$ The first summands do not depend on the summation variable 
$k$, while the second summands depend on the summation variable 
$j,k$ only through their difference 
$k-j$. Then reindexing by 
$l=k-j$, we get
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(d[A_{t}^{n}])=n\unicode[STIX]{x1D70F}(A_{t}^{n-1}dA_{t})+\mathop{\sum }_{l=1}^{n-1}\mathop{\sum }_{1\leqslant j<k\leqslant n,~k-j=l}\unicode[STIX]{x1D70F}(A_{t}^{n-l-1}dA_{t}\,A_{t}^{l-1}dA_{t}).\end{eqnarray}$$ Since the number of pairs 
$(j,k)$ such that 
$k-j=l$ for fixed 
$l$ is equal to 
$n-l$, then the second summation becomes
$$\begin{eqnarray}\mathop{\sum }_{l=1}^{n-1}(n-l)\unicode[STIX]{x1D70F}(A_{t}^{n-l-1}dA_{t}\,A_{t}^{l-1}dA_{t}).\end{eqnarray}$$ This sum rewrites, after reindexing 
$k=n-l$, as
$$\begin{eqnarray}\mathop{\sum }_{k=1}^{n-1}k\unicode[STIX]{x1D70F}(A_{t}^{k-1}dA_{t}\,A_{t}^{n-k-1}dA_{t}).\end{eqnarray}$$Using the trace property and adding the summations (2.1) and (2.2), we get
$$\begin{eqnarray}\mathop{\sum }_{k=1}^{n-1}(n-k+k)\unicode[STIX]{x1D70F}(A_{t}^{n-k-1}dA_{t}\,A_{t}^{k-1}dA_{t})=n\mathop{\sum }_{k=1}^{n-1}\unicode[STIX]{x1D70F}(A_{t}^{n-k-1}dA_{t}\,A_{t}^{k-1}dA_{t}).\end{eqnarray}$$Thus, we have
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(d[A_{t}^{n}])=n\unicode[STIX]{x1D70F}(A_{t}^{n-1}dA_{t})+\frac{n}{2}\mathop{\sum }_{k=1}^{n-1}\unicode[STIX]{x1D70F}(A_{t}^{n-k-1}dA_{t}\,A_{t}^{k-1}dA_{t}).\end{eqnarray}$$ Now since 
$R$ and 
$S$ are independent from 
$t$, the free Ito’s formula implies
$$\begin{eqnarray}\displaystyle dA_{t}=Rd(U_{t}SU_{t}^{\ast }) & = & \displaystyle R(dU_{t})SU_{t}^{\ast }+RU_{t}d(SU_{t}^{\ast })+R(dU_{t})d(SU_{t}^{\ast })\nonumber\\ \displaystyle & = & \displaystyle R(dU_{t})SU_{t}^{\ast }+RU_{t}S(dU_{t}^{\ast })+R(dU_{t})S(dU_{t}^{\ast }).\nonumber\end{eqnarray}$$But, since
$$\begin{eqnarray}dU_{t}=iU_{t}dB_{t}-{\textstyle \frac{1}{2}}U_{t}\,dt\qquad \text{and}\qquad dU_{t}^{\ast }=-idB_{t}U_{t}^{\ast }-{\textstyle \frac{1}{2}}U_{t}^{\ast }\,dt.\end{eqnarray}$$ Then substituting these equations in the expression of 
$dA_{t}$ we get
$$\begin{eqnarray}\displaystyle dA_{t} & = & \displaystyle R\left(iU_{t}dB_{t}-{\textstyle \frac{1}{2}}U_{t}\,dt\right)SU_{t}^{\ast }+RU_{t}S\left(-idB_{t}U_{t}^{\ast }-{\textstyle \frac{1}{2}}U_{t}^{\ast }\,dt\right)\nonumber\\ \displaystyle & & \displaystyle +\,R\left(iU_{t}dB_{t}-{\textstyle \frac{1}{2}}U_{t}\,dt\right)S\left(-idB_{t}U_{t}^{\ast }-{\textstyle \frac{1}{2}}U_{t}^{\ast }\,dt\right).\nonumber\end{eqnarray}$$The first two terms simplify to
$$\begin{eqnarray}\displaystyle & & \displaystyle iRU_{t}dB_{t}SU_{t}^{\ast }-iRU_{t}SdB_{t}U_{t}^{\ast }-RU_{t}SU_{t}^{\ast }\,dt\nonumber\\ \displaystyle & & \displaystyle \quad =iRU_{t}dB_{t}SU_{t}^{\ast }-iRU_{t}SdB_{t}U_{t}^{\ast }-A_{t}\,dt\nonumber\end{eqnarray}$$while the last term is reduced to
$$\begin{eqnarray}\displaystyle R(iU_{t}dB_{t})S(-idB_{t}U_{t}^{\ast })=RU_{t}dB_{t}SdB_{t}U_{t}^{\ast }=RU_{t}\unicode[STIX]{x1D70F}(S)U_{t}^{\ast }\,dt=\unicode[STIX]{x1D6FD}R\,dt. & & \displaystyle \nonumber\end{eqnarray}$$Thus, we have
$$\begin{eqnarray}dA_{t}=iRU_{t}dB_{t}SU_{t}^{\ast }-iRU_{t}SdB_{t}U_{t}^{\ast }+(\unicode[STIX]{x1D6FD}R-A_{t})\,dt.\end{eqnarray}$$So that,
$$\begin{eqnarray}A_{t}^{n-1}dA_{t}=iA_{t}^{n-1}RU_{t}dB_{t}SU_{t}^{\ast }-iA_{t}^{n-1}RU_{t}SdB_{t}U_{t}^{\ast }+A_{t}^{n-1}(\unicode[STIX]{x1D6FD}R-A_{t})\,dt.\end{eqnarray}$$Since the trace of a stochastic integral is zero, then the first term in equation (2.3) is given by
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(A_{t}^{n-1}dA_{t})=\unicode[STIX]{x1D70F}(A_{t}^{n-1}[\unicode[STIX]{x1D6FD}R-A_{t}])\,dt=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70F}(A_{t}^{n-1}R)-\unicode[STIX]{x1D70F}(A_{t}^{n})]\,dt.\end{eqnarray}$$ Using the trace property and the relations 
$R^{2}=S^{2}=U_{t}U_{t}^{\ast }=1$, we have 
$\unicode[STIX]{x1D70F}(A_{t}^{n-1}R)=\unicode[STIX]{x1D70F}(R)=\unicode[STIX]{x1D6FC}$ if 
$n$ is odd and 
$\unicode[STIX]{x1D70F}(A_{t}^{n-1}R)=\unicode[STIX]{x1D70F}(S)=\unicode[STIX]{x1D6FD}$ otherwise.
Hence, the first term in equation (2.3) is equal to
$$\begin{eqnarray}n\unicode[STIX]{x1D70F}(A_{t}^{n-1}dA_{t})=\left\{\begin{array}{@{}ll@{}}[n\unicode[STIX]{x1D6FD}^{2}-n\unicode[STIX]{x1D70F}(A_{t}^{n})]\,dt\quad & \text{if }n\text{ is even}\\ \text{}[n\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}-n\unicode[STIX]{x1D70F}(A_{t}^{n})]\,dt\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$For the second term in equation (2.3), we shall use the following result.
Lemma 2.2. Let
$$\begin{eqnarray}dZ_{t}=iRU_{t}dB_{t}SU_{t}^{\ast }-iRU_{t}SdB_{t}U_{t}^{\ast }.\end{eqnarray}$$Then
$$\begin{eqnarray}dt\,dZ_{t}=dZ_{t}\,dt=(dt)^{2}=0\end{eqnarray}$$ and for any adapted process 
$V_{t}$, we have
$$\begin{eqnarray}dZ_{t}\,V_{t}\,dZ_{t}=[2R\unicode[STIX]{x1D70F}(RV_{t})-2A_{t}\unicode[STIX]{x1D70F}(A_{t}V_{t})]\,dt.\end{eqnarray}$$Proof. The first statement is a consequence of Itô rules since 
$Z_{t}$ is a stochastic integral. For the last, we expand
$$\begin{eqnarray}\displaystyle dZ_{t}\,V_{t}\,dZ_{t} & = & \displaystyle (iRU_{t}dB_{t}SU_{t}^{\ast }-iRU_{t}SdB_{t}U_{t}^{\ast })V_{t}(iRU_{t}dB_{t}SU_{t}^{\ast }-iRU_{t}SdB_{t}U_{t}^{\ast })\nonumber\\ \displaystyle & = & \displaystyle -RU_{t}dB_{t}SU_{t}^{\ast }V_{t}RU_{t}dB_{t}SU_{t}^{\ast }+RU_{t}dB_{t}SU_{t}^{\ast }V_{t}RU_{t}SdB_{t}U_{t}^{\ast }\nonumber\\ \displaystyle & & \displaystyle +\,RU_{t}SdB_{t}U_{t}^{\ast }V_{t}RU_{t}dB_{t}SU_{t}^{\ast }-RU_{t}SdB_{t}U_{t}^{\ast }V_{t}RU_{t}SdB_{t}U_{t}^{\ast }.\nonumber\end{eqnarray}$$Applying the Itô rule
$$\begin{eqnarray}dB_{t}V_{t}dB_{t}=\unicode[STIX]{x1D70F}(V_{t})\,dt\end{eqnarray}$$to each of these terms yields
$$\begin{eqnarray}\displaystyle dZ_{t}\,V_{t}\,dZ_{t} & = & \displaystyle -RU_{t}\unicode[STIX]{x1D70F}(SU_{t}^{\ast }V_{t}RU_{t})SU_{t}^{\ast }\,dt+RU_{t}\unicode[STIX]{x1D70F}(SU_{t}^{\ast }V_{t}RU_{t}S)U_{t}^{\ast }\,dt\nonumber\\ \displaystyle & & \displaystyle +\,RU_{t}S\unicode[STIX]{x1D70F}(U_{t}^{\ast }V_{t}RU_{t})SU_{t}^{\ast }\,dt-RU_{t}S\unicode[STIX]{x1D70F}(U_{t}^{\ast }V_{t}RU_{t}S)U_{t}^{\ast }\,dt.\nonumber\end{eqnarray}$$ Using the trace property and the relations 
$S^{2}=U_{t}U_{t}^{\ast }=1,A_{t}=RU_{t}SU_{t}^{\ast }$, we get
$$\begin{eqnarray}\displaystyle dZ_{t}\,V_{t}\,dZ_{t}=-A_{t}\unicode[STIX]{x1D70F}(A_{t}V_{t})\,dt+R\unicode[STIX]{x1D70F}(V_{t}R)\,dt+R\unicode[STIX]{x1D70F}(V_{t}R)\,dt-A_{t}\unicode[STIX]{x1D70F}(A_{t}V_{t})\,dt & & \displaystyle \nonumber\end{eqnarray}$$which simplifies to give the equality (2.7).◻
It follows from (2.4) and (2.6) that for 
$n\geqslant 2$ and 
$k\in \{1,\ldots ,n-1\}$,
$$\begin{eqnarray}\displaystyle & & \displaystyle A_{t}^{n-k-1}dA_{t}\,A_{t}^{k-1}dA_{t}\nonumber\\ \displaystyle & & \displaystyle \quad =A_{t}^{n-k-1}[dZ_{t}+(\unicode[STIX]{x1D6FD}R-A_{t})\,dt]A_{t}^{k-1}[dZ_{t}+(\unicode[STIX]{x1D6FD}R-A_{t})\,dt]\nonumber\end{eqnarray}$$which expands into four terms. But by use of Lemma 2.2, the only surviving term is
$$\begin{eqnarray}A_{t}^{n-k-1}dZ_{t}\,A_{t}^{k-1}\,dZ_{t}=A_{t}^{n-k-1}[2R\unicode[STIX]{x1D70F}(RA_{t}^{k-1})-2A_{t}\unicode[STIX]{x1D70F}(A_{t}^{k})]\,dt.\end{eqnarray}$$Taking the trace, we get
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(A_{t}^{n-k-1}dA_{t}\,A_{t}^{k-1}dA_{t})=[2\unicode[STIX]{x1D70F}(RA_{t}^{k-1})\unicode[STIX]{x1D70F}(RA_{t}^{n-k-1})-2\unicode[STIX]{x1D70F}(A_{t}^{k})\unicode[STIX]{x1D70F}(A_{t}^{n-k})]\,dt.\end{eqnarray}$$ Using the same consideration leading to (2.1) and the fact that if 
$n$ is even then 
$k,n-k$ have the same parity and if 
$n$ is odd then 
$k,n-k$ have opposite parity, we have
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(A_{t}^{n-k-1}\,dA_{t}\,A_{t}^{k-1}dA_{t})=\left\{\begin{array}{@{}ll@{}}(2\unicode[STIX]{x1D6FC}^{2}-2\unicode[STIX]{x1D70F}(A_{t}^{k})\unicode[STIX]{x1D70F}(A_{t}^{n-k}))\,dt;\quad & n\text{ even},k\text{ odd}\\ (2\unicode[STIX]{x1D6FD}^{2}-2\unicode[STIX]{x1D70F}(A_{t}^{k})\unicode[STIX]{x1D70F}(A_{t}^{n-k}))\,dt;\quad & n\text{ even},k\text{ even}\\ (2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}-2\unicode[STIX]{x1D70F}(A_{t}^{k})\unicode[STIX]{x1D70F}(A_{t}^{n-k}))\,dt;\quad & n\text{ odd},k\text{ odd}\\ (2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}-2\unicode[STIX]{x1D70F}(A_{t}^{k})\unicode[STIX]{x1D70F}(A_{t}^{n-k}))\,dt;\quad & n\text{ odd},k\text{ even.}\end{array}\right.\end{eqnarray}$$Hence, the second term on the RHS of (2.3) is equal to
$$\begin{eqnarray}\displaystyle \displaystyle \left\{\begin{array}{@{}ll@{}}\left(-n\displaystyle \mathop{\sum }_{k=1}^{n-1}\unicode[STIX]{x1D70F}(A_{t}^{k})\unicode[STIX]{x1D70F}(A_{t}^{n-k})+\frac{n^{2}}{2}\unicode[STIX]{x1D6FC}^{2}+\frac{n(n-2)}{2}\unicode[STIX]{x1D6FD}^{2}\right)\,dt\quad & \text{if }n\text{ is even}\\ \left(-n\displaystyle \mathop{\sum }_{k=1}^{n-1}\unicode[STIX]{x1D70F}(A_{t}^{k})\unicode[STIX]{x1D70F}(A_{t}^{n-k})+n(n-1)\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\right)\,dt\quad & \text{if }n\text{ is odd}\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$which simplifies to
$$\begin{eqnarray}-n\displaystyle \mathop{\sum }_{k=1}^{n-1}\unicode[STIX]{x1D70F}(A_{t}^{k})\unicode[STIX]{x1D70F}(A_{t}^{n-k})+\left\{\begin{array}{@{}ll@{}}\left({\displaystyle \frac{n^{2}}{2}}\unicode[STIX]{x1D6FC}^{2}+{\displaystyle \frac{n(n-2)}{2}}\unicode[STIX]{x1D6FD}^{2}\right)\,dt\quad & \text{if }n\text{ is even}\\ \left(n(n-1)\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\right)\,dt\quad & \text{if }n\text{ is odd}\end{array}\right.\end{eqnarray}$$and hence the desired assertions follow after summing (2.5) and (2.8).◻
2.2 The Herglotz transform of $\unicode[STIX]{x1D708}_{t}$
Here, we derive a PDE governing the Herglotz transform of the spectral measure 
$\unicode[STIX]{x1D708}_{t}$:
$$\begin{eqnarray}H(t,z):=\int _{\mathbb{T}}\frac{\unicode[STIX]{x1D701}+z}{\unicode[STIX]{x1D701}-z}d\unicode[STIX]{x1D708}_{t}(\unicode[STIX]{x1D701})=1+2\mathop{\sum }_{n\geqslant 1}f_{n}(t)z^{n}.\end{eqnarray}$$ Recall that, this is an analytic function on 
$\mathbb{D}$ (the open unit disc of 
$\mathbb{C}$).
Proposition 2.3. The function 
$H(t,z)$ satisfies the PDE
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}H+\frac{z}{2}\unicode[STIX]{x2202}_{z}H^{2}=\frac{2z(\unicode[STIX]{x1D6FC}z^{2}+2\unicode[STIX]{x1D6FD}z+\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D6FD}z^{2}+2\unicode[STIX]{x1D6FC}z+\unicode[STIX]{x1D6FD})}{(1-z^{2})^{3}}.\end{eqnarray}$$Proof. By direct calculation from Proposition 2.1, we have
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{t}H & = & \displaystyle 2\mathop{\sum }_{n\geqslant 1}\unicode[STIX]{x2202}_{t}f_{n}(t)z^{n}\nonumber\\ \displaystyle & = & \displaystyle -2\mathop{\sum }_{n\geqslant 1}nf_{n}z^{n}-2\mathop{\sum }_{n\geqslant 1}n\mathop{\sum }_{k=1}^{n-1}f_{k}f_{n-k}z^{n}+(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})\mathop{\sum }_{n\geqslant 1,~n~\text{even}}n^{2}z^{n}\nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\mathop{\sum }_{n\geqslant 1,~n~\text{odd}}n^{2}z^{n}\nonumber\\ \displaystyle & = & \displaystyle -z\unicode[STIX]{x2202}_{z}H-2\mathop{\sum }_{k\geqslant 1}f_{k}z^{k}\mathop{\sum }_{n\geqslant k+1}nf_{n-k}z^{n-k}+4(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})\frac{z^{2}(1+z^{2})}{(1-z^{2})^{3}}\nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}z\frac{1+6z^{2}+z^{4}}{(1-z^{2})^{3}}\nonumber\\ \displaystyle & = & \displaystyle -z\unicode[STIX]{x2202}_{z}H-4z\frac{H-1}{2}\frac{\unicode[STIX]{x2202}_{z}H}{2}+\frac{2z(\unicode[STIX]{x1D6FC}z^{2}+2\unicode[STIX]{x1D6FD}z+\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D6FD}z^{2}+2\unicode[STIX]{x1D6FC}z+\unicode[STIX]{x1D6FD})}{(1-z^{2})^{3}}\nonumber\\ \displaystyle & = & \displaystyle -zH\unicode[STIX]{x2202}_{z}H+\frac{2z(\unicode[STIX]{x1D6FC}z^{2}+2\unicode[STIX]{x1D6FD}z+\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D6FD}z^{2}+2\unicode[STIX]{x1D6FC}z+\unicode[STIX]{x1D6FD})}{(1-z^{2})^{3}}.\square\nonumber\end{eqnarray}$$2.3 Steady-state solution
As mentioned in the Introduction, it is known from the asymptotic freeness of 
$P$ and 
$U_{t}QU_{t}^{\ast }$ that
Proposition 2.4. The spectral measure 
$\unicode[STIX]{x1D708}_{t}$ of 
$RU_{t}SU_{t}^{\ast }$ converges weakly, as 
$t\rightarrow \infty$, to the free multiplicative convolution of the spectral measures of 
$R$ and 
$USU^{\ast }$, where 
$U\in \mathscr{A}$ is a Haar unitary operator free from 
$\{R,S\}$.
We will see this directly from the PDE (2.9). Let 
$H(\infty ,.)$ be the state solution of (2.9), then it satisfies
$$\begin{eqnarray}\unicode[STIX]{x2202}_{z}H^{2}=\frac{4(\unicode[STIX]{x1D6FC}z^{2}+2\unicode[STIX]{x1D6FD}z+\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D6FD}z^{2}+2\unicode[STIX]{x1D6FC}z+\unicode[STIX]{x1D6FD})}{(1-z^{2})^{3}}.\end{eqnarray}$$ After integration and taking into account 
$H(\infty ,0)=1$, we get
$$\begin{eqnarray}H(\infty ,z)=\sqrt{1+4z\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}(1+z)^{2}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}z}{(1-z^{2})^{2}}},\end{eqnarray}$$ where the principal branch of the square root is taken. On the other hand, the next technical proposition gives an explicit calculation for the Herglotz transform of 
$\unicode[STIX]{x1D708}_{R}\boxtimes \unicode[STIX]{x1D708}_{S}$.
Proposition 2.5. Let 
$\unicode[STIX]{x1D707}=((1+\unicode[STIX]{x1D6FC})/2)\unicode[STIX]{x1D6FF}_{1}+((1-\unicode[STIX]{x1D6FC})/2)\unicode[STIX]{x1D6FF}_{-1}$ and
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}=\left(\frac{1+\unicode[STIX]{x1D6FC}}{2}\unicode[STIX]{x1D6FF}_{1}+\frac{1-\unicode[STIX]{x1D6FC}}{2}\unicode[STIX]{x1D6FF}_{-1}\right)\boxtimes \left(\frac{1+\unicode[STIX]{x1D6FD}}{2}\unicode[STIX]{x1D6FF}_{1}+\frac{1-\unicode[STIX]{x1D6FD}}{2}\unicode[STIX]{x1D6FF}_{-1}\right) & & \displaystyle \nonumber\end{eqnarray}$$ for 
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in (-1,1]$. Then the Herglotz transform of 
$\unicode[STIX]{x1D708}$ is given by
$$\begin{eqnarray}\displaystyle H_{\unicode[STIX]{x1D708}}(z)=H(\infty ,z)=\sqrt{1+4z\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}(1+z)^{2}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}z}{(1-z^{2})^{2}}}. & & \displaystyle \nonumber\end{eqnarray}$$Proof. Using the analytic machinery for multiplicative convolution (see [Reference Dykema, Nica and Voiculescu10]), we have
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{\unicode[STIX]{x1D707}}(z) & = & \displaystyle \frac{z(z+\unicode[STIX]{x1D6FC})}{1-z^{2}},\nonumber\\ \displaystyle \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D707}}(z) & = & \displaystyle \frac{-\unicode[STIX]{x1D6FC}\pm \sqrt{\unicode[STIX]{x1D6FC}^{2}+4z(z+1)}}{2(z+1)},\nonumber\\ \displaystyle S_{\unicode[STIX]{x1D707}}(z) & = & \displaystyle \frac{-\unicode[STIX]{x1D6FC}\pm \sqrt{\unicode[STIX]{x1D6FC}^{2}+4z(z+1)}}{2z}.\nonumber\end{eqnarray}$$So that
$$\begin{eqnarray}\displaystyle S_{\unicode[STIX]{x1D708}}(z) & = & \displaystyle \frac{\left(-\unicode[STIX]{x1D6FC}\pm \sqrt{\unicode[STIX]{x1D6FC}^{2}+4z(z+1)}\right)\left(-\unicode[STIX]{x1D6FD}\pm \sqrt{\unicode[STIX]{x1D6FD}^{2}+4z(z+1)}\right)}{4z^{2}},\nonumber\\ \displaystyle \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}}(z) & = & \displaystyle \frac{\left(-\unicode[STIX]{x1D6FC}\pm \sqrt{\unicode[STIX]{x1D6FC}^{2}+4z(z+1)}\right)\left(-\unicode[STIX]{x1D6FD}\pm \sqrt{\unicode[STIX]{x1D6FD}^{2}+4z(z+1)}\right)}{4z(z+1)},\nonumber\end{eqnarray}$$ and 
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D708}}$ satisfies
$$\begin{eqnarray}\frac{\left(-\unicode[STIX]{x1D6FC}\pm \sqrt{\unicode[STIX]{x1D6FC}^{2}+4\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D708}}+1)}\right)\left(-\unicode[STIX]{x1D6FD}\pm \sqrt{\unicode[STIX]{x1D6FD}^{2}+4\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D708}}+1)}\right)}{4\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D708}}+1)}=z.\end{eqnarray}$$ Letting 
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D708}}+1)$, we get 
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D708}}=(-1\pm \sqrt{1+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}})/2$ and since the Herglotz transform has a positive real part, 
$H_{\unicode[STIX]{x1D708}}=\sqrt{1+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}}$ where 
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}$ is given by
$$\begin{eqnarray}\frac{\left(-\unicode[STIX]{x1D6FC}\pm \sqrt{\unicode[STIX]{x1D6FC}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}}\right)\left(-\unicode[STIX]{x1D6FD}\pm \sqrt{\unicode[STIX]{x1D6FD}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}}\right)}{4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}}=z.\end{eqnarray}$$Or equivalently
$$\begin{eqnarray}-\unicode[STIX]{x1D6FC}\pm \sqrt{\unicode[STIX]{x1D6FC}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}}=z\left(\unicode[STIX]{x1D6FD}\pm \sqrt{\unicode[STIX]{x1D6FD}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}}\right).\end{eqnarray}$$Rearranging this last equality and raising it to the square, we get
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}+z^{2}(\unicode[STIX]{x1D6FD}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}})-(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}z)^{2}=2z\sqrt{(\unicode[STIX]{x1D6FC}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}})(\unicode[STIX]{x1D6FD}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}})}.\end{eqnarray}$$So we raise it to the square once again, to get
$$\begin{eqnarray}[\unicode[STIX]{x1D6FC}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}+z^{2}(\unicode[STIX]{x1D6FD}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}})-(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}z)^{2}]^{2}=4z^{2}(\unicode[STIX]{x1D6FC}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}})(\unicode[STIX]{x1D6FD}^{2}+4\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}).\end{eqnarray}$$Which simplifies to
$$\begin{eqnarray}2(1-z^{2})^{2}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}+[(1-z^{2})(\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FD}^{2}z^{2}-(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}z)^{2})-2z^{2}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}z)^{2}]=0.\end{eqnarray}$$Finally,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}}(z)=\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}z(1+z)^{2}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}z^{2}}{(1-z^{2})^{2}} & & \displaystyle \nonumber\end{eqnarray}$$as desired. ◻
The next proposition provides a Lebesgue decomposition of the spectral measure 
$\unicode[STIX]{x1D708}_{\infty }$.
Proposition 2.6. One has
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{\infty }=a\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}+b\unicode[STIX]{x1D6FF}_{0}+\frac{\sqrt{-(\cos \unicode[STIX]{x1D703}-r_{+})(\cos \unicode[STIX]{x1D703}-r_{-})}}{2\unicode[STIX]{x1D70B}|\text{sin}\unicode[STIX]{x1D703}|}\mathbf{1}_{(\unicode[STIX]{x1D703}_{-},\unicode[STIX]{x1D703}_{+})\cup (-\unicode[STIX]{x1D703}_{+},-\unicode[STIX]{x1D703}_{-})}\,d\unicode[STIX]{x1D703}\end{eqnarray}$$with
$$\begin{eqnarray}\displaystyle & & \displaystyle a=\frac{|\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}|}{2},\qquad b=\frac{|\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}|}{2},\qquad r_{\pm }=-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\pm \sqrt{(1-\unicode[STIX]{x1D6FC}^{2})(1-\unicode[STIX]{x1D6FD}^{2})}\nonumber\\ \displaystyle & & \displaystyle \qquad \text{and}\qquad \unicode[STIX]{x1D703}_{\pm }=\arccos r_{\pm }.\nonumber\end{eqnarray}$$Proof. Writing (2.10) as
$$\begin{eqnarray}H(\infty ,z)=\frac{\sqrt{(1-z^{2})^{2}+4z[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}(1+z)^{2}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}z]}}{(1-z^{2})},\end{eqnarray}$$ it follows that 
$H(\infty ,.)$ admits two simple poles at 
$z=1$ and 
$z=-1$. So that, the decomposition of 
$\unicode[STIX]{x1D708}_{\infty }$ is given by
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{\infty }=a\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}+b\unicode[STIX]{x1D6FF}_{0}+\Re [H(\infty ,e^{i\unicode[STIX]{x1D703}})]\frac{d\unicode[STIX]{x1D703}}{2\unicode[STIX]{x1D70B}},\end{eqnarray}$$ where 
$d\unicode[STIX]{x1D703}$ denotes the (no-normalized) Lebesgue measure on 
$\mathbb{T}=(-\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}]$ and 
$a,b$ are the residue of 
$\frac{1}{2}H(\infty ,.)$ at 
$-1,1$. Thus, we have
$$\begin{eqnarray}\displaystyle a & = & \displaystyle \lim _{z\rightarrow -1}\frac{\sqrt{(1-z^{2})^{2}+4z[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}(1+z)^{2}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}z]}}{2(1+z)}=\frac{|\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}|}{2},\nonumber\\ \displaystyle b & = & \displaystyle \lim _{z\rightarrow 1}\frac{\sqrt{(1-z^{2})^{2}+4z[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}(1+z)^{2}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}z]}}{2(1-z)}=\frac{|\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}|}{2}\nonumber\end{eqnarray}$$and the density is given by direct calculation
$$\begin{eqnarray}\displaystyle \Re [H(\infty ,e^{i\unicode[STIX]{x1D703}})] & = & \displaystyle \Re \left[\sqrt{1+4e^{i\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}(1+e^{i\unicode[STIX]{x1D703}})^{2}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}e^{i\unicode[STIX]{x1D703}}}{(1-e^{2i\unicode[STIX]{x1D703}})^{2}}}\right]\nonumber\\ \displaystyle & = & \displaystyle \Re \left[\sqrt{1+\frac{4\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}e^{i\unicode[STIX]{x1D703}}}{(1-e^{i\unicode[STIX]{x1D703}})^{2}}+\frac{4(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}e^{2i\unicode[STIX]{x1D703}}}{(1-e^{2i\unicode[STIX]{x1D703}})^{2}}}\right]\nonumber\\ \displaystyle & = & \displaystyle \sqrt{1-\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{\sin ^{2}(\unicode[STIX]{x1D703}/2)}-\frac{(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}}{\sin ^{2}\unicode[STIX]{x1D703}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{\sqrt{ sin^{2}\unicode[STIX]{x1D703}-4\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\cos ^{2}(\unicode[STIX]{x1D703}/2)-(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}}}{|\text{sin}\unicode[STIX]{x1D703}|},\nonumber\end{eqnarray}$$where we have used in the last equality the relation
$$\begin{eqnarray}\sin ^{2}\frac{\unicode[STIX]{x1D703}}{2}=\frac{\sin ^{2}\unicode[STIX]{x1D703}}{4\cos ^{2}(\unicode[STIX]{x1D703}/2)}.\end{eqnarray}$$Finally, by use of the basic trigonometric identities:
$$\begin{eqnarray}\cos ^{2}\unicode[STIX]{x1D703}+\sin ^{2}\unicode[STIX]{x1D703}=1\qquad \text{and}\qquad \cos ^{2}\frac{\unicode[STIX]{x1D703}}{2}=\frac{1+\cos \unicode[STIX]{x1D703}}{2},\end{eqnarray}$$the denominator rewrites as
$$\begin{eqnarray}\displaystyle \sin ^{2}\unicode[STIX]{x1D703}-4\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\cos ^{2}\frac{\unicode[STIX]{x1D703}}{2}-(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2} & = & \displaystyle 1-\cos ^{2}\unicode[STIX]{x1D703}-2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\cos \unicode[STIX]{x1D703}-2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}-(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}\nonumber\\ \displaystyle & = & \displaystyle -\cos ^{2}\unicode[STIX]{x1D703}-2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\cos \unicode[STIX]{x1D703}+1-\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FD}^{2}.\nonumber\end{eqnarray}$$ Using the discriminant 
$\unicode[STIX]{x1D6E5}=4(\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FD}^{2}+1-\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FD}^{2})=4(1-\unicode[STIX]{x1D6FC}^{2})(1-\unicode[STIX]{x1D6FD}^{2})\geqslant 0$, we get the factorization 
$-(\cos \unicode[STIX]{x1D703}-r_{+})(\cos \unicode[STIX]{x1D703}-r_{-})$ with
$$\begin{eqnarray}r_{\pm }=-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\pm \sqrt{(1-\unicode[STIX]{x1D6FC}^{2})(1-\unicode[STIX]{x1D6FD}^{2})}.\square\end{eqnarray}$$Remark 2.7. It should be noted that this measure appears in [Reference Hiai and Petz13, Example 4.5] as the distribution of 
$e^{i\unicode[STIX]{x1D70B}P}e^{-i\unicode[STIX]{x1D70B}Q}$ for a pair of free projections 
$\{P,Q\}$ in 
$\mathscr{A}$. In particular, when 
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=0$ (i.e., 
$\unicode[STIX]{x1D70F}(P)=\unicode[STIX]{x1D70F}(Q)=1/2$), it coincides with the uniform measure on 
$\mathbb{T}$.
3 Relationship between $\unicode[STIX]{x1D707}_{t}$ and $\unicode[STIX]{x1D708}_{t}$
Keep the symbols 
$P,Q,R,S,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},a,b$ and 
$\unicode[STIX]{x1D707}_{t},\unicode[STIX]{x1D708}_{t}$ as above. In what follows 
$P,Q$ and 
$R,S$ are associated. Our goal here is to derive a relationship between 
$\unicode[STIX]{x1D707}_{t}$ and 
$\unicode[STIX]{x1D708}_{t}$ and give more detailed properties of 
$\unicode[STIX]{x1D708}_{t}$. Here is a relationship between the corresponding sequence of moments.
Proposition 3.1. For any 
$n\geqslant 1$, one has:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}([PU_{t}QU_{t}^{\ast }P]^{n}) & = & \displaystyle \frac{1}{2^{2n+1}}\binom{2n}{n}+\frac{\unicode[STIX]{x1D70F}(R+S)}{4}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2^{2n}}\mathop{\sum }_{k=1}^{n}\binom{2n}{n-k}\unicode[STIX]{x1D70F}((RU_{t}SU_{t}^{\ast })^{k}).\end{eqnarray}$$Proof. Since 
$P$ is idempotent and since 
$\unicode[STIX]{x1D70F}$ is a trace, we write
$$\begin{eqnarray}\unicode[STIX]{x1D70F}[(PU_{t}QU_{t}^{\ast }P)^{n}]=\unicode[STIX]{x1D70F}[(PU_{t}QU_{t}^{\ast })^{n}]=\frac{1}{2^{2n}}\unicode[STIX]{x1D70F}[((\mathbf{1}+R)U_{t}(\mathbf{1}+S)U_{t}^{\ast })^{n}].\end{eqnarray}$$ Let 
$\tilde{S}:=U_{t}SU_{t}^{\ast }$. Then writing
$$\begin{eqnarray}(\mathbf{1}+R)U_{t}(\mathbf{1}+S)U_{t}^{\ast }=(\mathbf{1}+R)(\mathbf{1}+\tilde{S})\end{eqnarray}$$ one easily can see that the same enumeration techniques used in [Reference Demni, Hamdi and Hmidi7, Proposition 4.1] to expand 
$\unicode[STIX]{x1D70F}[((\mathbf{1}+R)(\mathbf{1}+\tilde{S}))^{n}]$ remain valid, but here we will take into account the contribution of words formed by an odd number of letters. Using the trace property and the relations 
$R^{2}=\tilde{S}^{2}=\mathbf{1}$, this contribution is 
$\unicode[STIX]{x1D70F}(R)+\unicode[STIX]{x1D70F}(S)$ up to a positive integer 
$N$. By letting 
$R=S$ and using the expansion in [Reference Demni, Hamdi and Hmidi7, p. 1366], we get 
$2N=2^{2n-1}$ and hence the desired equality follows.◻
Let
$$\begin{eqnarray}G(t,z):=\frac{1}{z}+\mathop{\sum }_{n\geqslant 1}\frac{\unicode[STIX]{x1D70F}[(PU_{t}QU_{t}^{\ast }P)^{n}]}{z^{n+1}},\quad t\geqslant 0,|z|>1,\end{eqnarray}$$ be the Cauchy transform of the process 
$X_{t}$. The following corollary gives a relationship between 
$G$ and the Herglotz transform of 
$\unicode[STIX]{x1D708}_{t}$.
Corollary 3.2. One has
$$\begin{eqnarray}G(t,z)=\frac{1}{2z}+\frac{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}{4z(z-1)}+\frac{H(t,g(z))}{2\sqrt{z^{2}-z}},\quad t\geqslant 0,|z|>1,\end{eqnarray}$$whereFootnote 1
$$\begin{eqnarray}g(z)=2z-1+2\sqrt{z^{2}-z}.\end{eqnarray}$$Proof. We will prove the following equivalent relation
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D707}_{t}}(z)=\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}+2)z-2}{4(1-z)}+\frac{H(t,g(1/z))}{2\sqrt{1-z}},\quad t\geqslant 0,|z|<1,\end{eqnarray}$$ satisfied by the moment generating function of the process 
$X_{t}$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D707}_{t}}(z):=\mathop{\sum }_{n\geqslant 1}\unicode[STIX]{x1D70F}[(PU_{t}QU_{t}^{\ast }P)^{n}]z^{n},\quad t\geqslant 0,|z|<1.\end{eqnarray}$$ Before going into the details, recall from [Reference Demni, Hamdi and Hmidi7, p. 1359] that 
$|g(1/z)|\leqslant |z|<1$ in the open unit disc, then this last relation makes sense for all 
$|z|<1$. Now multiplying (3.1) by 
$z^{n}$ and summing over 
$n\geqslant 1$, we get
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{\unicode[STIX]{x1D707}_{t}}(z)=\frac{1}{2\sqrt{1-z}}-\frac{1}{2}+\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})z}{4(1-z)}+\mathop{\sum }_{n\geqslant 1}\frac{z^{n}}{2^{2n}}\mathop{\sum }_{k=1}^{n}\binom{2n}{n-k}\unicode[STIX]{x1D70F}[(RU_{t}SU_{t}^{\ast })^{k}]. & & \displaystyle \nonumber\end{eqnarray}$$ But, this last term rewrites, after permutation of sums and reindexing 
$j=n-k$, as
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n\geqslant 1}\frac{z^{n}}{2^{2n}}\mathop{\sum }_{k=1}^{n}\binom{2n}{n-k}\unicode[STIX]{x1D70F}[(RU_{t}SU_{t}^{\ast })^{k}]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k\geqslant 1}\unicode[STIX]{x1D70F}[(RU_{t}SU_{t}^{\ast })^{k}]\mathop{\sum }_{j\geqslant 0}\frac{z^{j+k}}{2^{2j+2k}}\binom{2j+2k}{j}.\nonumber\end{eqnarray}$$Using the identity (see, e.g., [Reference Demni, Hamdi and Hmidi7])
$$\begin{eqnarray}\mathop{\sum }_{j\geqslant 0}\binom{2j+2k}{j}\frac{z^{j}}{2^{2j}}=\frac{2^{2k}}{\sqrt{1-z}}(1+\sqrt{1-z})^{-2k},\quad |z|<1,\end{eqnarray}$$we get
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{\unicode[STIX]{x1D707}_{t}}(z) & = & \displaystyle \frac{1}{2\sqrt{1-z}}-\frac{1}{2}+\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})z}{4(1-z)}+\frac{1}{\sqrt{1-z}}\mathop{\sum }_{k\geqslant 1}\frac{\unicode[STIX]{x1D70F}[(RU_{t}SU_{t}^{\ast })^{k}]z^{k}}{(1+\sqrt{1-z})^{2k}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2\sqrt{1-z}}-\frac{1}{2}+\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})z}{4(1-z)}+\frac{1}{\sqrt{1-z}}\frac{H(t,g(1/z))-1}{2}\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{2}+\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})z}{4(1-z)}+\frac{H(t,g(1/z))}{2\sqrt{1-z}},\nonumber\end{eqnarray}$$which proves the corollary. ◻
We are now ready to prove the relationship between the spectral measure of 
$X_{t}$ and 
$Y_{t}$: 
$\unicode[STIX]{x1D707}_{t}\leftrightsquigarrow \unicode[STIX]{x1D708}_{t}$.
Theorem 3.3. Let 
$\tilde{\unicode[STIX]{x1D707}}_{t}(d\unicode[STIX]{x1D703})$ be the positive measure on 
$[0,\unicode[STIX]{x1D70B}]$ obtained from 
$\unicode[STIX]{x1D707}_{t}(dx)$ via the variable change 
$x=\cos ^{2}(\unicode[STIX]{x1D703}/2)$ and
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D707}}_{t}:={\textstyle \frac{1}{2}}(\tilde{\unicode[STIX]{x1D707}}_{t}+(\tilde{\unicode[STIX]{x1D707}}_{t}|_{(0,\unicode[STIX]{x1D70B})})\circ j^{-1})\end{eqnarray}$$ its symmetrization on 
$(-\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B})$ with the mapping 
$j:\unicode[STIX]{x1D703}\in (0,\unicode[STIX]{x1D70B})\mapsto -\unicode[STIX]{x1D703}\in (-\unicode[STIX]{x1D70B},0)$. Then, the two measures 
$\unicode[STIX]{x1D707}_{t}$ and 
$\unicode[STIX]{x1D708}_{t}$ are related via
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{t}=2\hat{\unicode[STIX]{x1D707}}_{t}-\frac{2-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}}{2}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}-\frac{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}{2}\unicode[STIX]{x1D6FF}_{0}.\end{eqnarray}$$Proof. By (3.2), we have
$$\begin{eqnarray}\displaystyle H(t,g(z))=2\sqrt{z^{2}-z}\left(G(t,z)-\frac{2-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}}{4z}-\frac{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}{4(z-1)}\right). & & \displaystyle \nonumber\end{eqnarray}$$ Letting 
$\tilde{\unicode[STIX]{x1D707}}_{t}(d\unicode[STIX]{x1D703})=\unicode[STIX]{x1D707}_{t}(dx)$ with 
$x=\cos ^{2}(\unicode[STIX]{x1D703}/2),\unicode[STIX]{x1D703}\in [0,\unicode[STIX]{x1D70B}]$, we get
$$\begin{eqnarray}\displaystyle H(t,g(z)) & = & \displaystyle -2\sqrt{z^{2}-z}\left(\int _{0}^{\unicode[STIX]{x1D70B}}\frac{1}{z-\cos ^{2}(\unicode[STIX]{x1D703}/2)}\tilde{\unicode[STIX]{x1D707}}_{t}(d\unicode[STIX]{x1D703})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{2-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}}{4z}-\frac{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}{4(z-1)}\right).\nonumber\end{eqnarray}$$Next, we perform the variable change
$$\begin{eqnarray}\unicode[STIX]{x1D701}:=g(z)=2z-1+2\sqrt{z^{2}-z}\quad \Leftrightarrow \quad z=\frac{2+\unicode[STIX]{x1D701}+\unicode[STIX]{x1D701}^{-1}}{4},\end{eqnarray}$$to get
$$\begin{eqnarray}\displaystyle H(t,\unicode[STIX]{x1D701}) & = & \displaystyle \frac{\unicode[STIX]{x1D701}^{-1}-\unicode[STIX]{x1D701}}{2}\left(\int _{0}^{\unicode[STIX]{x1D70B}}\frac{1}{\frac{(2+\unicode[STIX]{x1D701}+\unicode[STIX]{x1D701}^{-1})}{4}-\cos ^{2}(\unicode[STIX]{x1D703}/2)}\tilde{\unicode[STIX]{x1D707}}_{t}(d\unicode[STIX]{x1D703})-\frac{2-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}}{2+\unicode[STIX]{x1D701}+\unicode[STIX]{x1D701}^{-1}}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}{-2+\unicode[STIX]{x1D701}+\unicode[STIX]{x1D701}^{-1}}\vphantom{\frac{1}{\frac{(2+\unicode[STIX]{x1D701}+\unicode[STIX]{x1D701}^{-1})}{4}-\cos ^{2}(\unicode[STIX]{x1D703}/2)}}\right)\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\unicode[STIX]{x1D70B}}\frac{2(\unicode[STIX]{x1D701}^{-1}-\unicode[STIX]{x1D701})}{2+\unicode[STIX]{x1D701}+\unicode[STIX]{x1D701}^{-1}-4\cos ^{2}(\unicode[STIX]{x1D703}/2)}\tilde{\unicode[STIX]{x1D707}}_{t}(d\unicode[STIX]{x1D703})-\frac{(2-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})(1-\unicode[STIX]{x1D701})}{2(1+\unicode[STIX]{x1D701})}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})(1+\unicode[STIX]{x1D701})}{2(1-\unicode[STIX]{x1D701})}.\nonumber\end{eqnarray}$$But since
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D701}^{-1}-\unicode[STIX]{x1D701}}{2+\unicode[STIX]{x1D701}+\unicode[STIX]{x1D701}^{-1}-4\cos ^{2}(\unicode[STIX]{x1D703}/2)} & = & \displaystyle \frac{\unicode[STIX]{x1D701}^{-1}-\unicode[STIX]{x1D701}}{\unicode[STIX]{x1D701}+\unicode[STIX]{x1D701}^{-1}-2\cos \unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1-\unicode[STIX]{x1D701}^{2}}{\unicode[STIX]{x1D701}^{2}-2\unicode[STIX]{x1D701}\cos \unicode[STIX]{x1D703}+1}\nonumber\\ \displaystyle & = & \displaystyle \frac{e^{i\unicode[STIX]{x1D703}}}{e^{i\unicode[STIX]{x1D703}}-\unicode[STIX]{x1D701}}+\frac{e^{i\unicode[STIX]{x1D703}}}{e^{-i\unicode[STIX]{x1D703}}-\unicode[STIX]{x1D701}}-1,\nonumber\end{eqnarray}$$then
$$\begin{eqnarray}\displaystyle H(t,\unicode[STIX]{x1D701}) & = & \displaystyle 2\int _{0}^{\unicode[STIX]{x1D70B}}\left(\frac{e^{i\unicode[STIX]{x1D703}}}{e^{i\unicode[STIX]{x1D703}}-\unicode[STIX]{x1D701}}+\frac{e^{-i\unicode[STIX]{x1D703}}}{e^{-i\unicode[STIX]{x1D703}}-\unicode[STIX]{x1D701}}-1\right)\tilde{\unicode[STIX]{x1D707}}_{t}(d\unicode[STIX]{x1D703})-\frac{(2-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})(1-\unicode[STIX]{x1D701})}{2(1+\unicode[STIX]{x1D701})}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})(1+\unicode[STIX]{x1D701})}{2(1-\unicode[STIX]{x1D701})}.\nonumber\end{eqnarray}$$ Thus, using the symmetrization 
$\hat{\unicode[STIX]{x1D707}}_{t}:={\textstyle \frac{1}{2}}(\tilde{\unicode[STIX]{x1D707}}_{t}+(\tilde{\unicode[STIX]{x1D707}}_{t}|_{(0,\unicode[STIX]{x1D70B})})\circ j^{-1})$ with 
$j:\unicode[STIX]{x1D703}\in (0,\unicode[STIX]{x1D70B})\mapsto -\unicode[STIX]{x1D703}\in (-\unicode[STIX]{x1D70B},0)$, we get
$$\begin{eqnarray}H(t,\unicode[STIX]{x1D701})=\int _{-\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D70B}}\frac{e^{i\unicode[STIX]{x1D703}}+\unicode[STIX]{x1D701}}{e^{i\unicode[STIX]{x1D703}}-\unicode[STIX]{x1D701}}\left(2\hat{\unicode[STIX]{x1D707}}_{t}-\frac{2-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}}{2}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}-\frac{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}{2}\unicode[STIX]{x1D6FF}_{0}\right)(d\unicode[STIX]{x1D703}).\end{eqnarray}$$This proves the theorem. ◻
Remark 3.4. The relationship 
$\unicode[STIX]{x1D707}_{t}\leftrightsquigarrow \unicode[STIX]{x1D708}_{t}$ enables us, in particular, to retrieve the decomposition of 
$\unicode[STIX]{x1D708}_{\infty }$ already obtained in Section 2 from the spectral measure 
$\unicode[STIX]{x1D707}_{\infty }$ (given by the free multiplicative convolution of the spectral measure of 
$P$ and 
$UQU^{\ast }$ with 
$U$ is a Haar unitary free from 
$\{P,Q\}$ (see, [Reference Dykema, Nica and Voiculescu10, Example 3.6.7])). Indeed, we have 
$\hat{\unicode[STIX]{x1D6FF}_{0}}=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}},\hat{\unicode[STIX]{x1D6FF}_{1}}=\unicode[STIX]{x1D6FF}_{0}$ and if 
$\unicode[STIX]{x1D707}_{t}$ has the density 
$h(x)$ with respect to 
$dx$ on 
$[0,1]$, then 
$\unicode[STIX]{x1D708}_{t}$ has the density 
${\hat{h}}(\unicode[STIX]{x1D703})$ with respect to the (no-normalized) Lebesgue measure 
$d\unicode[STIX]{x1D703}$ on 
$\mathbb{T}=(-\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}]$ with 
${\hat{h}}(\unicode[STIX]{x1D703})=h(\cos ^{2}(\unicode[STIX]{x1D703}/2))|\sin \unicode[STIX]{x1D703}|/4$.
Corollary 3.5. For every 
$t>0$ and 
$z\in \mathbb{D}$, we have
$$\begin{eqnarray}H(t,z)=2L(t,z)+a\frac{1-z}{1+z}+b\frac{1+z}{1-z},\end{eqnarray}$$ where 
$L(t,z)$ is the function defined in [Reference Izumi and Ueda15, Section 3] by
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D70B}}\frac{e^{i\unicode[STIX]{x1D703}}+z}{e^{i\unicode[STIX]{x1D703}}-z}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,(\hat{\unicode[STIX]{x1D707}_{t}}-(1-\min \{\unicode[STIX]{x1D70F}(P),\unicode[STIX]{x1D70F}(Q)\})\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}-\max \{\unicode[STIX]{x1D70F}(P)+\unicode[STIX]{x1D70F}(Q)-1,0\}\unicode[STIX]{x1D6FF}_{0})(d\unicode[STIX]{x1D703}).\nonumber\end{eqnarray}$$Proof. We can easily check the result from (3.4) by substituting 
$\unicode[STIX]{x1D70F}(P)=(1+\unicode[STIX]{x1D6FC})/2$, 
$\unicode[STIX]{x1D70F}(Q)=(1+\unicode[STIX]{x1D6FD})/2$ into the expression of 
$L(t,z)$. Then, we obtain
$$\begin{eqnarray}\displaystyle L(t,z) & = & \displaystyle \frac{1}{2}\int _{-\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D70B}}\frac{e^{i\unicode[STIX]{x1D703}}+z}{e^{i\unicode[STIX]{x1D703}}-z}(2\hat{\unicode[STIX]{x1D707}_{t}}-(1-\min \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\})\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}-\max \{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD},0\}\unicode[STIX]{x1D6FF}_{0})(d\unicode[STIX]{x1D703})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\int _{-\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D70B}}\frac{e^{i\unicode[STIX]{x1D703}}+z}{e^{i\unicode[STIX]{x1D703}}-z}\left(2\hat{\unicode[STIX]{x1D707}_{t}}-\frac{2-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}+|\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}|}{2}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}+|\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}|}{2}\unicode[STIX]{x1D6FF}_{0}\right)(d\unicode[STIX]{x1D703})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\left(H(t,z)-a\frac{1-z}{1+z}-b\frac{1+z}{1-z}\right).\square\nonumber\end{eqnarray}$$Remark 3.6. Note that, from the PDE (3.2) of [Reference Izumi and Ueda15], one easily sees that the function
$$\begin{eqnarray}2L(t,z)+a\frac{1-z}{1+z}+b\frac{1+z}{1-z}\end{eqnarray}$$ solves the same PDE (2.9) as 
$H(t,z)$ and therefore, by uniqueness of solutions in the class of analytic function on the unit disc, we deduce the result of Corollary 3.5. This means that Theorem 3.3 can quite easily be deduced from Proposition 2.3 and [Reference Izumi and Ueda15, Section 3]. Nevertheless, the moments formula presented in Proposition 3.1 is of independent interest as it explains the appearance of the operator 
$RU_{t}SU_{t}^{\ast }$ and so it gives a more natural presentation of the result of Theorem 3.3.
From Corollary 3.5, the measure 
$\unicode[STIX]{x1D70E}_{t}:=\unicode[STIX]{x1D708}_{t}-a\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}-b\unicode[STIX]{x1D6FF}_{0}$ rewrites as
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{t}=2[\hat{\unicode[STIX]{x1D707}_{t}}-(1-\min \{\unicode[STIX]{x1D70F}(P),\unicode[STIX]{x1D70F}(Q)\})\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}-\max \{\unicode[STIX]{x1D70F}(P)+\unicode[STIX]{x1D70F}(Q)-1,0\}\unicode[STIX]{x1D6FF}_{0}].\end{eqnarray}$$ Thus, by virtue of [Reference Izumi and Ueda15, Proposition 3.1], we get the following descriptions for the measure 
$\unicode[STIX]{x1D708}_{t}$.
Corollary 3.7. For every 
$t>0$, the positive measure 
$\unicode[STIX]{x1D70E}_{t}$ has no atom at both 0 and 
$\unicode[STIX]{x1D70B}$. Moreover, at 
$t=0$, we have 
$\unicode[STIX]{x1D70E}_{0}\{0\}\geqslant 0$ and 
$\unicode[STIX]{x1D70E}_{0}\{\unicode[STIX]{x1D70B}\}\geqslant 0$ with equalities (i.e., 
$\unicode[STIX]{x1D70E}_{0}$ has no atom at both 0 and 
$\unicode[STIX]{x1D70B}$), if and only if the projections 
$P$ and 
$Q$ are in generic position.
4 Subordination for the liberation of symmetries
The aim of this section is to derive a subordination relation for the Herglotz transform 
$H(t,z)$ and give an explicit formula for its unique subordinate family. For every 
$t\geqslant 0$ and 
$|z|<1$, define the functionFootnote 2
$$\begin{eqnarray}K(t,z):=\sqrt{H(t,z)^{2}-\left(a\frac{1-z}{1+z}+b\frac{1+z}{1-z}\right)^{2}}.\end{eqnarray}$$ This is an analytic function in 
$\mathbb{D}$ with positive real part. Indeed,
$$\begin{eqnarray}H(t,z)^{2}-\left(a\frac{1-z}{1+z}+b\frac{1+z}{1-z}\right)^{2},\quad |z|<1\end{eqnarray}$$ cannot take negative value in 
$\mathbb{D}$ since the two measures 
$\unicode[STIX]{x1D708}_{t}-a\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}-b\unicode[STIX]{x1D6FF}_{0}$ and 
$\unicode[STIX]{x1D708}_{t}+a\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}+b\unicode[STIX]{x1D6FF}_{0}$ are finite positive measure in 
$\mathbb{T}$ (see Corollary 3.7). Thus, according to the Herglotz theorem (see [Reference Cima, Matheson and Ross3, Theorem 1.8.9]), 
$K(t,z)$ has the following integral representation
$$\begin{eqnarray}\displaystyle K(t,z)=\int _{\mathbb{T}}\frac{\unicode[STIX]{x1D701}+z}{\unicode[STIX]{x1D701}-z}\,d\unicode[STIX]{x1D6FE}_{t}(\unicode[STIX]{x1D701}) & & \displaystyle \nonumber\end{eqnarray}$$ for some probability measure 
$\unicode[STIX]{x1D6FE}_{t}$ on 
$\mathbb{T}$. The following result is an immediate consequence of Corollary 3.5 and [Reference Izumi and Ueda15, Proposition 3.1].
Corollary 4.1. There exists a unique subordinate family of conformal self-maps 
$\unicode[STIX]{x1D702}_{t}$ on 
$\mathbb{D}$ such that the subordination relation
$$\begin{eqnarray}K(t,z)=K(0,\unicode[STIX]{x1D702}_{t}(z))\end{eqnarray}$$ holds for any 
$z\in \mathbb{D}$.
Set 
$\unicode[STIX]{x1D719}_{t}:\unicode[STIX]{x1D6FA}_{t}:=\unicode[STIX]{x1D702}_{t}(\mathbb{D}){\twoheadrightarrow}\mathbb{D}$ the inverse function of 
$\unicode[STIX]{x1D702}_{t}$. Then, 
$\unicode[STIX]{x1D719}_{t}$ satisfies the radial Loewner ODE driven by the probability measure 
$\unicode[STIX]{x1D708}_{t}$ (see [Reference Izumi and Ueda15, Equation (3.5)])
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D719}_{t}=\unicode[STIX]{x1D719}_{t}H(t,\unicode[STIX]{x1D719}_{t}),\qquad \unicode[STIX]{x1D719}_{0}(z)=z.\end{eqnarray}$$ The next proposition gives an explicit expression for the transformation 
$\unicode[STIX]{x1D719}_{t}$.
Proposition 4.2. For any 
$t\geqslant 0$ and 
$z\in \unicode[STIX]{x1D6FA}_{t}\cap \mathbb{R}$, we have
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{t}(z)=\frac{w_{t}(y)-1}{w_{t}(y)+1},\qquad y=\frac{1+z}{1-z} & & \displaystyle \nonumber\end{eqnarray}$$with
$$\begin{eqnarray}\displaystyle w_{t}(y)=\sqrt{\frac{(b^{2}-a^{2}-c+de^{t\sqrt{c}})^{2}-4a^{2}c}{(b^{2}-a^{2}+c+de^{t\sqrt{c}})^{2}-4b^{2}c}}, & & \displaystyle \nonumber\end{eqnarray}$$ where 
$c=c(z):=K(0,z)^{2}+\max \{\unicode[STIX]{x1D6FC}^{2},\unicode[STIX]{x1D6FD}^{2}\}$ and
$$\begin{eqnarray}\displaystyle d=d(z):=-c(z)-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}+\frac{2c(z)-2y\sqrt{c(z)}H(0,z)}{1-y^{2}}. & & \displaystyle \nonumber\end{eqnarray}$$Proof. In order to make easier computations, we use the Möbius transform
$$\begin{eqnarray}\displaystyle z\mapsto y=\frac{1+z}{1-z} & & \displaystyle \nonumber\end{eqnarray}$$ to introduce the function 
$F(t,y):=H(t,z)$. Since 
$dy/dz=2/(1-z)^{2}$, the PDE (2.9) becomes
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}F+\frac{y^{2}-1}{4}\unicode[STIX]{x2202}_{y}F^{2}=\frac{(y^{2}-1)}{8y^{3}}((\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})^{2}y^{4}-(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}).\end{eqnarray}$$ Then, the characteristic curve 
$t\mapsto (w_{t}(z),F(t,w_{t}(z)))$ associated with the PDE (4.4) satisfies the system of ODEs:
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}w_{t}={\textstyle \frac{1}{2}}(w_{t}^{2}-1)F(t,w_{t}),\qquad w_{0}(y)=y, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}[F(t,w_{t})]={\displaystyle \frac{(w_{t}^{2}-1)}{8w_{t}^{3}}}((\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})^{2}w_{t}^{4}-(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}), & \displaystyle\end{eqnarray}$$with
$$\begin{eqnarray}\displaystyle w_{t}(y):=\frac{1+\unicode[STIX]{x1D719}_{t}(z)}{1-\unicode[STIX]{x1D719}_{t}(z)}. & & \displaystyle \nonumber\end{eqnarray}$$Combining the two last ODEs, we get
$$\begin{eqnarray}\displaystyle F\unicode[STIX]{x2202}_{t}F=\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})^{2}w_{t}^{4}-(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}}{4w_{t}^{3}}\unicode[STIX]{x2202}_{t}w_{t}. & & \displaystyle \nonumber\end{eqnarray}$$ Hence, integrating with respect to 
$t$, we get
$$\begin{eqnarray}\displaystyle F(t,w_{t}(y))^{2} & = & \displaystyle F(0,y)^{2}+\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})^{2}w_{t}(y)^{4}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}}{4w_{t}(y)^{2}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})^{2}y^{4}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}}{4y^{2}}\nonumber\\ \displaystyle & = & \displaystyle F(0,y)^{2}+\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})^{2}w_{t}(y)^{4}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}}{4w_{t}(y)^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,1-F(\infty ,y)^{2}-\frac{\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2}}{2}.\nonumber\end{eqnarray}$$Consequently, the RHS of (4.5) rewrites as
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{w_{t}(y)^{2}-1}{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\sqrt{1+F(0,y)^{2}-F(\infty ,y)^{2}-\frac{\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2}}{2}+\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})^{2}w_{t}(y)^{4}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}}{4w_{t}(y)^{2}}}\nonumber\\ \displaystyle & & \displaystyle =\frac{w_{t}(y)^{2}-1}{2w_{t}(y)}\sqrt{b^{2}w_{t}(y)^{4}+[1+F(0,y)^{2}-F(\infty ,y)^{2}-a^{2}-b^{2}]w_{t}(y)^{2}+a^{2}}.\nonumber\end{eqnarray}$$ Let 
$u_{t}(y):=1-w_{t}^{2}(y)$, and set
$$\begin{eqnarray}\displaystyle c & = & \displaystyle 1+F(0,y)^{2}-F(\infty ,y)^{2},\nonumber\\ \displaystyle c_{1} & = & \displaystyle c+b^{2}-a^{2}=c+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\nonumber\\ \displaystyle c_{2} & = & \displaystyle b^{2}=\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})^{2}}{4}.\nonumber\end{eqnarray}$$Then, we transform the ODE (4.5) into
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}u_{t}=u_{t}\sqrt{c-c_{1}u_{t}+c_{2}u_{t}^{2}}.\end{eqnarray}$$In order to solve this last ODE, we are lead to compute the indefinite integral
$$\begin{eqnarray}\displaystyle \int \frac{du}{u\sqrt{c-c_{1}u+c_{2}u^{2}}}. & & \displaystyle \nonumber\end{eqnarray}$$Since
$$\begin{eqnarray}\displaystyle c & = & \displaystyle F(0,y)^{2}-\frac{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})^{2}y^{4}+(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})^{2}}{4y^{2}}+\frac{\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2}}{2}\nonumber\\ \displaystyle & = & \displaystyle F(0,y)^{2}-\left(\frac{|\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}|y^{2}+|\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}|}{2y}\right)^{2}+\frac{\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2}+|\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FD}^{2}|}{2}\nonumber\\ \displaystyle & = & \displaystyle F(0,y)^{2}-\left(\frac{by^{2}+a}{y}\right)^{2}+\max \{\unicode[STIX]{x1D6FC}^{2},\unicode[STIX]{x1D6FD}^{2}\}\nonumber\\ \displaystyle & = & \displaystyle K(0,z)^{2}+\max \{\unicode[STIX]{x1D6FC}^{2},\unicode[STIX]{x1D6FD}^{2}\},\nonumber\end{eqnarray}$$we easily see that
$$\begin{eqnarray}\displaystyle c_{1}^{2}-4cc_{2}=c^{2}+2c\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}+(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})^{2}-c(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})^{2}=(c-\unicode[STIX]{x1D6FC}^{2})(c-\unicode[STIX]{x1D6FD}^{2})\geqslant 0. & & \displaystyle \nonumber\end{eqnarray}$$Hence (see the proof in [Reference Demni and Hmidi8, Theorem 3]), we have
$$\begin{eqnarray}\displaystyle \int \frac{du}{u\sqrt{c-c_{1}u+c_{2}u^{2}}}=\frac{1}{\sqrt{c}}\ln \frac{2c-c_{1}u-2\sqrt{c}\sqrt{c-c_{1}u+c_{2}u^{2}}}{|u|}. & & \displaystyle \nonumber\end{eqnarray}$$It follows that,
$$\begin{eqnarray}\displaystyle \frac{2c-c_{1}u_{t}(y)-2\sqrt{c}\sqrt{c-c_{1}u_{t}(y)+c_{2}u_{t}(y)^{2}}}{|u_{t}(y)|}=de^{t\sqrt{c}} & & \displaystyle \nonumber\end{eqnarray}$$ for some 
$d=d(y,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$ and hence
$$\begin{eqnarray}2c-(c_{1}+\unicode[STIX]{x1D716}de^{t\sqrt{c}})u_{t}(y)=2\sqrt{c}\sqrt{c-c_{1}u_{t}(y)+c_{2}u_{t}(y)^{2}},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D716}$ is the sign of 
$u$. Raising this equality to the square and rearranging it, we get
$$\begin{eqnarray}\displaystyle [(c_{1}+\unicode[STIX]{x1D716}de^{t\sqrt{c}})^{2}-4cc_{2}]u_{t}(y)=4c\unicode[STIX]{x1D716}de^{t\sqrt{c}}. & & \displaystyle \nonumber\end{eqnarray}$$Equivalently,
$$\begin{eqnarray}\displaystyle u_{t}(y)=\frac{4c\tilde{d}e^{t\sqrt{c}}}{(c_{1}+\tilde{d}e^{t\sqrt{c}})^{2}-4cc_{2}} & & \displaystyle \nonumber\end{eqnarray}$$ with 
$\tilde{d}=\unicode[STIX]{x1D716}d$. Hence
$$\begin{eqnarray}\displaystyle w_{t}(y)^{2} & = & \displaystyle \frac{(c_{1}+\tilde{d}e^{t\sqrt{c}})^{2}-4cc_{2}-4c\tilde{d}e^{t\sqrt{c}}}{(c_{1}+\tilde{d}e^{t\sqrt{c}})^{2}-4cc_{2}}\nonumber\\ \displaystyle & = & \displaystyle \frac{(b^{2}-a^{2}+c+\tilde{d}e^{t\sqrt{c}})^{2}-4cb^{2}-4c\tilde{d}e^{t\sqrt{c}}}{(b^{2}-a^{2}+c+\tilde{d}e^{t\sqrt{c}})^{2}-4cb^{2}}\nonumber\\ \displaystyle & = & \displaystyle \frac{(b^{2}-a^{2}-c+\tilde{d}e^{t\sqrt{c}})^{2}-4ca^{2}}{(b^{2}-a^{2}+c+\tilde{d}e^{t\sqrt{c}})^{2}-4cb^{2}}.\nonumber\end{eqnarray}$$ Finally, in order to find the value of 
$\tilde{d}$, we check the equality (4.8) for 
$t=0$, we get
$$\begin{eqnarray}\displaystyle 2c-(c_{1}+\tilde{d})u_{0}=2\sqrt{c}\sqrt{c-c_{1}u_{0}+c_{2}u_{0}^{2}}, & & \displaystyle \nonumber\end{eqnarray}$$ where 
$u_{0}:=u_{0}(y)=1-w_{0}(y)^{2}=1-y^{2}$. From (4.5) and (4.7), we can see that
$$\begin{eqnarray}\displaystyle \sqrt{c-c_{1}u_{0}+c_{2}u_{0}^{2}}=w_{0}(y)F\left(0,w_{0}(y)\right)=yF(0,y). & & \displaystyle \nonumber\end{eqnarray}$$Thus,
$$\begin{eqnarray}\displaystyle \tilde{d} & = & \displaystyle -c_{1}+\frac{2c-2\sqrt{c}\sqrt{c-c_{1}u_{0}+c_{2}u_{0}^{2}}}{u_{0}}\nonumber\\ \displaystyle & = & \displaystyle -c-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}+\frac{2c-2y\sqrt{c}F(0,y)}{1-y^{2}}.\square\nonumber\end{eqnarray}$$Remark 4.3. Let
$$\begin{eqnarray}h:z\mapsto \frac{4z}{(1+z)^{2}}.\end{eqnarray}$$ This is an analytic one-to-one map from the open unit disc 
$\mathbb{D}$ onto the cut plane 
$z\in \mathbb{C}\setminus [1,\infty [$ (see, e.g., [Reference Demni and Hamdi6]). Its inverse is given by:
$$\begin{eqnarray}h^{-1}(z)=\frac{1-\sqrt{1-z}}{1+\sqrt{1-z}}=\frac{z}{(1+\sqrt{1-z})^{2}},\end{eqnarray}$$ where the principal branch of the square root is taken. Then, the flow 
$\unicode[STIX]{x1D719}_{t}$ rewrites as 
$\unicode[STIX]{x1D719}_{t}(z)=-h^{-1}(u_{t}(z))$, for real values of 
$z\in \unicode[STIX]{x1D6FA}_{t}$, where
$$\begin{eqnarray}\displaystyle u_{t}(z)=\frac{4cde^{t\sqrt{c}}}{(c_{1}+de^{t\sqrt{c}})^{2}-4cb^{2}}. & & \displaystyle \nonumber\end{eqnarray}$$Remark 4.4. From 
$u_{t}(z)=h(-\unicode[STIX]{x1D719}_{t}(z))$, one easily sees, by analytic continuation, that 
$u_{t}$ is one-to-one from 
$\unicode[STIX]{x1D6FA}_{t}$ onto 
$\mathbb{C}\setminus [1,\infty [$. In particular, the identity 
$u_{t}(\unicode[STIX]{x1D702}_{t}(z))=h(-z)$ holds for any 
$z\in \mathbb{D}$. Moreover, from Proposition 4.2, we have
$$\begin{eqnarray}\displaystyle d(z)=-c(z)-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}+2c(z)\frac{H(0,z)^{2}+b^{2}-a^{2}\left({\displaystyle \frac{1-z}{1+z}}\right)^{2}}{c(z)+{\displaystyle \frac{1+z}{1-z}}\sqrt{c(z)}H(0,z)}. & & \displaystyle \nonumber\end{eqnarray}$$ Since 
$c(z)$ is an analytic function in 
$\mathbb{D}$ (with values in 
$\mathbb{C}\setminus ]\infty ,0]$) and since
$$\begin{eqnarray}\displaystyle z\mapsto c(z)+\frac{1+z}{1-z}\sqrt{c(z)}H(0,z) & & \displaystyle \nonumber\end{eqnarray}$$ does not vanish in the closed unit disc, we deduce that 
$d(z)$ is analytic on 
$\mathbb{D}$ and therefore the function 
$u_{t}(z)$ is meromorphic on 
$\mathbb{D}$.
5 Consequences
In this section, we derive some consequences of our preceding results on the regularity of the boundary of 
$\unicode[STIX]{x1D6FA}_{t}=\unicode[STIX]{x1D702}_{t}(\mathbb{D})$ and the spectra of 
$RU_{t}SU_{t}^{\ast }$. Observe from the equality 
$\unicode[STIX]{x1D702}_{t}(\overline{z})=\overline{\unicode[STIX]{x1D702}_{t}(z)}$ that 
$\unicode[STIX]{x1D6FA}_{t}$ is symmetric with respect to the real axis. Denote by 
$\mathbb{D}^{+}$ and 
$\mathbb{D}^{-}$ the upper and lower parts of 
$\mathbb{D}$ and let 
$\tilde{h}$ be the restriction of 
$h$ to the region 
$\mathbb{D}^{+}\cup (-1,1)$. Then, 
$\tilde{h}$ has a one-to-one continuation to the boundary 
$\unicode[STIX]{x2202}\mathbb{T}^{+}\cup \{\pm 1\}$ onto 
$[1,\infty ]$. Henceforth, we shall keep the same notation 
$\tilde{h}$ for the continuous extension of the restriction of 
$h$ to 
$\mathbb{D}^{+}\cup (-1,1)$. Set
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{t}(z)=\left\{\begin{array}{@{}ll@{}}-\tilde{h}^{-1}(u_{t}(z)),\quad & z\in \mathbb{D}^{+}\cup (-1,1)\\ -\overline{\tilde{h}^{-1}(u_{t}(\overline{z}))},\quad & z\in \mathbb{D}^{-}.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$ From Remark 4.4, this function is meromorphic on 
$\mathbb{D}$ and its restriction to 
$\unicode[STIX]{x1D6FA}_{t}$ coincides with the conformal map 
$\unicode[STIX]{x1D719}_{t}$. Let
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}_{t}:=\{z\in \mathbb{D},\unicode[STIX]{x1D6F7}_{t}(z)\in \mathbb{D}\}=\{z\in \mathbb{D},u_{t}(z)\in \mathbb{C}\setminus [1,\infty [\,\} & & \displaystyle \nonumber\end{eqnarray}$$ be the analyticity region of 
$\unicode[STIX]{x1D6F7}_{t}$. Then, the region 
$\unicode[STIX]{x1D6FA}_{t}$ coincides with the connected component of 
$\unicode[STIX]{x1D6F4}_{t}$ containing the origin 
$z=0$. The ODE (4.7) can easily be transformed into
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6F7}_{t}(z)=\unicode[STIX]{x1D6F7}_{t}(z)H(t,\unicode[STIX]{x1D6F7}_{t}(z)),\quad \unicode[STIX]{x1D6F7}_{0}(z)=z.\end{eqnarray}$$ Which is nothing less than the ODE (4.3) (the radial Loewner ODE driven by 
$\unicode[STIX]{x1D708}_{t}$). Moreover, it holds for any 
$z\in \unicode[STIX]{x1D6F4}_{t}$. The next proposition proves that the inverse 
$\unicode[STIX]{x1D702}_{t}$ of the restriction of 
$\unicode[STIX]{x1D6F7}_{t}$ to 
$\unicode[STIX]{x1D6FA}_{t}$ extends continuously to the boundary 
$\unicode[STIX]{x2202}\mathbb{D}$.
(1)
$\unicode[STIX]{x1D702}_{t}$ extends continuously to $\unicode[STIX]{x2202}\mathbb{D}$ and $\unicode[STIX]{x1D702}_{t}$ is one-to-one on $\overline{\mathbb{D}}$.(2)
$\unicode[STIX]{x1D6FA}_{t}$ is a simply connected domain bounded by a simple closed curve.
Proof. Since 
$\unicode[STIX]{x1D702}_{t}$ is a conformal map with image 
$\unicode[STIX]{x1D6FA}_{t}$, and its inverse is the restriction of 
$\unicode[STIX]{x1D6F7}_{t}$ to 
$\unicode[STIX]{x1D6FA}_{t}$ then, it suffices to prove that the function 
$\unicode[STIX]{x1D6F7}_{t}$ satisfies the properties in [Reference Belinschi and Bercovici1, Theorem 4.4]. It is not difficult to see that 
$\unicode[STIX]{x1D6F7}_{t}(0)=\unicode[STIX]{x1D719}_{t}(0)=0$. Moreover, for any 
$z\in \unicode[STIX]{x1D6F4}_{t}$, we have
$$\begin{eqnarray}|\unicode[STIX]{x1D6F7}_{t}(z)|=|z|\exp \left(\int _{0}^{t}\Re H(s,\unicode[STIX]{x1D6F7}_{s}(z))ds\right)\geqslant |z|,\end{eqnarray}$$ where the equality follows from the integration of the ODE (5.1) and the inequality is due to the fact that 
$\Re H>0$. Otherwise (i.e., if 
$z$ is in the complementary set of 
$\unicode[STIX]{x1D6F4}_{t}$ in 
$\mathbb{D}$), we have 
$u_{t}(z)\in [1,\infty [$. It follows that, 
$\tilde{h}^{-1}(u_{t}(z))\in \mathbb{T}$ and then 
$|\unicode[STIX]{x1D6F7}_{t}(z)|=1>|z|$. Consequently, 
$|\unicode[STIX]{x1D6F7}_{t}(z)|\geqslant |z|$ for any 
$z\in \mathbb{D}$, and therefore assertions (1) and (2) follow immediately from [Reference Belinschi and Bercovici1, Theorem 4.4 and Proposition 4.5].◻
The following lemma shows that the boundary of 
$\unicode[STIX]{x1D6FA}_{t}$ is at a positive distance from 
$\pm 1$.
Lemma 5.2. The region 
$\overline{\unicode[STIX]{x1D6FA}_{t}}$ does not contain 1 (resp. 
$-1$) whenever 
$b>0$ or 
$b=0$ and 
$\unicode[STIX]{x1D708}_{0}\{0\}>0$ (resp. 
$a>0$ or 
$a=0$ and 
$\unicode[STIX]{x1D708}_{0}\{\unicode[STIX]{x1D70B}\}>0$).
Proof. Since 
$\unicode[STIX]{x1D708}_{0}\{0\}\geqslant b$ (see Corollary 3.7), by the assumption 
$b>0$ or 
$b=0$ and 
$\unicode[STIX]{x1D708}_{0}\{0\}>0$ we deduce that
$$\begin{eqnarray}\displaystyle \lim _{y\rightarrow +\infty }c(y) & = & \displaystyle \lim _{y\rightarrow +\infty }\left[F(0,y)-by-\frac{a}{y}\right]\left[F(0,y)+by+\frac{a}{y}\right]+\max \{\unicode[STIX]{x1D6FC}^{2},\unicode[STIX]{x1D6FD}^{2}\}\nonumber\\ \displaystyle & = & \displaystyle +\infty .\nonumber\end{eqnarray}$$Moreover, from the equality (see Proposition 4.2)
$$\begin{eqnarray}\displaystyle d(y)=c(y)\left[-1-\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{c(y)}+\frac{2}{1-y^{2}}+2\sqrt{\frac{1}{(y^{2}-1)^{2}}+\frac{c(y)+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{c(y)(y^{2}-1)}+\frac{b^{2}}{c(y)}}\right], & & \displaystyle \nonumber\end{eqnarray}$$we see that,
$$\begin{eqnarray}\displaystyle \lim _{y\rightarrow +\infty }d(y)=-\infty \qquad \text{and}\qquad \lim _{y\rightarrow +\infty }\frac{d(y)}{c(y)}=-1. & & \displaystyle \nonumber\end{eqnarray}$$As a result,
$$\begin{eqnarray}\displaystyle w_{t}(y)=\sqrt{\frac{\left(b^{2}-a^{2}-c(y)+d(y)e^{t\sqrt{c(y)}}\right)^{2}-4a^{2}c(y)}{\left(b^{2}-a^{2}+c(y)+d(y)e^{t\sqrt{c(y)}}\right)^{2}-4b^{2}c(y)}} & & \displaystyle \nonumber\end{eqnarray}$$ converges to 1 when 
$y$ goes to 
$+\infty$. Equivalently, in the 
$z$-variable we have, 
$\lim _{z\rightarrow 1^{-}}\unicode[STIX]{x1D719}_{t}(z)=0$ (see Proposition 4.2). Proceeding in the same way, we prove that 
$\lim _{z\rightarrow -1^{+}}\unicode[STIX]{x1D719}_{t}(z)=0$. Note that, in this case, 
$\unicode[STIX]{x1D708}_{0}\{\unicode[STIX]{x1D70B}\}\geqslant a$ and the assumption 
$a>0$ or 
$a=0$ and 
$\unicode[STIX]{x1D708}_{0}\{\unicode[STIX]{x1D70B}\}>0$ implies that 
$\lim _{y\rightarrow 0}c(y)=+\infty$ and 
$\lim _{y\rightarrow 0}d(y)/c(y)=1$. Since 
$\unicode[STIX]{x1D719}_{t}(0)=0$ and 
$\unicode[STIX]{x1D6FA}_{t}$ is a simply connected domain bounded by a simple closed curve, we see that 
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{t}$ intersect 
$x$-axis at two points 
$x(t)_{\pm }$ from either side of the origin, with 
$\unicode[STIX]{x1D719}_{t}(x(t)_{\pm })=\pm 1$. From 
$\lim _{z\rightarrow \pm 1^{\mp }}\unicode[STIX]{x1D719}_{t}(z)=0$, we deduce that 
$[x(t)_{-},x(t)_{+}]\subset (-1,1)$.◻
Corollary 5.3. For any 
$t>0$,
$$\begin{eqnarray}\displaystyle z\mapsto a\frac{1-\unicode[STIX]{x1D702}_{t}(z)}{1+\unicode[STIX]{x1D702}_{t}(z)}+b\frac{1+\unicode[STIX]{x1D702}_{t}(z)}{1-\unicode[STIX]{x1D702}_{t}(z)} & & \displaystyle \nonumber\end{eqnarray}$$ is a function of Hardy class 
$H^{\infty }(\mathbb{D})$.
Proof. By the first item of Proposition 5.1, we can easily confirm that 
$\unicode[STIX]{x1D702}_{t}$ is of hardy class 
$H^{\infty }(\mathbb{D})$ and hence the function
$$\begin{eqnarray}\displaystyle z\mapsto a\frac{1-\unicode[STIX]{x1D702}_{t}(z)}{1+\unicode[STIX]{x1D702}_{t}(z)}+b\frac{1+\unicode[STIX]{x1D702}_{t}(z)}{1-\unicode[STIX]{x1D702}_{t}(z)} & & \displaystyle \nonumber\end{eqnarray}$$ is of hardy class 
$H^{\infty }(\mathbb{D})$ by the previous Lemma, thanks to the fact that 
$\unicode[STIX]{x1D702}_{t}$ cannot take the values 
$\pm 1$ in 
$\mathbb{D}$.◻
We close this paragraph with the following result on the spectra of 
$RU_{t}SU_{t}^{\ast }$.
Proposition 5.4. For every 
$t>0$, 0 and 
$\unicode[STIX]{x1D70B}$ does not belong to the continuous singular spectrum of 
$\unicode[STIX]{x1D70E}_{t}$.
Proof. By the second item in Proposition 5.1 and the subordination relation (4.2), the function 
$K(t,.)$ has an analytic continuation in some neighborhoods of 
$\pm 1$ and
$$\begin{eqnarray}\displaystyle \lim _{z\rightarrow \pm 1^{\mp }}K(t,z)=\lim _{z\rightarrow \pm 1^{\mp }}K(0,\unicode[STIX]{x1D702}_{t}(z))=K(0,x(t)_{\pm }), & & \displaystyle \nonumber\end{eqnarray}$$ where 
$x(t)_{\pm }$ are the real boundaries of 
$\unicode[STIX]{x1D6FA}_{t}$ (see the proof of Lemma 5.2). Let 
$L(t,z)$ be as in Corollary 3.5, and rewrite (4.1) as
$$\begin{eqnarray}\displaystyle K(t,z)^{2}=4L(t,z)\left(L(t,z)+a\frac{1-z}{1+z}+b\frac{1+z}{1-z}\right). & & \displaystyle \nonumber\end{eqnarray}$$Then, we have
$$\begin{eqnarray}\displaystyle K(0,x(t)_{\pm })^{2}=4\lim _{z\rightarrow \pm 1^{\mp }}L(t,z)\left(L(t,z)+a\frac{1-z}{1+z}+b\frac{1+z}{1-z}\right). & & \displaystyle \nonumber\end{eqnarray}$$Since
$$\begin{eqnarray}\displaystyle L(t,z)+a\frac{1-z}{1+z}+b\frac{1+z}{1-z} & & \displaystyle \nonumber\end{eqnarray}$$ blows up as 
$z\rightarrow \pm 1^{\mp }$, we deduce that 
$\lim _{z\rightarrow \pm 1^{\mp }}L(t,z)=0$. Consequently, the Poisson transform of 
$\unicode[STIX]{x1D70E}_{t}$, which is nothing but the real part of 
$L(t,z)$, vanishes as 
$z\rightarrow \pm 1^{\mp }$ and hence the desired assertion follows from Proposition 1.3.11 and equation (1.8.8) in [Reference Cima, Matheson and Ross3].◻
6 Free mutual information and orbital free entropy
Here is our main application to the proof of the conjecture 
$i^{\ast }=-\unicode[STIX]{x1D712}_{\text{orb}}$. For a pair of projections 
$(P,Q)$, we use the same definitions of the free mutual information 
$i^{\ast }(\mathbb{C}P+\mathbb{C}(I-P);\mathbb{C}Q+\mathbb{C}(I-Q))$ (hereafter 
$i^{\ast }(P:Q)$) and the orbital free entropy 
$\unicode[STIX]{x1D712}_{\text{orb}}(P,Q)$ as expounded in the last section of the paper [Reference Izumi and Ueda15]. We refer the reader to [Reference Hiai and Petz13, Reference Hiai and Ueda14, Reference Voiculescu19] for more information. Using subordination technology, a partial result for the identity 
$i^{\ast }(P:Q)=-\unicode[STIX]{x1D712}_{\text{orb}}(P,Q)$ is obtained in [Reference Izumi and Ueda15, Lemma 4.4] (note that the function 
$H$ there is exactly our 
$\frac{1}{4}K^{2}$). The result is as follows.
Lemma 6.1. [Reference Izumi and Ueda15]
If 
$K(t,.)$ define a function of Hardy class 
$H^{3}(\mathbb{D})$ for any 
$t>0$, then 
$i^{\ast }\left(\mathbb{C}P+\mathbb{C}(I-P);\mathbb{C}Q+\mathbb{C}(I-Q)\right)=-\unicode[STIX]{x1D712}_{\text{orb}}(P,Q)$.
From
$$\begin{eqnarray}\displaystyle 4(\Re L(t,z))^{2}\leqslant 4\Re L(t,z)\Re \left(L(t,z)+a\frac{1-z}{1+z}+b\frac{1+z}{1-z}\right)\leqslant |K(t,z)|^{2}, & & \displaystyle \nonumber\end{eqnarray}$$ the assumption in Lemma 6.1 implies that 
$\unicode[STIX]{x1D70E}_{t}$ has an 
$L^{3}$-density. The converse remains true; that is, if 
$\unicode[STIX]{x1D70E}_{t}$ has an 
$L^{3}$-density for any 
$t>0$, then 
$K(t,.)$ becomes a function of Hardy class 
$H^{3}(\mathbb{D})$. In fact, according to [Reference Conway5, Theorem 1.7, p. 208], 
$L(t,.)$ is a function of Hardy class 
$H^{3}(\mathbb{D})$. On the other hand, from Corollary 3.7 and Proposition 5.4, we see that 
$L(t,.)$ has an analytic continuation across both points 
$\pm 1$. Moreover, the limit 
$\lim _{z\rightarrow \pm 1}L(t,z)=0$ implies that the constant term in the power series expansion around 
$z=\pm 1$ is zero. So that 
$L(t,z)(a((1-z)/(1+z))+b((1+z)/(1-z)))$ is bounded in some neighborhoods at both 
$\pm 1$. Hence
$$\begin{eqnarray}\displaystyle K(t,z)^{2}=4L(t,z)^{2}+4L(t,z)\left(a\frac{1-z}{1+z}+b\frac{1+z}{1-z}\right) & & \displaystyle \nonumber\end{eqnarray}$$ becomes a function of Hardy class 
$H^{3/2}(\mathbb{D})$. From these discussions, we deduce that
Lemma 6.2. If 
$\unicode[STIX]{x1D70E}_{t}$ has an 
$L^{3}$-density for every 
$t>0$, then 
$i^{\ast }(P:Q)=-\unicode[STIX]{x1D712}_{\text{orb}}(P,Q)$.
Here we reprove the same result by an equivalent but more handy assumption.
Proposition 6.3. Assume that for every 
$t>0$, 
$H(0,\unicode[STIX]{x1D702}_{t}(.))$ is a function of Hardy class 
$H^{3}(\mathbb{D})$. Then the equality 
$i^{\ast }(P:Q)=-\unicode[STIX]{x1D712}_{\text{orb}}(P,Q)$ holds.
Proof. We will prove that the assumptions 
$H(0,\unicode[STIX]{x1D702}_{t}(.))\in H^{3}(\mathbb{D})$ and 
$K(t,.)\in H^{3}(\mathbb{D})$ are equivalent and so we can use the result of Lemma 6.1. To this end, we use the subordination relation (4.2) to rewrite (4.1) as
$$\begin{eqnarray}\displaystyle K(t,z)^{2}=H(0,\unicode[STIX]{x1D702}_{t}(z))^{2}-\left(a\frac{1-\unicode[STIX]{x1D702}_{t}(z)}{1+\unicode[STIX]{x1D702}_{t}(z)}+b\frac{1+\unicode[STIX]{x1D702}_{t}(z)}{1-\unicode[STIX]{x1D702}_{t}(z)}\right)^{2}. & & \displaystyle \nonumber\end{eqnarray}$$But, the function (see Corollary 5.3)
$$\begin{eqnarray}\displaystyle z\mapsto \left(a\frac{1-\unicode[STIX]{x1D702}_{t}(z)}{1+\unicode[STIX]{x1D702}_{t}(z)}+b\frac{1+\unicode[STIX]{x1D702}_{t}(z)}{1-\unicode[STIX]{x1D702}_{t}(z)}\right)^{2} & & \displaystyle \nonumber\end{eqnarray}$$ is of hardy class 
$H^{\infty }(\mathbb{D})$. Hence we are done.◻
Here is a sample application of Proposition 6.3 improving the result in [Reference Izumi and Ueda15, Corollary 4.5].
Lemma 6.4. Assume that 
$\unicode[STIX]{x1D70E}_{0}$ has an 
$L^{3}$-density with respect to 
$d\unicode[STIX]{x1D703}$. Then 
$i^{\ast }(P:Q)=-\unicode[STIX]{x1D712}_{\text{orb}}(P,Q)$.
Proof. Under the assumption here and according to [Reference Conway5, Theorem 1.7, p. 208], 
$L(0,z)$ is a function of Hardy class 
$H^{3}(\mathbb{D})$ and hence so does 
$L(0,\unicode[STIX]{x1D702}_{t}(z))$ too by Littlewood’s subordination theorem (see [Reference Duren9, Theorem 1.7]). Hence, by Corollary 5.3, the function
$$\begin{eqnarray}\displaystyle H(0,\unicode[STIX]{x1D702}_{t}(z))=2L(0,\unicode[STIX]{x1D702}_{t}(z))+a\frac{1-\unicode[STIX]{x1D702}_{t}(z)}{1+\unicode[STIX]{x1D702}_{t}(z)}+b\frac{1+\unicode[STIX]{x1D702}_{t}(z)}{1-\unicode[STIX]{x1D702}_{t}(z)} & & \displaystyle \nonumber\end{eqnarray}$$ is of hardy class 
$H^{3}(\mathbb{D})$ and then we are done thanks to Proposition 6.3.◻
We can now prove the main result of this section.
Theorem 6.5. For any two projections 
$P,Q$, if
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{t}-(1-\min \{\unicode[STIX]{x1D70F}(P),\unicode[STIX]{x1D70F}(Q)\})\unicode[STIX]{x1D6FF}_{0}-\max \{\unicode[STIX]{x1D70F}(P)+\unicode[STIX]{x1D70F}(Q)-1,0\}\unicode[STIX]{x1D6FF}_{1} & & \displaystyle \nonumber\end{eqnarray}$$ has an 
$L^{3}$-density with respect to 
$x(1-x)\,dx$ on 
$[0,1]$ for 
$t=0$ or every 
$t>0$, then 
$i^{\ast }(P:Q)=-\unicode[STIX]{x1D712}_{\text{orb}}(P,Q)$.
Proof. From the relationship 
$\unicode[STIX]{x1D707}_{t}\leftrightsquigarrow \unicode[STIX]{x1D708}_{t}$ and the assumption here (together with Remark 3.4), we deduce that
$$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D707}_{t}}-(1-\min \{\unicode[STIX]{x1D70F}(P),\unicode[STIX]{x1D70F}(Q)\})\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}}-\max \{\unicode[STIX]{x1D70F}(P)+\unicode[STIX]{x1D70F}(Q)-1,0\}\unicode[STIX]{x1D6FF}_{0} & & \displaystyle \nonumber\end{eqnarray}$$ has an 
$L^{3}$-density with respect to 
$d\unicode[STIX]{x1D703}$ on 
$\mathbb{T}=(-\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}]$ for 
$t=0$ or every 
$t>0$ and hence by (3.5), the measure 
$\unicode[STIX]{x1D70E}_{t}$ does so also. The desired identity immediately follows from Lemmas 6.2 and 6.4.◻
