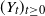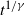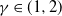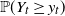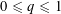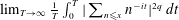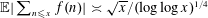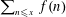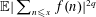Refine search
Actions for selected content:
72 results
Inverse clustering of Gibbs partitions via independent fragmentation and dual dependent coagulation operators
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 30 July 2025, pp. 1-18
-
- Article
- Export citation
Extremal behavior of stationary marked point processes
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 18 June 2025, pp. 1-42
-
- Article
- Export citation
Some conditional properties of superprocesses in random environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 08 April 2025, pp. 1156-1172
- Print publication:
- September 2025
-
- Article
- Export citation
Gaussian approximation and moderate deviations of Poisson shot noises with application to compound generalized Hawkes processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 305-345
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotics of the allele frequency spectrum and the number of alleles
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 516-540
- Print publication:
- June 2025
-
- Article
- Export citation
Weak convergence of the extremes of branching Lévy processes with regularly varying tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 December 2023, pp. 622-643
- Print publication:
- June 2024
-
- Article
- Export citation
Adaptation of a population to a changing environment in the light of quasi-stationarity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 235-286
- Print publication:
- March 2024
-
- Article
- Export citation
Large deviations of Poisson Telecom processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 12 October 2022, pp. 267-283
- Print publication:
- March 2023
-
- Article
- Export citation
On strongly rigid hyperfluctuating random measures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 August 2022, pp. 948-961
- Print publication:
- December 2022
-
- Article
- Export citation
A generalised Dickman distribution and the number of species in a negative binomial process model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 370-399
- Print publication:
- June 2021
-
- Article
- Export citation
An elementary derivation of moments of Hawkes processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 102-137
- Print publication:
- March 2020
-
- Article
- Export citation
MOMENTS OF RANDOM MULTIPLICATIVE FUNCTIONS, I: LOW MOMENTS, BETTER THAN SQUAREROOT CANCELLATION, AND CRITICAL MULTIPLICATIVE CHAOS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 January 2020, e1
-
- Article
-
- You have access
- Open access
- Export citation
Percolation results for the continuum random cluster model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 231-244
- Print publication:
- March 2018
-
- Article
- Export citation
Asymptotics for randomly reinforced urns with random barriers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1206-1220
- Print publication:
- December 2016
-
- Article
- Export citation
Laplace transform identities for the volume of stopping sets based on Poisson point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 919-933
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Admission Control for Multidimensional Workload input with Heavy Tails and Fractional Ornstein-Uhlenbeck Process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 476-505
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Statistics for Poisson Models of Overlapping Spheres
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 937-962
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Modelling Electricity Futures by Ambit Fields
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 719-745
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Limit Theorems for Continuous-Time Branching Flows
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 317-332
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Species Dynamics in the Two-Parameter Poisson-Dirichlet Diffusion Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 174-190
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation