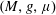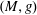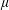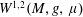Refine search
Actions for selected content:
13 results
Towards Riemannian diffeology
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 December 2025, pp. 1-30
-
- Article
- Export citation
On a general matrix-valued unbalanced optimal transport problem
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1063-1095
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of flat holonomies
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1048-1077
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimization of the anisotropic Cheeger constant with respect to the anisotropy
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 1030-1043
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE RESOLVENT AND RIESZ TRANSFORM ON CONNECTED SUMS OF MANIFOLDS WITH DIFFERENT ASYMPTOTIC DIMENSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 24 June 2021, pp. 344-345
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
Metrizability of Holonomy Invariant Projective Deformation of Sprays
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 23 January 2020, pp. 701-714
- Print publication:
- September 2023
-
- Article
- Export citation
ON THE PROBLEM OF NON-BERWALDIAN LANDSBERG SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 331-341
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Infinitesimal Hilbertianity of Weighted Riemannian Manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 118-140
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
On a Yamabe Type Problem in Finsler Geometry
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 2 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 253-268
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
A Second Order Smooth Variational Principle on Riemannian Manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 2 / 01 April 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-260
- Print publication:
- 01 April 2010
-
- Article
-
- You have access
- Export citation
An Algebraic Approach to Weakly Symmetric Finsler Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 52-73
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
Singularities of centre symmetry sets
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 90 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 16 December 2004, pp. 132-166
- Print publication:
- January 2005
-
- Article
- Export citation
A Symplectic Approach to Yang Mills Theory for Non Commutative Tori
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 2 / 01 April 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 368-387
- Print publication:
- 01 April 1992
-
- Article
-
- You have access
- Export citation