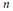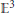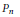Refine search
Actions for selected content:
7 results
GAUSSIAN HOLOMORPHIC SECTIONS ON NONCOMPACT COMPLEX MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1197-1262
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformation of Dirac operators along orbits and quantization of noncompact Hamiltonian torus manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 09 March 2021, pp. 1062-1092
- Print publication:
- August 2022
-
- Article
- Export citation
SUPERORBITS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 20 July 2016, pp. 1065-1120
- Print publication:
- November 2018
-
- Article
- Export citation
Complex submanifolds, connections and asymptotics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 373-383
-
- Article
-
- You have access
- Export citation
THE DIRECT INTEGRAL OF SOME WEIGHTED BERGMAN SPACES
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 50 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 February 2007, pp. 115-122
-
- Article
-
- You have access
- Export citation
SYMPLECTIC FOUR-MANIFOLDS AND CONFORMAL BLOCKS
-
- Journal:
- Journal of the London Mathematical Society / Volume 71 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 06 April 2005, pp. 503-515
- Print publication:
- April 2005
-
- Article
- Export citation
Quantization of Bending Deformations of Polygons In
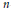 , Hypergeometric Integrals and the Gassner Representation
, Hypergeometric Integrals and the Gassner Representation
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 1 / 01 March 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 36-60
- Print publication:
- 01 March 2001
-
- Article
-
- You have access
- Export citation







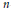 , Hypergeometric Integrals and the Gassner Representation
, Hypergeometric Integrals and the Gassner Representation