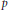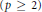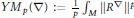Refine search
Actions for selected content:
10 results
CYT and SKT manifolds with parallel Bismut torsion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Calderon's problem for the connection Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 05 January 2024, pp. 1087-1112
- Print publication:
- June 2025
-
- Article
- Export citation
Nontame Morse–Smale flows and odd Chern–Weil theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 1579-1624
- Print publication:
- December 2022
-
- Article
- Export citation
ON 2-HOLONOMY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 September 2019, pp. 145-174
- Print publication:
- April 2021
-
- Article
- Export citation
Complex submanifolds, connections and asymptotics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 373-383
-
- Article
-
- You have access
- Export citation
Integrating
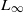 -algebras
-algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 1017-1045
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
On Gap Properties and Instabilities of p-Yang–Mills Fields
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 6 / 01 December 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1245-1259
- Print publication:
- 01 December 2007
-
- Article
-
- You have access
- Export citation
ON HOLOMORPHIC PRINCIPAL BUNDLES OVER A COMPACT RIEMANN SURFACE ADMITTING A FLAT CONNECTION, II
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 4 / July 2003
- Published online by Cambridge University Press:
- 09 June 2003, pp. 440-444
- Print publication:
- July 2003
-
- Article
- Export citation
An Inverse Problem in the Calculus of Variations and the Characteristic Curves of Connections on SO(3)-Bundles
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 2 / 01 June 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 129-140
- Print publication:
- 01 June 1995
-
- Article
-
- You have access
- Export citation
Certain Characteristics of the Curvature Tensor of an Affinely Connected Manifold
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 3 / 01 September 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 355-357
- Print publication:
- 01 September 1983
-
- Article
-
- You have access
- Export citation
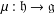
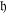
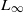 -algebras
-algebras