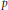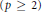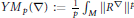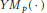Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dong, Yuxin
and
Wei, Shihshu Walter
2011.
On Vanishing Theorems for Vector Bundle Valued p-Forms and their Applications.
Communications in Mathematical Physics,
Vol. 304,
Issue. 2,
p.
329.
Jia, Gao-Yang
and
Zhou, Zhen-Rong
2013.
Stabilities of F-Yang-Mills fields on submanifolds.
Archivum Mathematicum,
p.
125.
Zhou, Zhen-Rong
2015.
Inequalities of Simons type and gaps for Yang–Mills fields.
Annals of Global Analysis and Geometry,
Vol. 48,
Issue. 3,
p.
223.
Zhou, Zhen-Rong
2016.
Energy gaps for Yang–Mills fields.
Journal of Mathematical Analysis and Applications,
Vol. 439,
Issue. 2,
p.
514.
Zhou, Zhen-Rong
2018.
Energy gaps for exponential Yang-Mills fields.
Archivum Mathematicum,
p.
127.
Baba, Kurando
and
Shintani, Kazuto
2025.
A Simons type condition for instability of F-Yang-Mills connections.
Differential Geometry and its Applications,
Vol. 100,
Issue. ,
p.
102275.