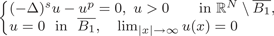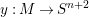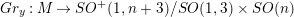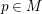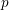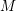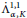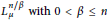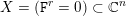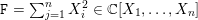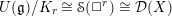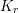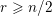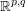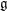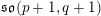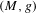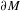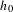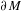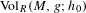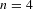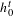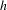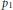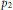Refine search
Actions for selected content:
16 results
Fast and slow decay solutions for supercritical fractional elliptic problems in exterior domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 28-53
- Print publication:
- February 2022
-
- Article
- Export citation
Surjective isometries of metric geometries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 828-839
- Print publication:
- December 2021
-
- Article
- Export citation
WEIERSTRASS–KENMOTSU REPRESENTATION OF WILLMORE SURFACES IN SPHERES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 35-59
- Print publication:
- December 2021
-
- Article
- Export citation
HOMOGENEOUS SASAKI AND VAISMAN MANIFOLDS OF UNIMODULAR LIE GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 08 November 2019, pp. 83-96
- Print publication:
- September 2021
-
- Article
- Export citation
Prescribed mean curvature equation on the unit ball in the presence of reflection or rotation symmetry
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 781-794
- Print publication:
- June 2019
-
- Article
- Export citation
Anisotropic Sobolev Capacity withFractional Order
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 4 / 01 August 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 873-889
- Print publication:
- 01 August 2017
-
- Article
-
- You have access
- Export citation
Higher symmetries of powers of the Laplacian and rings of differential operators
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 678-716
- Print publication:
- April 2017
-
- Article
- Export citation
THE RENORMALIZED VOLUME AND UNIFORMIZATION OF CONFORMAL STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 4 / September 2018
- Published online by Cambridge University Press:
- 30 June 2016, pp. 853-912
- Print publication:
- September 2018
-
- Article
- Export citation
Les applications conforme-harmoniques
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 2 / 01 April 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 266-298
- Print publication:
- 01 April 2013
-
- Article
-
- You have access
- Export citation
An Onofri-type Inequality on the Sphere with Two Conical Singularities
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 3 / 01 September 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 663-672
- Print publication:
- 01 September 2012
-
- Article
-
- You have access
- Export citation
PARA-BLASCHKE ISOPARAMETRIC HYPERSURFACES IN A UNIT SPHERE Sn + 1(1)*
-
- Journal:
- Glasgow Mathematical Journal / Volume 54 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 30 March 2012, pp. 579-597
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Regularity at space-like and null infinity
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-208
- Print publication:
- January 2009
-
- Article
- Export citation
CONFORMAL GEOMETRY OF THE (DISCRETE) SCHWARZIAN DAVEY-STEWARTSON II HIERARCHY
-
- Journal:
- Glasgow Mathematical Journal / Volume 47 / Issue A / June 2005
- Published online by Cambridge University Press:
- 14 July 2005, pp. 121-131
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Classification of Möbius Isoparametric Hypersurfaces in
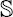 4
4
-
- Journal:
- Nagoya Mathematical Journal / Volume 179 / 2005
- Published online by Cambridge University Press:
- 11 January 2016, pp. 147-162
- Print publication:
- 2005
-
- Article
-
- You have access
- Export citation
Conformally flat hypersurfaces in Euclidean 4-space
-
- Journal:
- Nagoya Mathematical Journal / Volume 158 / December 2000
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-42
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
Conformally Flat Riemannian Manifolds as Hypersurfaces of the Light Cone
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 281-285
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation