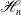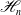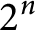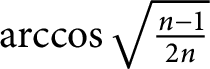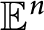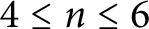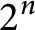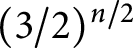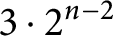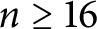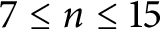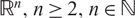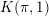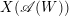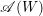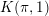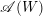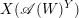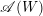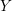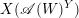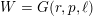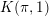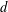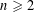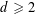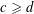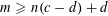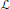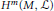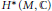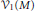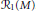Refine search
Actions for selected content:
27 results
On higher dimensional point sets in general position
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Forbidden induced subgraphs for graphs and signed graphs with eigenvalues bounded from below
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 01 October 2025, e163
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal Kinematics on
 $\mathcal{M}_{0,n}$
$\mathcal{M}_{0,n}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperpolygonal arrangements
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vines and MAT-labeled graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 20 December 2024, e128
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GV and GW invariants via the enhanced movable cone
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shi arrangements and low elements in affine Coxeter groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 12 February 2024, pp. 683-713
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stellahedral geometry of matroids
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 09 October 2023, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON 2-TRANSITIVE SETS OF EQUIANGULAR LINES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 22 August 2022, pp. 134-145
- Print publication:
- February 2023
-
- Article
- Export citation
Spherical coverings and X-raying convex bodies of constant width
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 860-866
- Print publication:
- December 2022
-
- Article
- Export citation
ON GILP’S GROUP-THEORETIC APPROACH TO FALCONER’S DISTANCE PROBLEM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 28 July 2020, pp. 547-562
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
THE MAGNETIC FIELD ABOUT A THREE-DIMENSIONAL BLOCK NEODYMIUM MAGNET
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 22 June 2020, pp. 386-405
-
- Article
-
- You have access
- Export citation
On the
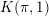 $K(\unicode[STIX]{x1D70B},1)$-problem for restrictions of complex reflection arrangements
$K(\unicode[STIX]{x1D70B},1)$-problem for restrictions of complex reflection arrangements
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 3 / March 2020
- Published online by Cambridge University Press:
- 20 January 2020, pp. 526-532
- Print publication:
- March 2020
-
- Article
- Export citation
Bisecting measures with hyperplane arrangements
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 3 / November 2020
- Published online by Cambridge University Press:
- 31 October 2019, pp. 639-647
- Print publication:
- November 2020
-
- Article
- Export citation
CUTTING A PART FROM MANY MEASURES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 17 October 2019, e37
-
- Article
-
- You have access
- Open access
- Export citation
Nearly free curves and arrangements: a vector bundle point of view
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 06 September 2019, pp. 51-74
- Print publication:
- January 2021
-
- Article
- Export citation
LOCAL NEGATIVITY OF SURFACES WITH NON-NEGATIVE KODAIRA DIMENSION AND TRANSVERSAL CONFIGURATIONS OF CURVES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 18 January 2019, pp. 123-135
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
ON VANISHING THEOREMS FOR LOCAL SYSTEMS ASSOCIATED TO LAURENT POLYNOMIALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 18 July 2017, pp. 1-22
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
Admissibility of Local Systems for some Classes of Line Arrangements
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 658-672
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
Hyperplane arrangements of Torelli type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 14 December 2012, pp. 309-332
- Print publication:
- February 2013
-
- Article
- Export citation