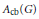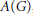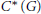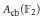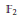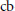Refine search
Actions for selected content:
19 results
A note on the column–row property
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1244-1254
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On quotient modules of H2(𝔻n): essential normality and boundary representations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 31 January 2019, pp. 1339-1359
- Print publication:
- June 2020
-
- Article
- Export citation
Fourier Spaces and Completely Isometric Representations of Arens Product Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 717-747
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
EMBEDDINGS AND
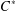 $C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
$C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 274-285
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
New Deformations of Convolution Algebras and Fourier Algebras on Locally Compact Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 2 / 01 April 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 434-452
- Print publication:
- 01 April 2017
-
- Article
-
- You have access
- Export citation
A SPECTRAL CHARACTERIZATION OF
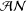 ${\mathcal{A}}{\mathcal{N}}$ OPERATORS
${\mathcal{A}}{\mathcal{N}}$ OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 369-391
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Categorical Aspects of Quantum Groups: Multipliers and Intrinsic Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 2 / 01 April 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 309-333
- Print publication:
- 01 April 2016
-
- Article
-
- You have access
- Export citation
THE NON-COMMUTATIVE KHINTCHINE INEQUALITIES FOR
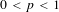 $0<p<1$
$0<p<1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 14 October 2015, pp. 1103-1123
- Print publication:
- November 2017
-
- Article
- Export citation
On Minimal and Maximal p-operator Space Structures
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 1 / 14 March 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 166-177
- Print publication:
- 14 March 2014
-
- Article
-
- You have access
- Export citation
Uniformly Continuous Functionals andM-Weakly Amenable Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 5 / 01 October 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1005-1019
- Print publication:
- 01 October 2013
-
- Article
-
- You have access
- Export citation
The Operator Space Projective Tensor Product: Embedding into the Second Dual and Ideal Structure
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 05 September 2013, pp. 505-519
-
- Article
-
- You have access
- Export citation
Norm One Idempotent cb-Multipliers with Applications to the Fourier Algebra in the cb-Multiplier Norm
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 4 / 01 December 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 654-662
- Print publication:
- 01 December 2011
-
- Article
-
- You have access
- Export citation
IDEALS IN OPERATOR SPACE PROJECTIVE TENSOR PRODUCT OF C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 18 November 2011, pp. 275-288
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
CO-REPRESENTATIONS OF HOPF–VON NEUMANN ALGEBRAS ON OPERATOR SPACES OTHER THAN COLUMN HILBERT SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 205-210
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
THE OPERATOR SHIFT SPACE
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 51 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 04 February 2008, pp. 229-263
-
- Article
-
- You have access
- Export citation
Operator Amenability of the Fourier Algebra in the cb-Multiplier Norm
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 5 / 01 October 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 966-980
- Print publication:
- 01 October 2007
-
- Article
-
- You have access
- Export citation
On the Ranges of Bimodule Projections
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 1 / 01 March 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 97-111
- Print publication:
- 01 March 2005
-
- Article
-
- You have access
- Export citation
THE OPERATOR HILBERT SPACE OH AND TYPE III VON NEUMANN ALGEBRAS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 4 / July 2004
- Published online by Cambridge University Press:
- 14 June 2004, pp. 455-459
- Print publication:
- July 2004
-
- Article
- Export citation
The Operator Amenability of Uniform Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 4 / 01 December 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 632-634
- Print publication:
- 01 December 2003
-
- Article
-
- You have access
- Export citation
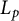
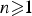
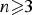

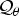

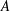
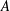
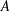
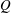
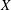
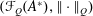
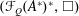
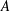

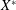
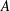
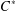
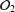
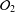
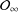
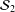
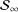
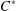
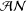
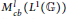
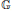

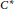
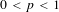
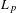
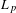
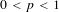
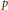

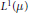

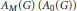
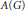
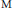
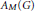
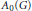
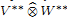 into
into 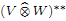 with a continuous inverse, where
with a continuous inverse, where 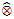 is the operator space projective tensor product. Further, for
is the operator space projective tensor product. Further, for 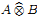 which, in particular, determines the lattice of closed ideals of
which, in particular, determines the lattice of closed ideals of 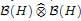 completely.
completely.
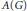
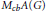
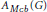
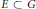

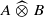 . As an application, a characterization of the prime ideals in the Banach *-algebra
. As an application, a characterization of the prime ideals in the Banach *-algebra 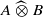 is obtained. In addition, we study the primitive ideals, modular ideals and the maximal modular ideals of
is obtained. In addition, we study the primitive ideals, modular ideals and the maximal modular ideals of 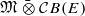 is a Banach algebra if and only if 𝔐 is subhomogeneous or
is a Banach algebra if and only if 𝔐 is subhomogeneous or