Article contents
The Operator Space Projective Tensor Product: Embedding into the Second Dual and Ideal Structure
Published online by Cambridge University Press: 05 September 2013
Abstract
We prove that, for operator spaces V and W, the operator space V** ⊗hW** can be completely isometrically embedded into (V ⊗hW)**, ⊗h being the Haagerup tensor product. We also show that, for exact operator spaces V and W, a jointly completely bounded bilinear form on V × W can be extended uniquely to a separately w*-continuous jointly completely bounded bilinear form on V× W**. This paves the way to obtaining a canonical embedding of 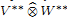 into
into  with a continuous inverse, where
with a continuous inverse, where 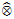 is the operator space projective tensor product. Further, for C*-algebras A and B, we study the (closed) ideal structure of
is the operator space projective tensor product. Further, for C*-algebras A and B, we study the (closed) ideal structure of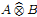 which, in particular, determines the lattice of closed ideals of
which, in particular, determines the lattice of closed ideals of 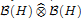 completely.
completely.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 2014
References
- 6
- Cited by

