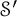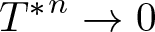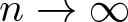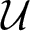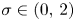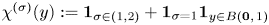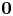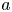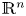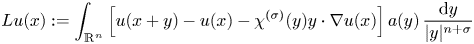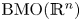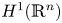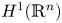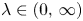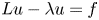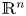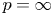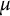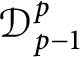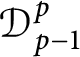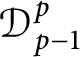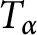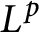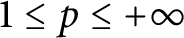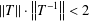Refine search
Actions for selected content:
87 results
Numerical range of Toeplitz and weighted composition operators on weighted Bergman spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 21 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An extension-restriction theorem for weighted Besov spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-48
-
- Article
- Export citation
Schatten class composition operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 883-890
- Print publication:
- September 2025
-
- Article
- Export citation
New aspects of Bargmann transform using Touchard polynomials and hypergeometric functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-46
-
- Article
- Export citation
Cesàro-type operators on Bergman–Morrey spaces and Dirichlet–Morrey spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 268-299
-
- Article
- Export citation
Minimal isometric dilations and operator models for the polydisc
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-40
-
- Article
- Export citation
A class of Hausdorff–Berezin operators on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 23 October 2024, pp. 1069-1080
- Print publication:
- December 2024
-
- Article
- Export citation
Characterization of continuous homomorphisms on entire slice monogenic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 17 May 2024, pp. 892-920
-
- Article
- Export citation
Growth of hypercyclic functions: a continuous path between
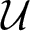 $\mathcal{U}$-frequent hypercyclicity and hypercyclicity
$\mathcal{U}$-frequent hypercyclicity and hypercyclicity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 08 May 2024, pp. 794-829
-
- Article
- Export citation
Dirichlet-type spaces of the unit bidisc and toral 2-isometries
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1271-1293
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On BMO and Hardy regularity estimates for a class of non-local elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 2025-2052
- Print publication:
- December 2023
-
- Article
- Export citation
On a class of Hilbert-type inequalities in the whole plane involving some classical kernel functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 06 October 2022, pp. 833-846
-
- Article
- Export citation
Volterra-type operators on the minimal Möbius-invariant space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 13 June 2022, pp. 509-524
- Print publication:
- June 2023
-
- Article
- Export citation
EXTREME POINT METHODS IN THE STUDY OF ISOMETRIES ON CERTAIN NONCOMMUTATIVE SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 06 August 2021, pp. 462-483
- Print publication:
- May 2022
-
- Article
- Export citation
Characterizations of Morrey type spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 328-344
- Print publication:
- June 2022
-
- Article
- Export citation
Multiplicities, invariant subspaces and an additive formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 279-297
-
- Article
- Export citation
WEIGHTED COMPOSITION OPERATORS BETWEEN LORENTZ SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 493-505
- Print publication:
- June 2021
-
- Article
- Export citation
Embedding of Dirichlet type spaces
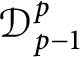 $\mathcal {D}^{p}_{p-1 }$ into tent spaces and Volterra operators
$\mathcal {D}^{p}_{p-1 }$ into tent spaces and Volterra operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 September 2020, pp. 697-708
- Print publication:
- September 2021
-
- Article
- Export citation
Growth of frequently hypercyclic functions for some weighted Taylor shifts on the unit disc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 264-281
- Print publication:
- June 2021
-
- Article
- Export citation
SMALL-BOUND ISOMORPHISMS OF FUNCTION SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 412-429
- Print publication:
- December 2021
-
- Article
- Export citation