Article contents
The Range of the Cesàro Operator Acting on 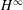 $H^{\infty }$
$H^{\infty }$
Published online by Cambridge University Press: 04 December 2019
Abstract
In 1993, N. Danikas and A. G. Siskakis showed that the Cesàro operator 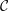 ${\mathcal{C}}$ is not bounded on
${\mathcal{C}}$ is not bounded on 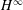 $H^{\infty }$; that is,
$H^{\infty }$; that is, 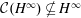 ${\mathcal{C}}(H^{\infty })\nsubseteq H^{\infty }$, but
${\mathcal{C}}(H^{\infty })\nsubseteq H^{\infty }$, but 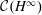 ${\mathcal{C}}(H^{\infty })$ is a subset of
${\mathcal{C}}(H^{\infty })$ is a subset of 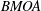 $BMOA$. In 1997, M. Essén and J. Xiao gave that
$BMOA$. In 1997, M. Essén and J. Xiao gave that 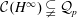 ${\mathcal{C}}(H^{\infty })\subsetneq {\mathcal{Q}}_{p}$ for every
${\mathcal{C}}(H^{\infty })\subsetneq {\mathcal{Q}}_{p}$ for every 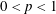 $0<p<1$. In this paper, we characterize positive Borel measures
$0<p<1$. In this paper, we characterize positive Borel measures 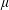 $\unicode[STIX]{x1D707}$ such that
$\unicode[STIX]{x1D707}$ such that 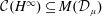 ${\mathcal{C}}(H^{\infty })\subseteq M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ and show that
${\mathcal{C}}(H^{\infty })\subseteq M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ and show that 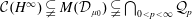 ${\mathcal{C}}(H^{\infty })\subsetneq M({\mathcal{D}}_{\unicode[STIX]{x1D707}_{0}})\subsetneq \bigcap _{0<p<\infty }{\mathcal{Q}}_{p}$ by constructing some measures
${\mathcal{C}}(H^{\infty })\subsetneq M({\mathcal{D}}_{\unicode[STIX]{x1D707}_{0}})\subsetneq \bigcap _{0<p<\infty }{\mathcal{Q}}_{p}$ by constructing some measures 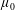 $\unicode[STIX]{x1D707}_{0}$. Here,
$\unicode[STIX]{x1D707}_{0}$. Here, 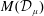 $M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ denotes the Möbius invariant function space generated by
$M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ denotes the Möbius invariant function space generated by 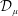 ${\mathcal{D}}_{\unicode[STIX]{x1D707}}$, where
${\mathcal{D}}_{\unicode[STIX]{x1D707}}$, where 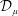 ${\mathcal{D}}_{\unicode[STIX]{x1D707}}$ is a Dirichlet space with superharmonic weight induced by a positive Borel measure
${\mathcal{D}}_{\unicode[STIX]{x1D707}}$ is a Dirichlet space with superharmonic weight induced by a positive Borel measure 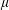 $\unicode[STIX]{x1D707}$ on the open unit disk. Our conclusions improve results mentioned above.
$\unicode[STIX]{x1D707}$ on the open unit disk. Our conclusions improve results mentioned above.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
The work was supported by NNSF of China (No. 11801347, No. 11720101003 and No. 11571217), NSF of Guangdong Province (No. 2018A030313512), Department of Education of Guangdong Province (No. 2017KQNCX078), Key projects of fundamental research in universities of Guangdong Province (No. 2018KZDXM034), and STU SRFT (No. NTF17020 and No. STF17005). F. Ye is the corresponding author.
References
- 8
- Cited by


