Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-10T22:29:11.399Z Has data issue: false hasContentIssue false
  • English
  • Français

New aspects of Bargmann transform using Touchard polynomials and hypergeometric functions

Part of: Special classes of linear operators Linear function spaces and their duals Spaces and algebras of analytic functions

Published online by Cambridge University Press:  09 January 2025

Daniel Alpay Open the ORCID record for Daniel Alpay [Opens in a new window] ,
Antonino De Martino  and
Kamal Diki Open the ORCID record for Kamal Diki [Opens in a new window]
Daniel Alpay
Affiliation:
Schmid College of Science and Technology, Chapman University, California 92866, USA e-mail: alpay@chapman.edu
Antonino De Martino*
Affiliation:
Politecnico di Milano, Dipartimento di Matematica, 20133 Milano, Italy
Kamal Diki
Affiliation:
Clifford research group, Department of Electronics and Information Systems, Faculty of Engineering and Architecture, Ghent University, 9000 Ghent, Belgium e-mail: Kamal.Diki@UGent.be
*
e-mail: antonino.demartino@polimi.it
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the ranges of the Schwartz space $\mathcal {S}$ and its dual 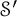$\mathcal {S}'$ (space of tempered distributions) under the Bargmann transform. The characterization of these two ranges leads to interesting reproducing kernel Hilbert spaces whose reproducing kernels can be expressed, respectively, in terms of the Touchard polynomials and the hypergeometric functions. We investigate the main properties of some associated operators and introduce two generalized Bargmann transforms in this framework. This can be considered as a continuation of an interesting research path that Neretin started earlier in his book on Gaussian integral operators.

Keywords

Bargmann transformTouchard polynomialshypergeometric functionsFock space

MSC classification

Primary: 30H20: Bergman spaces, Fock spaces 46E22: Hilbert spaces with reproducing kernels (=
Secondary: 47B38: Operators on function spaces (general)
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 46
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abreu, L. D., Sampling and interpolation in Bargmann–Fock spaces of polyanalytic functions . Appl. Comp. Harm. Anal. 29(2010), 287–302.CrossRefGoogle Scholar
Ali, S. T., Antoine, J. P., and Gazeau, J. P., Coherent states, wavelets and their generalizations. Vol. 3, Springer, New York, 2000.Google Scholar
Ali, S. T., Reproducing kernels in coherent states, wavelets, and quantization . In: D.Alpay (ed.), Operator theory, Springer, Basel, 2015, pp. 111–125.Google Scholar
Alpay, D., Cerejeiras, P., Kahler, U., and Kling, T., Commutators on Fock space . J. Math. Phys. 64(2023), no. 4, 21 pp.Google Scholar
Alpay, D., Colombo, F., Diki, K., and Sabadini, I., Reproducing kernel Hilbert spaces of polyanalytic functions of infinite order . Integr. Equ. Oper. Theory 94(2022), no. 4, 43 pp.Google Scholar
Alpay, D., Colombo, F., Diki, K., Sabadini, I., and Struppa, D. C., Superoscillations and Fock spaces . J. Math. Phys. 64(2023), no. 9, 20 pp.Google Scholar
Alpay, D., De Martino, A., Diki, K., and Struppa, D. C., Short-time Fourier transform (STFT) and superoscillations . Appl. Comput. Harmon. Anal. 73 (2024), Paper No. 101689, 31 pp.CrossRefGoogle Scholar
Bargmann, V., On a Hilbert space of analytic functions and an associated integral transform . Comm. Pure Appl. Math. 14(1961), 187–214.CrossRefGoogle Scholar
Bernstein, S. and Schufmann, S., The Segal–Bargmann transform in Clifford analysis . In: D. Alpay, R. Peretz, D. Shoikhet, M. B. Vajiac (eds.), New directions in function theory: From complex to hypercomplex to non-commutative, Chapman University, Birkhäuser, Cham, 2021, pp. 29–52.CrossRefGoogle Scholar
Colombo, F., Sabadini, I., and Sommen, F., On the Bargmann–Radon transform in the monogenic setting . J. Geom. Phys. 120(2017), 306–316 CrossRefGoogle Scholar
Cnudde, L. and De Bie, H., Slice Segal–Bargmann transform . J. Phys. A. 50(2017), no. 25, 23 pp.CrossRefGoogle Scholar
De Martino, A. and Diki, A. K., On the polyanalytic short-time Fourier transform in the quaternionic setting . Commun. Pure Appl. Anal. 21(2021), no. 11, 3629–3665.CrossRefGoogle Scholar
De Martino, A. and Diki, K., On the quaternionic short-time Fourier and Segal–Bargmann transforms . Mediterr. J. Math. 18(2021), no. 3, 22 pp.CrossRefGoogle Scholar
Diki, K. and Ghanmi, A., A quaternionic analogue of the Segal–Bargmann transform . Complex Anal. Oper. Theory 11(2017), 457–473.CrossRefGoogle Scholar
Diki, K., Krausshar, R. S., and Sabadini, I., On the Bargmann–Fock–Fueter and Bergman–Fueter integral transforms . J. Math. Phys. 60(2019), no. 8, 083506.CrossRefGoogle Scholar
Fu, Y., Li, L., Kaehler, U., and Cerejeiras, P., On the Fock space of metaanalytic functions . J. Math. Anal. Appl. 414(2014), no. 1, 176–187.CrossRefGoogle Scholar
Grothendieck, A., Topological vector spaces, Gordon and Breach, New York, 1973.Google Scholar
Hall, B. C., Quantum theory for mathematicians, Springer, New York, 2013.CrossRefGoogle Scholar
Hille, E., A class of reciprocal functions . Ann. Math. 27(1926), no. 4, 427–464.CrossRefGoogle Scholar
Knopf, P. M., The operator ${\left(z\frac{d}{dz}\right)}^n$ and its applications to series. Math. Mag 76(2003), no. 4, 364–371.CrossRefGoogle Scholar
Neretin, A. Y., Lectures on Gaussian integral operators and classic groups, Vol. 13, European Mathematical Society, Zurich, 2011.CrossRefGoogle Scholar
Pena Pena, D., Sabadini, I., and Sommen, F., Segal–Bargmann–Fock modules of monogenic functions . J. Math. Phy. 58(2017), 103507.CrossRefGoogle Scholar
Revus, D. and Yor, M., Continous martingales and Brownian motion, 3rd ed., Springer Verlag, 1999.CrossRefGoogle Scholar
Schmüdgen, K., The moment problem. Springer, New York, 2017.CrossRefGoogle Scholar
Schaefer, H., Topological vector spaces, Springer-Verlag, Berlin, 1986.Google Scholar
Szegö, G., Orthogonal polynomials, 4rd ed., American Mathematical Society, Providence, RI, 1975. American Mathematical Society, Colloquium Publications, Vol. XXIII.Google Scholar
Simon, B., Distributions and their Hermite expansions . J. Math. Phys. 12(1971), 140–148.CrossRefGoogle Scholar
Touchard, J., Sur les cycles des substitutions , Acta Math. 70(1939), no. 1, 243–297.CrossRefGoogle Scholar
van Eijndhoven, S. L. L. and Meyers, J. L. H., New orthogonality relations for the Hermite polynomials and related Hilbert spaces . J. Math. Ann. Appl. 146(1990), 89–98.CrossRefGoogle Scholar
Vasilevski, N. L., Poly-Fock spaces . In: V. M. Adamyan, I. Gohberg, M. Gorbachuk, V. Gorbachuk, M. A. Kaashoek, H. Langer, G. Popov (eds.), Differential operators and related topics: Proceedings of the Mark Krein international conference on operator theory and applications, Odessa, Ukraine, August 1822, 1997, Vol. I, Birkhäuser, Basel, 2000, pp. 371–386.CrossRefGoogle Scholar
Zhu, K., Analysis on Fock spaces, Graduate Texts in Mathematics, Vol. 263, Springer, Boston, MA, 2012.CrossRefGoogle Scholar