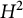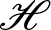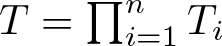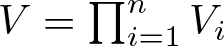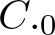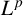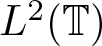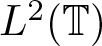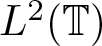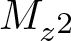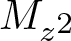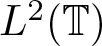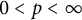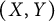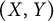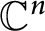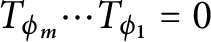Refine search
Actions for selected content:
63 results
A new asymptotic regime for the KdV equation with Wigner–von Neumann type initial data
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 20 November 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerical range of Toeplitz and weighted composition operators on weighted Bergman spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 21 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterization of numerical ranges for antilinear operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-16
-
- Article
- Export citation
A Cesàro-like operator from a class of analytic function spaces to analytic Besov spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1210-1222
- Print publication:
- December 2025
-
- Article
- Export citation
GAUSSIAN HOLOMORPHIC SECTIONS ON NONCOMPACT COMPLEX MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1197-1262
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE LINEAR COMBINATIONS OF MONOMIAL TOEPLITZ PRODUCTS ON THE BERGMAN SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 39-60
- Print publication:
- August 2025
-
- Article
- Export citation
On spectra of Hankel operators on the polydisc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 301-317
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Embedding of some classes of operators into strongly continuous semigroups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 219-231
- Print publication:
- March 2025
-
- Article
- Export citation
Hilbert type operators acting from the Bloch space into Bergman spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 205-225
-
- Article
- Export citation
Minimal isometric dilations and operator models for the polydisc
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-40
-
- Article
- Export citation
A note on the space of all Toeplitz operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 November 2024, pp. 1123-1140
- Print publication:
- December 2024
-
- Article
- Export citation
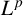 $L^p$-BOUNDEDNESS OF THE BEREZIN TRANSFORM ON GENERALISED HARTOGS TRIANGLES
$L^p$-BOUNDEDNESS OF THE BEREZIN TRANSFORM ON GENERALISED HARTOGS TRIANGLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 541-551
- Print publication:
- June 2025
-
- Article
- Export citation
Commutants and complex symmetry of finite Blaschke product multiplication operator in
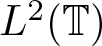 $L^2(\mathbb{T})$
$L^2(\mathbb{T})$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 261-286
-
- Article
- Export citation
Sub-Bergman Hilbert spaces on the unit disk III
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1520-1537
- Print publication:
- October 2024
-
- Article
- Export citation
Toeplitz determinants with a one-cut regular potential and Fisher–Hartwig singularities I. Equilibrium measure supported on the unit circle
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1431-1472
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Composition operators on weighted analytic spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 17 April 2023, pp. 1213-1230
- Print publication:
- December 2023
-
- Article
- Export citation
General Toeplitz kernels and
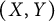 $(X,Y)$-invariance
$(X,Y)$-invariance
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 680-706
- Print publication:
- April 2024
-
- Article
- Export citation
Weighted composition operators on weighted Bergman and Dirichlet spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 28 April 2022, pp. 286-302
- Print publication:
- March 2023
-
- Article
- Export citation
Zero products of Toeplitz operators on Reinhardt domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 170-179
- Print publication:
- March 2022
-
- Article
- Export citation
Characterizations of Hankel operators in the essential commutant of quasicontinuous Toeplitz operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 44-51
- Print publication:
- March 2022
-
- Article
- Export citation