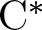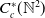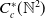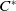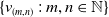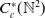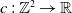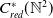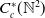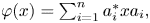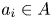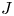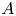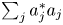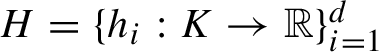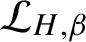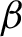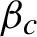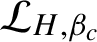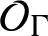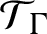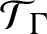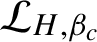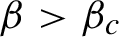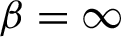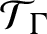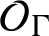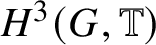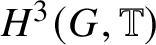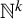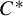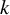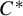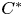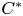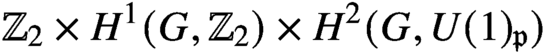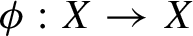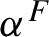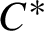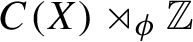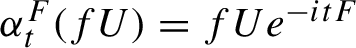Refine search
Actions for selected content:
24 results
Non-commutative skew-product extension dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2672-2694
- Print publication:
- September 2025
-
- Article
- Export citation
The admissible KMS bundles on classifiable C⁎-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tracial weights on topological graph algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 3428-3454
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KMS states on
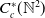 $C_c^{*}(\mathbb{N}^2)$
$C_c^{*}(\mathbb{N}^2)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 501-528
- Print publication:
- September 2023
-
- Article
- Export citation
Noncommutative rational Clark measures
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 27 July 2022, pp. 1393-1445
- Print publication:
- October 2023
-
- Article
- Export citation
Which states can be reached from a given state by unital completely positive maps?
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 05 July 2022, pp. 632-651
-
- Article
- Export citation
KMS states for generalized gauge actions on
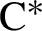 $\mathrm {C}^{\ast }$-algebras associated with self-similar sets
$\mathrm {C}^{\ast }$-algebras associated with self-similar sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 01 March 2022, pp. 1222-1238
- Print publication:
- April 2023
-
- Article
- Export citation
An
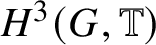 $H^{3}(G,{\mathbb T})$-valued index of symmetry-protected topological phases with on-site finite group symmetry for two-dimensional quantum spin systems
$H^{3}(G,{\mathbb T})$-valued index of symmetry-protected topological phases with on-site finite group symmetry for two-dimensional quantum spin systems
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 16 December 2021, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cocycles on groupoids arising from
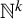 $\mathbb {N}^k$-actions
$\mathbb {N}^k$-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3325-3356
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariance of KMS states on graph C*-algebras under classical and quantum symmetry
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 20 September 2021, pp. 762-778
-
- Article
- Export citation
Regularity of simple nuclear real C*-algebras under tracial conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 139-147
-
- Article
- Export citation
The classification of symmetry protected topological phases of one-dimensional fermion systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 16 March 2021, e25
-
- Article
-
- You have access
- Open access
- Export citation
KMS states on the crossed product
 $C^*$-algebra of a homeomorphism
$C^*$-algebra of a homeomorphism
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 1373-1414
- Print publication:
- April 2022
-
- Article
- Export citation
INDUCTIVE LIMITS OF C*-ALGEBRAS AND COMPACT QUANTUM METRIC SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 27 March 2020, pp. 289-312
- Print publication:
- December 2021
-
- Article
- Export citation
Equilibrium states on higher-rank Toeplitz non-commutative solenoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 April 2019, pp. 2881-2912
- Print publication:
- November 2020
-
- Article
- Export citation
Heisenberg Modules over Quantum 2-tori are Metrized Quantum Vector Bundles
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 28 March 2019, pp. 1044-1081
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Unperforated Pairs of Operator Spaces and Hyperrigidity of Operator Systems
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 6 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1236-1260
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
An Equivariant Theory for the Bivariant Cuntz Semigroup
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 573-598
-
- Article
- Export citation
THE STATE-SPACE OF THE LATTICE OF ORTHOGONALLY CLOSED SUBSPACES
-
- Journal:
- Glasgow Mathematical Journal / Volume 47 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 31 January 2005, pp. 213-220
- Print publication:
- January 2005
-
- Article
-
- You have access
- Export citation
SIMULTANEOUS LIFTING FROM IRREDUCIBLE REPRESENTATIONS OF $C^*$-ALGEBRAS
-
- Journal:
- Glasgow Mathematical Journal / Volume 47 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 31 January 2005, pp. 195-204
- Print publication:
- January 2005
-
- Article
-
- You have access
- Export citation