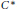Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Futamura, Hajime
Kataoka, Nobuhiro
and
Kishimoto, Akitaka
2003.
Type III representations and automorphisms of some separable nuclear C∗-algebras.
Journal of Functional Analysis,
Vol. 197,
Issue. 2,
p.
560.
Akemann, Charles
and
Weaver, Nik
2004.
Consistency of a counterexample to Naimark's problem.
Proceedings of the National Academy of Sciences,
Vol. 101,
Issue. 20,
p.
7522.
KISHIMOTO, AKITAKA
2004.
CORE SYMMETRIES OF A FLOW.
Reviews in Mathematical Physics,
Vol. 16,
Issue. 04,
p.
479.
Kishimoto, Akitaka
2006.
Operator Algebras.
p.
233.
Bratteli, Ola
Kishimoto, Akitaka
and
Robinson, Derek W.
2007.
Rohlin flows on the Cuntz algebraO∞.
Journal of Functional Analysis,
Vol. 248,
Issue. 2,
p.
472.
Buchholz, Detlev
Doplicher, Sergio
Morchio, Giovanni
Roberts, John E.
and
Strocchi, Franco
2007.
Rigorous Quantum Field Theory.
Vol. 251,
Issue. ,
p.
49.
Akemann, Charles
and
Weaver, Nik
2007.
Classically Normal Pure States.
Positivity,
Vol. 11,
Issue. 4,
p.
617.
AKEMANN, CHARLES
WASSERMANN, SIMON
and
WEAVER, NIK
2010.
PURE STATES ON FREE GROUP C*-ALGEBRAS.
Glasgow Mathematical Journal,
Vol. 52,
Issue. 1,
p.
151.
Christensen, Erik
Sinclair, Allan M.
Smith, Roger R.
White, Stuart A.
and
Winter, Wilhelm
2012.
Perturbations of nuclear C*-algebras.
Acta Mathematica,
Vol. 208,
Issue. 1,
p.
93.
Beltiţă, Daniel
and
Neeb, Karl‐Hermann
2012.
Schur–Weyl Theory for C*‐algebras.
Mathematische Nachrichten,
Vol. 285,
Issue. 10,
p.
1170.
Giordano, Thierry
and
Ng, Ping W.
2013.
Some consequences of von Neumann algebra uniqueness.
Journal of Functional Analysis,
Vol. 264,
Issue. 4,
p.
1112.
Kawahigashi, Yasuyuki
Ogata, Yoshiko
and
Størmer, Erling
2014.
Normal states of type III factors.
Pacific Journal of Mathematics,
Vol. 267,
Issue. 1,
p.
131.
Ando, Hiroshi
and
Kirchberg, Eberhard
2016.
Non-commutativity of the central sequence algebra for separable non-type I C*-algebras.
Journal of the London Mathematical Society,
Vol. 94,
Issue. 1,
p.
280.
Farah, Ilijas
and
Hirshberg, Ilan
2017.
Simple nuclear
C
*-algebras not isomorphic to their opposites
.
Proceedings of the National Academy of Sciences,
Vol. 114,
Issue. 24,
p.
6244.
Vaccaro, Andrea
2018.
Trace spaces of counterexamples to Naimark's problem.
Journal of Functional Analysis,
Vol. 275,
Issue. 10,
p.
2794.
2018.
C*-Algebras and their Automorphism Groups.
p.
291.
2018.
C*-Algebras and their Automorphism Groups.
p.
499.
Farah, Ilijas
2019.
Combinatorial Set Theory of C*-algebras.
p.
137.
Suzuki, Yuhei
2020.
On pathological properties of fixed point algebras in Kirchberg algebras.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 150,
Issue. 6,
p.
3087.
Vaccaro, Andrea
2020.
Corrigendum to “Trace spaces of counterexamples to Naimark's problem” [J. Funct. Anal. 275 (10) (2018) 2794–2816].
Journal of Functional Analysis,
Vol. 278,
Issue. 12,
p.
108458.