Refine search
Actions for selected content:
15 results
THE SET OF ELEMENTARY TENSORS IS WEAKLY CLOSED IN PROJECTIVE TENSOR PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 13 May 2024, pp. 336-343
- Print publication:
- April 2025
-
- Article
- Export citation
New characterizations of the unit vector basis of
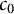 $c_0$ or
$c_0$ or 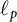 $ \ell _{p}$
$ \ell _{p}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 21 February 2023, pp. 1073-1083
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE EXISTENCE OF NON-NORM-ATTAINING OPERATORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 July 2021, pp. 1023-1035
- Print publication:
- May 2023
-
- Article
- Export citation
Uniformly factoring weakly compact operators and parametrised dualisation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 March 2021, e22
-
- Article
-
- You have access
- Open access
- Export citation
COMPATIBLE LOCALLY CONVEX TOPOLOGIES ON NORMED SPACES: CARDINALITY ASPECTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 139-145
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
On Super Weakly Compact Convex Sets and Representation of the Dual of the Normed Semigroup They Generate
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 272-282
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
Structure of the Set of Norm-attaining Functionals on Strictly Convex Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 2 / 01 June 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 302-310
- Print publication:
- 01 June 2011
-
- Article
-
- You have access
- Export citation
Right and Left Weak Approximation Properties in Banach Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 1 / 01 March 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 28-38
- Print publication:
- 01 March 2009
-
- Article
-
- You have access
- Export citation
ULTRAPOWERS AND SUBSPACES OF THE DUAL OF A BANACH SPACE
-
- Journal:
- Glasgow Mathematical Journal / Volume 45 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 10 September 2003, pp. 493-501
- Print publication:
- September 2003
-
- Article
-
- You have access
- Export citation
BANACH SPACES WHOSE ALGEBRAS OF OPERATORS ARE UNITARY: A HOLOMORPHIC APPROACH
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 2 / March 2003
- Published online by Cambridge University Press:
- 20 March 2003, pp. 218-224
- Print publication:
- March 2003
-
- Article
- Export citation
Nonlinear potentials in function spaces
-
- Journal:
- Nagoya Mathematical Journal / Volume 165 / March 2002
- Published online by Cambridge University Press:
- 22 January 2016, pp. 91-116
- Print publication:
- March 2002
-
- Article
-
- You have access
- Export citation
Extensions of Continuous and Lipschitz Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 2 / 01 June 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 208-217
- Print publication:
- 01 June 2000
-
- Article
-
- You have access
- Export citation
New Characterizations of the Reflexivity in Terms of the Set of Norm Attaining Functionals
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 3 / 01 September 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 279-289
- Print publication:
- 01 September 1998
-
- Article
-
- You have access
- Export citation
The weak drop property on closed convex sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 1 / February 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-130
- Print publication:
- February 1994
-
- Article
-
- You have access
- Export citation
On Basis Constants and Duality in Banach Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 22 / Issue 4 / 01 December 1979
- Published online by Cambridge University Press:
- 20 November 2018, pp. 459-465
- Print publication:
- 01 December 1979
-
- Article
-
- You have access
- Export citation

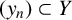
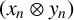
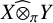
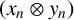
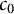
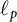
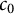
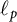
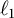
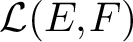
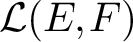
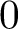
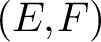
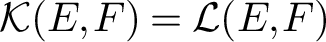
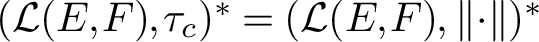
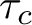
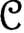
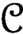
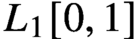
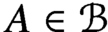
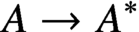
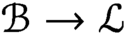

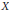
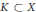
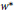
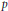
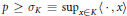
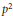
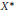
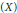
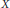
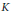
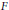
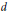
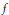
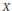


 has a much smaller (unconditional) basis constant than (
has a much smaller (unconditional) basis constant than (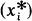 is
is 