Article contents
Extensions of Continuous and Lipschitz Functions
Published online by Cambridge University Press: 20 November 2018
Abstract
We show a result slightly more general than the following. Let  $K$ be a compact Hausdorff space,
$K$ be a compact Hausdorff space, 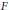 $F$ a closed subset of
$F$ a closed subset of  $K$ , and
$K$ , and 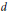 $d$ a lower semi-continuous metric on
$d$ a lower semi-continuous metric on  $K$ . Then each continuous function
$K$ . Then each continuous function 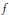 $f$ on
$f$ on 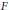 $F$ which is Lipschitz in
$F$ which is Lipschitz in 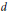 $d$ admits a continuous extension on
$d$ admits a continuous extension on  $K$ which is Lipschitz in
$K$ which is Lipschitz in 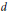 $d$ . The extension has the same supremum norm and the same Lipschitz constant.
$d$ . The extension has the same supremum norm and the same Lipschitz constant.
As a corollary we get that a Banach space 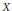 $X$ is reflexive if and only if each bounded, weakly continuous and norm Lipschitz function defined on a weakly closed subset of
$X$ is reflexive if and only if each bounded, weakly continuous and norm Lipschitz function defined on a weakly closed subset of 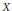 $X$ admits a weakly continuous, norm Lipschitz extension defined on the entire space
$X$ admits a weakly continuous, norm Lipschitz extension defined on the entire space 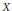 $X$ .
$X$ .
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2000
References
- 12
- Cited by

