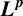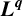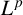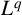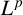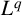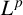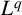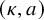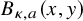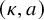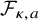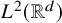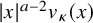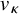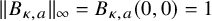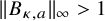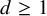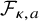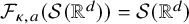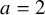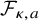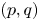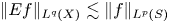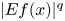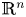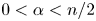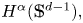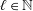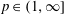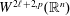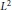Refine search
Actions for selected content:
26 results
A phase-space approach to weighted Fourier extension inequalities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 November 2025, e181
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trigonometric convexity of the multidimensional indicator
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 05 January 2024, pp. 384-399
- Print publication:
- April 2025
-
- Article
- Export citation
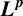 $\boldsymbol {L}^{\boldsymbol {p}}$–
$\boldsymbol {L}^{\boldsymbol {p}}$–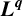 $\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
$\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 18 October 2023, pp. 375-395
- Print publication:
- December 2023
-
- Article
- Export citation
On the kernel of the
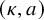 $(\kappa ,a)$-Generalized fourier transform
$(\kappa ,a)$-Generalized fourier transform
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 August 2023, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fourier restriction in low fractal dimensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 373-407
-
- Article
- Export citation
Eigenfunctions of the Fourier transform with specified zeros
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 329-367
- Print publication:
- September 2021
-
- Article
- Export citation
The Fourier extension operator of distributions in Sobolev spaces of the sphere and the Helmholtz equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. 1768-1789
- Print publication:
- December 2021
-
- Article
- Export citation
FKN theorem for the multislice, with applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 18 October 2019, pp. 200-212
-
- Article
- Export citation
A comparison principle for convolution measures with applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 28 June 2019, pp. 307-322
- Print publication:
- September 2020
-
- Article
- Export citation
Explicit Salem sets, Fourier restriction, and metric Diophantine approximation in the p-adic numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1265-1288
- Print publication:
- June 2020
-
- Article
- Export citation
Pointwise Characterizations of Even Order Sobolev Spaces via Derivatives of Ball Averages
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 681-699
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Uncertainty Principles on Weighted Spheres, Balls, and Simplexes
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 1 / 01 March 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 62-72
- Print publication:
- 01 March 2016
-
- Article
-
- You have access
- Export citation
BOUNDS ON PRICES FOR ASIAN OPTIONS VIAFOURIER METHODS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 3 / January 2016
- Published online by Cambridge University Press:
- 19 February 2016, pp. 299-318
-
- Article
-
- You have access
- Export citation
Restricting Fourier Transforms of Measures to Curves in ℝ2
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 326-336
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
Measures with Fourier Transforms in L 2 of a Half-space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 1 / 01 March 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 172-179
- Print publication:
- 01 March 2011
-
- Article
-
- You have access
- Export citation
RESTRICTION OF FOURIER TRANSFORMS TO CURVES II: SOME CLASSES WITH VANISHING TORSION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 1-28
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
A NOTE ON LOCALISED WEIGHTED INEQUALITIES FOR THE EXTENSION OPERATOR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 289-299
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Multidimensional Hausdorff operators on the real Hardy space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 79-86
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
On Pointwise Estimates of Positive Definite Functions With Given Support
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 2 / 01 April 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 401-418
- Print publication:
- 01 April 2006
-
- Article
-
- You have access
- Export citation
UNCERTAINTY PRINCIPLES FOR THE AMBIGUITY FUNCTION
-
- Journal:
- Journal of the London Mathematical Society / Volume 72 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 08 December 2005, pp. 717-730
- Print publication:
- December 2005
-
- Article
- Export citation