Article contents
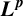 $\boldsymbol {L}^{\boldsymbol {p}}$–
$\boldsymbol {L}^{\boldsymbol {p}}$–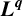 $\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
$\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
Published online by Cambridge University Press: 18 October 2023
Abstract
The main purpose of this paper is to prove Hörmander’s 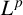 $L^p$–
$L^p$–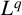 $L^q$ boundedness of Fourier multipliers on commutative hypergroups. We carry out this objective by establishing the Paley inequality and Hausdorff–Young–Paley inequality for commutative hypergroups. We show the
$L^q$ boundedness of Fourier multipliers on commutative hypergroups. We carry out this objective by establishing the Paley inequality and Hausdorff–Young–Paley inequality for commutative hypergroups. We show the 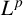 $L^p$–
$L^p$–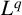 $L^q$ boundedness of the spectral multipliers for the generalised radial Laplacian by examining our results on Chébli–Trimèche hypergroups. As a consequence, we obtain embedding theorems and time asymptotics for the
$L^q$ boundedness of the spectral multipliers for the generalised radial Laplacian by examining our results on Chébli–Trimèche hypergroups. As a consequence, we obtain embedding theorems and time asymptotics for the 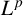 $L^p$–
$L^p$–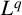 $L^q$ norms of the heat kernel for generalised radial Laplacian.
$L^q$ norms of the heat kernel for generalised radial Laplacian.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 115 , Issue 3 , December 2023 , pp. 375 - 395
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Ji Li
The authors are supported by FWO Odysseus 1 Grant G.0H94.18N: Analysis and Partial Differential Equations, the Methusalem programme of the Ghent University Special Research Fund (BOF) (Grant number 01M01021) and by FWO Senior Research Grant G011522N. MR is also supported by the EPSRC Grant EP/R003025/2 and by the FWO Grant G022821N.
References
- 3
- Cited by


