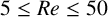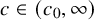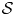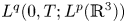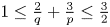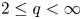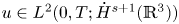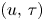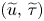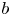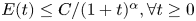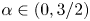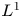Refine search
Actions for selected content:
56 results
Well-posedness of Naiver–Stokes equations in logarithmic Q spaces covering
 $BMO^{-1}$ and its fractional counterpart
$BMO^{-1}$ and its fractional counterpart
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3D Navier–Stokes–Voigt equations with damping and double delays on unbounded domains: Well-posedness, pullback attractors, and limit measures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1-39
-
- Article
- Export citation
Smooth imploding solutions for 3D compressible fluids
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FURTHER ACCURACY VERIFICATION OF A 2D ADAPTIVE MESH REFINEMENT METHOD USING STEADY FLOW PAST A SQUARE CYLINDER
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 19 November 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Axisymmetric Incompressible Viscous Plasmas: Global Well-Posedness and Asymptotics
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 September 2024, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modelling of the fluid flow in a thin domain with injection through permeable boundary
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 776-796
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the reconstruction of unknown driving forces from low-mode observations in the 2D Navier–Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-24
-
- Article
- Export citation
A collision result for both non-Newtonian and heat conducting Newtonian compressible fluids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1631-1645
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The non-autonomous Navier–Stokes–Brinkman–Forchheimer equation with Dirichlet boundary conditions: dissipativity, regularity, and attractors
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 September 2023, pp. 352-393
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
OPTIMAL GEVREY STABILITY OF HYDROSTATIC APPROXIMATION FOR THE NAVIER-STOKES EQUATIONS IN A THIN DOMAIN
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 September 2023, pp. 1521-1566
- Print publication:
- July 2024
-
- Article
- Export citation
Fractal dimension of potential singular points set in the Navier–Stokes equations under supercritical regularity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 727-745
- Print publication:
- June 2024
-
- Article
- Export citation
Vanishing limit for the three-dimensional incompressible Phan-Thien–Tanner system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 673-698
- Print publication:
- June 2024
-
- Article
- Export citation
Global existence and large time behaviour for the pressureless Euler–Naver–Stokes system in ℝ3
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 22 February 2023, pp. 328-352
- Print publication:
- February 2024
-
- Article
- Export citation
Zero-electron-mass limit of the compressible Navier–Stokes–Poisson equations with well/ill-prepared initial data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 1439-1466
- Print publication:
- October 2023
-
- Article
- Export citation
The stability analysis of a 2D Keller–Segel–Navier–Stokes system in fast signal diffusion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 31 March 2022, pp. 160-209
-
- Article
-
- You have access
- HTML
- Export citation
Decay of weak solutions to Vlasov equation coupled with a shear thickening fluid
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 167-176
- Print publication:
- February 2023
-
- Article
- Export citation
Global well-posedness and decay estimates for three-dimensional compressible Navier–Stokes–Allen–Cahn systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 1291-1322
- Print publication:
- October 2022
-
- Article
- Export citation
Decay properties for the incompressible Navier-Stokes flows in a half space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 1509-1532
- Print publication:
- December 2022
-
- Article
- Export citation
Well-posedness of the free surface problem on a Newtonian fluid between cylinders rotating at different speeds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 1251-1276
- Print publication:
- October 2022
-
- Article
- Export citation
On regularity properties of a surface growth model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 09 March 2021, pp. 1869-1892
- Print publication:
- December 2021
-
- Article
- Export citation