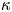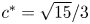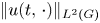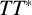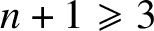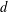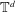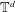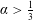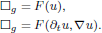Refine search
Actions for selected content:
43 results
Bifurcation of the travelling wave solutions in a perturbed (1 + 1)-dimensional dispersive long wave equation via a geometric approach
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-28
-
- Article
- Export citation
Dispersive and Strichartz estimates for 3D wave equation with a Laguerre potential
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 863-890
- Print publication:
- June 2025
-
- Article
- Export citation
Estimates for the nonlinear viscoelastic damped wave equation on compact Lie groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 810-829
- Print publication:
- June 2024
-
- Article
- Export citation
STRICHARTZ ESTIMATES FOR THE WAVE EQUATION INSIDE CYLINDRICAL CONVEX DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 August 2022, pp. 304-312
- Print publication:
- April 2023
-
- Article
- Export citation
The zero mass problem for Klein-Gordon equations: quadratic null interactions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 20 May 2022, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inverse problems for nonlinear hyperbolic equations with disjoint sources and receivers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 02 November 2021, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scattering for critical wave equations with variable coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 298-316
-
- Article
- Export citation
Uniform convergence in von Neumann’s ergodic theorem in the absence of a spectral gap
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 1601-1611
- Print publication:
- June 2021
-
- Article
- Export citation
LONG TIME BEHAVIOR OF THE SOLUTIONS OF NLW ON THE
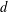 $d$-DIMENSIONAL TORUS
$d$-DIMENSIONAL TORUS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 March 2020, e12
-
- Article
-
- You have access
- Open access
- Export citation
Pointwise Convergence of Solutions to the Schrödinger Equation on Manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 983-995
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Lifespan of solutions to wave equations in de Sitter spacetime
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 10 April 2018, pp. 1313-1330
- Print publication:
- December 2018
-
- Article
- Export citation
LOCAL DECAY FOR THE DAMPED WAVE EQUATION IN THE ENERGY SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 01 April 2016, pp. 509-540
- Print publication:
- June 2018
-
- Article
- Export citation
Development of a Combined Compact Difference Scheme to Simulate Soliton Collision in a Shallow Water Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 603-631
- Print publication:
- March 2016
-
- Article
- Export citation
SOME SHARP BILINEAR SPACE–TIME ESTIMATES FOR THE WAVE EQUATION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 07 March 2016, pp. 719-737
- Print publication:
- 2016
-
- Article
- Export citation
Lp -type pullback attractors for a semilinear heat equation on time-varying domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 1029-1052
- Print publication:
- October 2015
-
- Article
- Export citation
A Multilevel Numerical Approach with Application in Time-Domain Electromagnetics
-
- Journal:
- Communications in Computational Physics / Volume 17 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 24 March 2015, pp. 703-720
- Print publication:
- March 2015
-
- Article
- Export citation
Simulation of Earthquake Rupture Dynamics in Complex Geometries Using Coupled Finite Difference and Finite Volume Methods
-
- Journal:
- Communications in Computational Physics / Volume 17 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 22 January 2015, pp. 337-370
- Print publication:
- February 2015
-
- Article
- Export citation
A Flexible Boundary Procedure for Hyperbolic Problems: Multiple Penalty Terms Applied in a Domain
-
- Journal:
- Communications in Computational Physics / Volume 16 / Issue 2 / August 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 345-358
- Print publication:
- August 2014
-
- Article
- Export citation
On the existence of global weak solutions to an integrable two-component Camassa–Holm shallow-water system
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 755-775
-
- Article
-
- You have access
- Export citation
NONLINEAR WAVE EQUATIONS AND REACTION–DIFFUSION EQUATIONS WITH SEVERAL NONLINEAR SOURCE TERMS OF DIFFERENT SIGNS AT HIGH ENERGY LEVEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 3 / January 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 153-170
-
- Article
-
- You have access
- Export citation