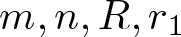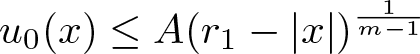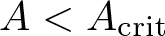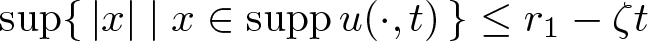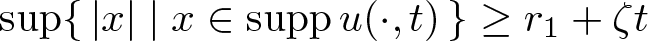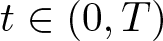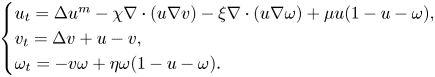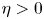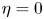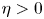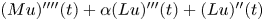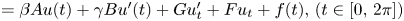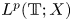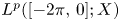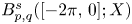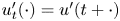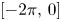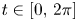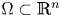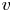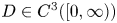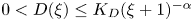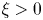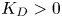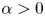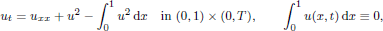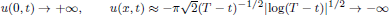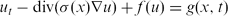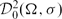Refine search
Actions for selected content:
28 results
Shrinking vs. expanding: the evolution of spatial support in degenerate Keller–Segel systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 September 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The roles of nonlinear diffusion, haptotaxis and ECM remodelling in determining the global solvability of a cancer invasion model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-32
-
- Article
- Export citation
Eternal solutions to a porous medium equation with strong non-homogeneous absorption. Part I: radially non-increasing profiles
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1998-2019
- Print publication:
- December 2025
-
- Article
- Export citation
Periodic solutions of four-order degenerate differential equations with finite delay in vector-valued function spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 September 2023, pp. 395-412
- Print publication:
- April 2025
-
- Article
- Export citation
Finite-time blow-up in a repulsive chemotaxis-consumption system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 1150-1166
- Print publication:
- August 2023
-
- Article
- Export citation
Existence and uniqueness of solutions to a flow and transport problem with degenerating coefficients
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 55-76
-
- Article
-
- You have access
- HTML
- Export citation
On travelling wave solutions of a model of a liquid film flowing down a fibre
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 12 August 2021, pp. 864-893
-
- Article
- Export citation
Degenerate equations in a diffusion–precipitation model for clogging porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 1050-1069
-
- Article
-
- You have access
- Open access
- Export citation
Global minimisers for anisotropic attractive–repulsive interactions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 22 October 2019, pp. 854-870
-
- Article
- Export citation
Uniqueness and time oscillating behaviour of finite points blow-up solutions of the fast diffusion equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 2849-2870
- Print publication:
- December 2020
-
- Article
- Export citation
Evolution of interfaces for the nonlinear parabolic p-Laplacian-type reaction-diffusion equations. II. Fast diffusion vs. absorption
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 18 March 2019, pp. 385-406
-
- Article
- Export citation
Complete quenching phenomenon and instantaneous shrinking of support of solutions of degenerate parabolic equations with nonlinear singular absorption
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1323-1346
- Print publication:
- October 2019
-
- Article
- Export citation
Simulation of multiphase porous media flows with minimising movement and finite volume schemes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 1123-1152
-
- Article
- Export citation
Time adaptive numerical solution of a highly non-linear degenerate cross-diffusion system arising in multi-species biofilm modelling
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 10 September 2018, pp. 1035-1061
-
- Article
-
- You have access
- Export citation
Convergence of Monotone Schemes for Conservation Laws with Zero-Flux Boundary Conditions
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 17 January 2017, pp. 515-542
- Print publication:
- June 2017
-
- Article
- Export citation
The interface dynamics of a surfactant drop on a thin viscous film†
-
- Journal:
- European Journal of Applied Mathematics / Volume 28 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 08 November 2016, pp. 656-686
-
- Article
- Export citation
Global blow-up for a semilinear heat equation on a subspace
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 24 August 2015, pp. 893-923
- Print publication:
- October 2015
-
- Article
- Export citation
A Diffusively Corrected Multiclass Lighthill-Whitham-Richards Traffic Model with Anticipation Lengths and Reaction Times
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 5 / Issue 5 / October 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 728-758
- Print publication:
- October 2013
-
- Article
- Export citation
Explorations and Expectations of Equidistribution Adaptations for Nonlinear Quenching Problems
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 5 / Issue 4 / August 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 407-422
- Print publication:
- August 2013
-
- Article
- Export citation
REGULARITY AND FRACTAL DIMENSION OF PULLBACK ATTRACTORS FOR A NON-AUTONOMOUS SEMILINEAR DEGENERATE PARABOLIC EQUATION
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 431-448
- Print publication:
- May 2013
-
- Article
-
- You have access
- Export citation